Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T22:18:28.407Z Has data issue: false hasContentIssue false
  • English
  • Français

On Semi-Primary Self-Injective Rings and Faith's Quasi-Frobenius Conjecture

Part of: Local rings and generalizations Modules, bimodules and ideals

Published online by Cambridge University Press:  10 December 2014

M. C. Iovanov
M. C. Iovanov*
Affiliation:
Department of Mathematics, University of Iowa, 14 MacLean Hall, Iowa City, Iowa 52242-1419, USA, ([email protected]) Facultatea de Matematica, University of Bucharest, Str. Academiei 14, Sector 1, Bucharest 010014, Romania
Get access Rights & Permissions [Opens in a new window]

Abstract

A long-standing conjecture of Faith in ring theory states that a left self-injective semi-primary ring A is necessarily a quasi-Frobenius ring. We propose a new method for approaching this conjecture, and prove it under some mild conditions; we show that if the simple A-modules are at most countably generated over a subring of the centre of A, then the conjecture holds. Also, the conjecture holds for 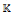algebras A over sufficiently large fields, i.e. if the cardinality of 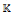is larger than the dimension of the simple A-modules (or of A/Jac(A)). This effectively proves the conjecture in many situations, and we obtain several previously known results on this problem as a consequence.

Keywords

quasi-Frobenius ringsQF ringsFaith conjectureself-injective ring

MSC classification

Primary: 16D50: Injective modules, self-injective rings 16L60: Quasi-Frobenius rings
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 1 , February 2015 , pp. 219 - 229
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anderson, F. W. and Fuller, K., Rings and categories of modules, Graduate Texts in Mathematics (Springer, 1974).Google Scholar
2.Ara, P. and Park, J. K., On continuous semiprimary rings, Commun. Alg. 19(7) (1991), 1945–1957.Google Scholar
3.Ara, P., Nicholson, W. K. and Yousif, M. F., A look at the Faith conjecture, Glasgow Math. J. 42 (2001), 391–404.CrossRefGoogle Scholar
4.Clark, J. and Huynh, D. V., A note on perfect left self-injective rings, Q. J. Math. 45 (1994), 13–17.Google Scholar
5.Clark, J. and Smith, P. F., On semi-artinian modules and injectivity conditions, Proc. Edinb. Math. Soc. 39 (1996), 263–270.CrossRefGoogle Scholar
6.Faith, C., Algebra II: ring theory, Volume 191 (Springer, 1976).Google Scholar
7.Faith, C. and van Huynh, D., When self-injective rings are QF: a report on a problem, J. Alg. Appl. 1 (1) (2002), 75–105.Google Scholar
8.Fichtenholz, G. M. and Kantorovich, L. V., Sur les operations lineares dans l'espace de fonctions bornees, Studia Math. 5 (1935), 69–98.Google Scholar
9.Haim, M., Iovanov, M. C. and Torrecillas, B., On two conjectures of Faith, J. Alg. 367 (2012), 166–175.CrossRefGoogle Scholar
10.Iovanov, M. C., Semiprimary selfinjective algebras with at most countable dimensional Jacobson quotient are QF, preprint (arXiv:1111.2901, 2011).Google Scholar
11.Jacobson, N., Lectures in abstract algebra: linear algebra, Volume 2 (Springer, 1951).Google Scholar
12.Kato, T., Self-injective rings, Tohoku Math. J. 19(4) (1967), 485–495.Google Scholar
13.Koike, K., On self-injective semiprimary rings, Commun. Alg. 28 (2000), 4303–4319.CrossRefGoogle Scholar
14.Lam, T.-Y., Lectures on modules and rings, Graduate Texts in Mathematics, Issue 189 (Springer, 1999).CrossRefGoogle Scholar
15.Lawrence, J., A countable self-injective ring is quasi-Frobenius, Proc. Am. Math. Soc. 65 (1977), 217–220 (erratum, Proc. Am. Math. Soc. 73(1) (1979), 140).Google Scholar
16.Nicholson, W. K. and Yousif, M. F., Mininjective rings, J. Alg. 187(2) (1997), 548–578.Google Scholar
17.Nicholson, W. K. and Yousif, M. F., On finitely embedded rings, Commun. Alg. 28 (2000), 5311–5315.Google Scholar
18.Nicholson, W. K. and Yousif, M. F., Quasi-Frobenius rings (Cambridge University Press, 2003).Google Scholar
19.Oshiro, K., On the Faith conjecture, in Contemporary ring theory 2011: proceedings of the sixth China-Japan-Korea international conference on ring theory (ed. Kim, J. Y., Huh, C. and Lee, Y.) (World Scientific, 2012).Google Scholar
20.Osofsky, B., A generalization of quasi-Frobenius rings, J. Alg. 4 (1966), 373–387.Google Scholar
21.Xue, W., A note on perfect self-injective rings, Commun. Alg. 24 (1996), 749–755.CrossRefGoogle Scholar