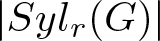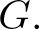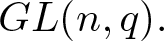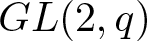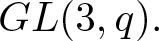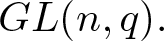1. Introduction
The significance of Steinberg characters to the study of finite groups of Lie type was well established by Curtis, Humphreys and Steinberg in [Reference Curtis3, Reference Humphreys8, Reference Steinberg16] and [Reference Steinberg17]. Motivated by the intrinsic property of the Steinberg character, Feit introduced the notion of an r-Steinberg character for any finite group G and for any prime divisor r of the order of G (see [Reference Feit5]). Recall that an element of a group is called r-regular if its order is co-prime to ![]() $r.$ An irreducible character of G is said to be r-Steinberg if each r-regular element, say
$r.$ An irreducible character of G is said to be r-Steinberg if each r-regular element, say ![]() $\displaystyle g,$ of G takes the value
$\displaystyle g,$ of G takes the value ![]() $\displaystyle \pm{|C_G(g)|_r}$ on it. Here
$\displaystyle \pm{|C_G(g)|_r}$ on it. Here ![]() $|C_G(g)|_r$ is the highest power of r dividing the order of the centralizer
$|C_G(g)|_r$ is the highest power of r dividing the order of the centralizer ![]() $C_G(g)$ of g in
$C_G(g)$ of g in ![]() $G.$
$G.$
Feit conjectured [Reference Feit5] that if a finite simple group has an r-Steinberg character, then it is isomorphic to a simple group of Lie type in characteristic r. Darafsheh obtained an affirmative answer to this conjecture for the alternating and projective special linear groups (see [Reference Darafsheh4]). Later, Tiep [Reference Tiep18] extended the study to the rest of the finite simple groups and gave a positive answer.
In the last decade, several variants of r-Steinberg character have emerged as an important tool for studying the structure of finite groups through their characters (see [Reference Pellegrini and Zalesski13]). One of the variants of r-Steinberg character is an r-vanishing character which is an irreducible character that vanishes on all the r-singular elements of the group. Note here that an element of a group is called r-singular if its order is divisible by r. In particular, if the degree of an r-vanishing character is ![]() $|Syl_r(G)|,$ where
$|Syl_r(G)|,$ where ![]() $\displaystyle |Syl_r(G)|$ is the order of the Sylow r-subgroup of
$\displaystyle |Syl_r(G)|$ is the order of the Sylow r-subgroup of ![]() $G,$ then the character is said to be Steinberg-like. In [Reference Malle and Zalesski9], Malle and Zalesski obtained a classification of the Steinberg-like characters of all finite simple groups.
$G,$ then the character is said to be Steinberg-like. In [Reference Malle and Zalesski9], Malle and Zalesski obtained a classification of the Steinberg-like characters of all finite simple groups.
Recently, Paul and Singla [Reference Paul and Singla12] introduced the notion of a quasi r-Steinberg character and a weak r-Steinberg character:
Definition 1.1. Let G be a finite group and r be a prime dividing its order. An irreducible character of G is said to be quasi r-Steinberg if it takes non-zero value on every r-regular element of ![]() $\displaystyle G.$ Further, a quasi r-Steinberg character which is Steinberg-like is said to be a weak r-Steinberg character.
$\displaystyle G.$ Further, a quasi r-Steinberg character which is Steinberg-like is said to be a weak r-Steinberg character.
It follows that the r-Steinberg and the weak r-Steinberg characters are quasi r-Steinberg, but the converse need not be true. The above two variants of r-Steinberg characters were introduced to answer a question posed by Dipendra Prasad that asked whether the existence of a weak r-Steinberg character of a finite group G implies that G is a group of Lie type. It is well known that every finite group of Lie type has a r-Steinberg character for a prime r. Hence if a group does not have a nonlinear quasi r-Steinberg character, then it cannot be a finite group of Lie type of characteristic r. Therefore, one naturally requires the classification of quasi r-Steinberg characters of any finite group G.
In [Reference Paul and Singla12], the authors classified all the quasi r-Steinberg characters of symmetric and alternating groups and their double covers. A classification of the quasi r-Steinberg characters for the complex reflection groups has recently been done in [Reference Mishra, Paul and Singla11].
In the present article, we study the quasi and weak r-Steinberg characters of the general linear group ![]() $GL(n,q)$ over a finite field Fq, where q is a power of prime p. Since every linear character of G is quasi r-Steinberg for any prime divisor r of
$GL(n,q)$ over a finite field Fq, where q is a power of prime p. Since every linear character of G is quasi r-Steinberg for any prime divisor r of ![]() $|G|,$ one aims at the classification of the nonlinear quasi r-Steinberg characters of
$|G|,$ one aims at the classification of the nonlinear quasi r-Steinberg characters of ![]() $G.$ The paper is divided into six sections. In the second section, we introduce the notation which we follow throughout the article. In the third section, we classify the quasi r-Steinberg cuspidal characters of
$G.$ The paper is divided into six sections. In the second section, we introduce the notation which we follow throughout the article. In the third section, we classify the quasi r-Steinberg cuspidal characters of ![]() $GL(n,q)$ and the following is the first main result of the paper:
$GL(n,q)$ and the following is the first main result of the paper:
Theorem 1.2. Let ![]() $\displaystyle n \geq 2$ be an integer and
$\displaystyle n \geq 2$ be an integer and ![]() $\displaystyle r$ be a prime divisor of the order of
$\displaystyle r$ be a prime divisor of the order of ![]() $\displaystyle GL(n,q).$ Then a cuspidal character of
$\displaystyle GL(n,q).$ Then a cuspidal character of ![]() $\displaystyle GL(n,q)$ is quasi r-Steinberg if and only if one of the following holds:
$\displaystyle GL(n,q)$ is quasi r-Steinberg if and only if one of the following holds:
1. n = 2 and
 $\displaystyle q = r^{\beta}+1,$ for some
$\displaystyle q = r^{\beta}+1,$ for some  $\displaystyle \beta \in \mathbb{N}.$
$\displaystyle \beta \in \mathbb{N}.$2. n = 3 and
 $q = 3,$ when r = 2.
$q = 3,$ when r = 2.3. n = 3 and
 $q = 2,$ when r = 3.
$q = 2,$ when r = 3.
In the fourth and the penultimate section, we characterize the quasi r-Steinberg characters of ![]() $GL(2,q)$ and
$GL(2,q)$ and ![]() $GL(3,q),$ respectively.
$GL(3,q),$ respectively.
Let χl be a character of ![]() $\displaystyle F_q^{*}$ indexed by
$\displaystyle F_q^{*}$ indexed by ![]() $\displaystyle l \in \{0, 1, \ldots, (q-2)\}$. Further, let
$\displaystyle l \in \{0, 1, \ldots, (q-2)\}$. Further, let  $\chi_k^{(1)}$ denote a linear and χt denote a cuspidal character of
$\chi_k^{(1)}$ denote a linear and χt denote a cuspidal character of ![]() $GL(2,q)$ indexed by some
$GL(2,q)$ indexed by some ![]() $\displaystyle k \in \{0, 1, \ldots, (q-2)\}$ and
$\displaystyle k \in \{0, 1, \ldots, (q-2)\}$ and ![]() $\displaystyle t \in \{1, 2, \ldots, (q^2-1)\}.$ Assume that
$\displaystyle t \in \{1, 2, \ldots, (q^2-1)\}.$ Assume that ![]() $L_{(2,1)}$ denotes the standard Levi complement of the standard parabolic subgroup (say
$L_{(2,1)}$ denotes the standard Levi complement of the standard parabolic subgroup (say ![]() $P_{(2,1)}$) of
$P_{(2,1)}$) of ![]() $GL(3,q).$ We denote the characters of
$GL(3,q).$ We denote the characters of ![]() $GL(3,q)$ obtained by parabolic induction of the irreducible characters
$GL(3,q)$ obtained by parabolic induction of the irreducible characters  $\chi_k^{(1)} \bigotimes \chi_l$ and
$\chi_k^{(1)} \bigotimes \chi_l$ and ![]() $\chi_t \bigotimes \chi_l$ of
$\chi_t \bigotimes \chi_l$ of ![]() $L_{(2,1)}$ by
$L_{(2,1)}$ by  $\displaystyle \theta_{k,l}^{(4)}$ and
$\displaystyle \theta_{k,l}^{(4)}$ and  $\displaystyle \theta_{t,l}^{(7)}$, respectively. The following is the second main result of the paper, which gives a classification of the weak r-Steinberg characters of
$\displaystyle \theta_{t,l}^{(7)}$, respectively. The following is the second main result of the paper, which gives a classification of the weak r-Steinberg characters of ![]() $GL(n,q)$.
$GL(n,q)$.
Theorem 1.3. Let ![]() $\displaystyle r$ be a prime divisor of
$\displaystyle r$ be a prime divisor of ![]() $|GL(n,q)|$ different from
$|GL(n,q)|$ different from ![]() $p.$ Then an irreducible character χ of
$p.$ Then an irreducible character χ of ![]() $GL(n,q)$ is weak r-Steinberg if and only if one of the following holds:
$GL(n,q)$ is weak r-Steinberg if and only if one of the following holds:
1. χ is a parabolically induced character of
 $GL(2,q)$ where
$GL(2,q)$ where  $(q+1)$ is an r-power, for some odd prime r.
$(q+1)$ is an r-power, for some odd prime r.2.
 $\displaystyle \chi$ is a character of type
$\displaystyle \chi$ is a character of type  $ \displaystyle \theta_{k,l}^{(4)}$ of
$ \displaystyle \theta_{k,l}^{(4)}$ of  $GL(3,q),$ where
$GL(3,q),$ where• If q is odd, then
 $(1+q+q^2)$ is an r-power,
$(1+q+q^2)$ is an r-power,  $3 \nmid (q-1)$ and
$3 \nmid (q-1)$ and  $(l-k)$ is not invertible in
$(l-k)$ is not invertible in  $\displaystyle \mathbb{Z}_{q-1}.$
$\displaystyle \mathbb{Z}_{q-1}.$• If q is even, then
 $(1+q+q^2)$ is an r-power.
$(1+q+q^2)$ is an r-power.
3.
 $\displaystyle \chi$ is the character
$\displaystyle \chi$ is the character  $ \theta_{t,l}^{(7)}$ of
$ \theta_{t,l}^{(7)}$ of  $GL(3,2)$ and r = 7.
$GL(3,2)$ and r = 7.4. χ is a cuspidal character of
 $GL(3,2)$ and r = 3.
$GL(3,2)$ and r = 3.
2. Notation and preliminaries
For a finite group ![]() $G,$ we denote the set of its irreducible characters by
$G,$ we denote the set of its irreducible characters by ![]() $Irr(G).$ We say that the conjugacy class
$Irr(G).$ We say that the conjugacy class ![]() $[g]$ of an element g of
$[g]$ of an element g of ![]() $GL(n,q)$ is primary if its characteristic polynomial has a unique irreducible factor. Further, g is said to be irreducible if its characteristic polynomial over Fq is irreducible of degree n. For any
$GL(n,q)$ is primary if its characteristic polynomial has a unique irreducible factor. Further, g is said to be irreducible if its characteristic polynomial over Fq is irreducible of degree n. For any ![]() $\displaystyle n \geq 1,$ assume that
$\displaystyle n \geq 1,$ assume that ![]() $\displaystyle F_{q^n}^{*} = \langle \epsilon_n \rangle.$ Then we denote the irreducible element
$\displaystyle F_{q^n}^{*} = \langle \epsilon_n \rangle.$ Then we denote the irreducible element  $diag(\epsilon_n, \epsilon_n^q, \ldots, \epsilon_n^{q^{n-1}})$ of
$diag(\epsilon_n, \epsilon_n^q, \ldots, \epsilon_n^{q^{n-1}})$ of ![]() $GL(n,q)$ by
$GL(n,q)$ by ![]() $\displaystyle E_n$. Let
$\displaystyle E_n$. Let ![]() $\displaystyle \hat \ : \ F_{q^n}^{*} \rightarrow \mathbb{C}^{*}$ be the homomorphism defined by the rule
$\displaystyle \hat \ : \ F_{q^n}^{*} \rightarrow \mathbb{C}^{*}$ be the homomorphism defined by the rule  $\displaystyle \hat (\epsilon_{n}^{s}) = \hat{\epsilon_{n}^{s}} = e^{s \frac{2 \pi i}{q^n-1}},$ where
$\displaystyle \hat (\epsilon_{n}^{s}) = \hat{\epsilon_{n}^{s}} = e^{s \frac{2 \pi i}{q^n-1}},$ where ![]() $\displaystyle 0 \leq s \leq (q^n-2).$
$\displaystyle 0 \leq s \leq (q^n-2).$
The character tables of ![]() $\displaystyle GL(2,q)$ and
$\displaystyle GL(2,q)$ and ![]() $\displaystyle GL(3,q)$ can be found in [Reference Steinberg15] and are also included in Appendix of this paper. We follow [Reference Basheer1] for the notation of the conjugacy classes and the characters of these groups. For any partition
$\displaystyle GL(3,q)$ can be found in [Reference Steinberg15] and are also included in Appendix of this paper. We follow [Reference Basheer1] for the notation of the conjugacy classes and the characters of these groups. For any partition ![]() $\displaystyle \lambda = (\lambda_1, \lambda_2, \ldots, \lambda_m)$ of
$\displaystyle \lambda = (\lambda_1, \lambda_2, \ldots, \lambda_m)$ of ![]() $n,$ let Pλ denote the standard parabolic subgroup of
$n,$ let Pλ denote the standard parabolic subgroup of ![]() $GL(n,q).$ The unipotent radical and the Levi complement of Pλ are denoted by Uλ and
$GL(n,q).$ The unipotent radical and the Levi complement of Pλ are denoted by Uλ and ![]() $L_{\lambda},$ respectively. Assume that for any
$L_{\lambda},$ respectively. Assume that for any ![]() $\displaystyle 1 \leq i \leq m,$
$\displaystyle 1 \leq i \leq m,$ ![]() $\displaystyle \chi_{\lambda_i} \in Irr(GL(\lambda_i, q)).$ An irreducible character of
$\displaystyle \chi_{\lambda_i} \in Irr(GL(\lambda_i, q)).$ An irreducible character of ![]() $GL(n,q)$ obtained by parabolic induction of the character of
$GL(n,q)$ obtained by parabolic induction of the character of ![]() $\displaystyle P_{\lambda}$ lifted from
$\displaystyle P_{\lambda}$ lifted from  $\displaystyle \bigotimes_{i=1}^{m} \chi_{\lambda_i} \in Irr(L_{\lambda})$ is called a parabolically induced character and is denoted by
$\displaystyle \bigotimes_{i=1}^{m} \chi_{\lambda_i} \in Irr(L_{\lambda})$ is called a parabolically induced character and is denoted by  $\displaystyle \bigodot_{i=1}^{m} \chi_{\lambda_i}.$
$\displaystyle \bigodot_{i=1}^{m} \chi_{\lambda_i}.$
We first list the types of the conjugacy classes of ![]() $GL(2,q)$ and
$GL(2,q)$ and ![]() $GL(3,q)$. We denote by
$GL(3,q)$. We denote by ![]() $C^{(1)}$ and
$C^{(1)}$ and ![]() $C^{(2)}$ the types of conjugacy classes of the elements of
$C^{(2)}$ the types of conjugacy classes of the elements of ![]() $GL(2,q)$ whose characteristic polynomial is
$GL(2,q)$ whose characteristic polynomial is ![]() $\displaystyle (x-\alpha)^2,$ for some
$\displaystyle (x-\alpha)^2,$ for some ![]() $\displaystyle \alpha \in F_{q}^{*},$ parameterized by the partitions
$\displaystyle \alpha \in F_{q}^{*},$ parameterized by the partitions ![]() $(1,1) $ and (2) of
$(1,1) $ and (2) of ![]() $2,$ respectively. We let
$2,$ respectively. We let ![]() $\displaystyle C^{(3)}$ denote the type of the conjugacy classes of elements having distinct eigen values in
$\displaystyle C^{(3)}$ denote the type of the conjugacy classes of elements having distinct eigen values in ![]() $F_q^{*}$. Further, note that for some
$F_q^{*}$. Further, note that for some  $\displaystyle y \in F_{q^2} \setminus
F_q,$ the matrix
$\displaystyle y \in F_{q^2} \setminus
F_q,$ the matrix  $$v = \begin{pmatrix} 0 & 1 \\ -y^{q+1} &
y+y^{q} \end{pmatrix}$$ is an element of
$$v = \begin{pmatrix} 0 & 1 \\ -y^{q+1} &
y+y^{q} \end{pmatrix}$$ is an element of ![]() $GL(2,q).$ We denote by
$GL(2,q).$ We denote by ![]() $C^{(4)}$ the types of conjugacy classes constituted by such irreducible elements of
$C^{(4)}$ the types of conjugacy classes constituted by such irreducible elements of ![]() $GL(2,q)$.
$GL(2,q)$.
Further, let ![]() $T^{(1)},$
$T^{(1)},$ ![]() $T^{(2)}$ and
$T^{(2)}$ and ![]() $T^{(3)}$ denote the types of conjugacy classes of the elements of
$T^{(3)}$ denote the types of conjugacy classes of the elements of ![]() $GL(3,q)$ with characteristic polynomial
$GL(3,q)$ with characteristic polynomial ![]() $\displaystyle (x-\alpha)^3,$ for some
$\displaystyle (x-\alpha)^3,$ for some ![]() $\displaystyle \alpha \in F_{q}^{*};$ parameterized by the partitions
$\displaystyle \alpha \in F_{q}^{*};$ parameterized by the partitions ![]() $(1,1,1), (2,1) $ and (3) of
$(1,1,1), (2,1) $ and (3) of ![]() $3,$ respectively. For any
$3,$ respectively. For any ![]() $\displaystyle \alpha \neq \beta \neq \gamma \neq \alpha \in F_q^{*},$ we denote by
$\displaystyle \alpha \neq \beta \neq \gamma \neq \alpha \in F_q^{*},$ we denote by ![]() $T^{(4)}$ and
$T^{(4)}$ and ![]() $T^{(5)}$ the types of conjugacy classes of the elements whose characteristic polynomial is
$T^{(5)}$ the types of conjugacy classes of the elements whose characteristic polynomial is ![]() $\displaystyle (x-\alpha)^2 (x - \beta),$ for the partitions
$\displaystyle (x-\alpha)^2 (x - \beta),$ for the partitions ![]() $(1,1)$ and (2) of
$(1,1)$ and (2) of ![]() $2,$ respectively. Further,
$2,$ respectively. Further, ![]() $T^{(6)}$ denotes the conjugacy class of elements of the form
$T^{(6)}$ denotes the conjugacy class of elements of the form ![]() $\displaystyle diag(\alpha, \beta, \gamma)$ and
$\displaystyle diag(\alpha, \beta, \gamma)$ and ![]() $\displaystyle T^{(7)}$ denotes the conjugacy class of the elements with characteristic polynomial
$\displaystyle T^{(7)}$ denotes the conjugacy class of the elements with characteristic polynomial ![]() $\displaystyle (x^2+ax+b)(x-\alpha),$ where
$\displaystyle (x^2+ax+b)(x-\alpha),$ where ![]() $\displaystyle (x^2+ax+b)$ is an irreducible polynomial over
$\displaystyle (x^2+ax+b)$ is an irreducible polynomial over ![]() $F_q.$ Finally,
$F_q.$ Finally, ![]() $\displaystyle T^{(8)}$ corresponds to the conjugacy class of irreducible elements.
$\displaystyle T^{(8)}$ corresponds to the conjugacy class of irreducible elements.
Now we determine the notation for the characters of ![]() $GL(2,q)$ and
$GL(2,q)$ and ![]() $GL(3,q)$. Let
$GL(3,q)$. Let ![]() $\displaystyle 0 \leq k, l \leq (q-2)$ be some integers. Then the linear character of
$\displaystyle 0 \leq k, l \leq (q-2)$ be some integers. Then the linear character of ![]() $GL(2,q)$ indexed by k is denoted as
$GL(2,q)$ indexed by k is denoted as  $\chi_k^{(1)}.$ The character of degree q obtained by tensoring the linear character
$\chi_k^{(1)}.$ The character of degree q obtained by tensoring the linear character  $\chi_k^{(1)}$ with the Steinberg character
$\chi_k^{(1)}$ with the Steinberg character ![]() $St^{(1,1)}$ is denoted by
$St^{(1,1)}$ is denoted by  $\displaystyle \chi_{k}^{(2)}.$ Further, for any
$\displaystyle \chi_{k}^{(2)}.$ Further, for any ![]() $\displaystyle k \neq l,$ the irreducible character parabolically induced from
$\displaystyle k \neq l,$ the irreducible character parabolically induced from ![]() $\chi_k \bigotimes \chi_l \in Irr(L_{(1,1)})$ is denoted by
$\chi_k \bigotimes \chi_l \in Irr(L_{(1,1)})$ is denoted by ![]() $\displaystyle \chi_{k,l}.$ Let T be the set of integers
$\displaystyle \chi_{k,l}.$ Let T be the set of integers ![]() $\displaystyle 1 \leq t \leq (q^2-1)$ such that
$\displaystyle 1 \leq t \leq (q^2-1)$ such that ![]() $(q+1) \nmid t$ and tq is excluded whenever t is included. Clearly,
$(q+1) \nmid t$ and tq is excluded whenever t is included. Clearly,  $\displaystyle |T| = \frac{q^2-q}{2}$. It is known that the number of cuspidal characters of
$\displaystyle |T| = \frac{q^2-q}{2}$. It is known that the number of cuspidal characters of ![]() $GL(2,q)$ is same as the size of
$GL(2,q)$ is same as the size of ![]() $T.$ A cuspidal character indexed by some
$T.$ A cuspidal character indexed by some ![]() $\displaystyle t \in T$ is denoted by
$\displaystyle t \in T$ is denoted by ![]() $\displaystyle \chi_{t}.$
$\displaystyle \chi_{t}.$
We denote the linear character of ![]() $GL(3,q)$ indexed by k as
$GL(3,q)$ indexed by k as  $\theta_k^{(1)}.$ The types of characters obtained by tensoring the Steinberg characters
$\theta_k^{(1)}.$ The types of characters obtained by tensoring the Steinberg characters ![]() $St^{(2,1)}$ and
$St^{(2,1)}$ and ![]() $St^{(1,1,1)}$ with the linear character
$St^{(1,1,1)}$ with the linear character  $\theta_k^{(1)}$ are denoted by
$\theta_k^{(1)}$ are denoted by  $\displaystyle \theta_k^{(2)}$ and
$\displaystyle \theta_k^{(2)}$ and  $\displaystyle \theta_k^{(3)},$ respectively. For any integer
$\displaystyle \theta_k^{(3)},$ respectively. For any integer ![]() $\displaystyle m \in \{0, 1, \ldots, (q-2)\},$ let
$\displaystyle m \in \{0, 1, \ldots, (q-2)\},$ let  $\displaystyle \theta_{k,l}^{(4)}, \theta_{k,l}^{(5)}$ and
$\displaystyle \theta_{k,l}^{(4)}, \theta_{k,l}^{(5)}$ and  $ \theta_{k,l,m}^{(6)}$ denote the characters
$ \theta_{k,l,m}^{(6)}$ denote the characters  $\displaystyle \chi_{k}^{(1)} \bigodot \chi_{l}, \ \chi_{k}^{(2)} \bigodot \chi_{l}$ and
$\displaystyle \chi_{k}^{(1)} \bigodot \chi_{l}, \ \chi_{k}^{(2)} \bigodot \chi_{l}$ and ![]() $ \chi_{k,m} \bigodot \chi_l (k \neq l \neq m \neq k)$, respectively. Further, for any
$ \chi_{k,m} \bigodot \chi_l (k \neq l \neq m \neq k)$, respectively. Further, for any ![]() $t \in T$ we let
$t \in T$ we let  $\theta_{t,l}^{(7)}$ denote the character
$\theta_{t,l}^{(7)}$ denote the character ![]() $\chi_{t} \bigodot \chi_l.$ Finally, we consider the set V of integers
$\chi_{t} \bigodot \chi_l.$ Finally, we consider the set V of integers ![]() $v \in \{0, 1, \ldots, q^3-1\}$ such that
$v \in \{0, 1, \ldots, q^3-1\}$ such that ![]() $ (q^2+q+1) \nmid v$ and vq, vq 2 are excluded whenever v is being chosen. Then the cuspidal characters of
$ (q^2+q+1) \nmid v$ and vq, vq 2 are excluded whenever v is being chosen. Then the cuspidal characters of ![]() $GL(3,q)$, indexed by
$GL(3,q)$, indexed by ![]() $v \in V,$ are denoted by
$v \in V,$ are denoted by ![]() $\theta_{v}^{(8)}$ and are
$\theta_{v}^{(8)}$ and are  $|V| = \frac{q^3-q}{3}$ many.
$|V| = \frac{q^3-q}{3}$ many.
We recall here that a cuspidal character of ![]() $GL(n,q)$ vanishes on all the non-primary conjugacy classes. For a proof of this fact, one can refer to [Reference Green7, pp. 64, 67 (Theorem 3.2 and Proposition 4.1)].
$GL(n,q)$ vanishes on all the non-primary conjugacy classes. For a proof of this fact, one can refer to [Reference Green7, pp. 64, 67 (Theorem 3.2 and Proposition 4.1)].
3. Quasi Steinberg cuspidal characters of  $GL(n,q)$
$GL(n,q)$
In this section, we classify the quasi r-Steinberg cuspidal characters of ![]() $\displaystyle GL(n,q).$ Observe that if
$\displaystyle GL(n,q).$ Observe that if ![]() $\displaystyle r=p,$ then for any
$\displaystyle r=p,$ then for any ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $q \geq 3,$ the matrix
$q \geq 3,$ the matrix ![]() $\displaystyle A = diag(\epsilon_1, 1, \ldots, 1)$ is an r-regular element of
$\displaystyle A = diag(\epsilon_1, 1, \ldots, 1)$ is an r-regular element of ![]() $\displaystyle GL(n,q).$ Since conjugacy class of A is not primary, a cuspidal character would vanish on it. Therefore, no cuspidal character is quasi p-Steinberg. Now assume that r is a prime different from
$\displaystyle GL(n,q).$ Since conjugacy class of A is not primary, a cuspidal character would vanish on it. Therefore, no cuspidal character is quasi p-Steinberg. Now assume that r is a prime different from ![]() $p.$
$p.$
We first obtain the quasi r-Steinberg cuspidal characters of ![]() $GL(2,q).$ When
$GL(2,q).$ When ![]() $q=2,$
$q=2,$ ![]() $\displaystyle |GL(2,2)| = 6$ and so r can be either 2 or 3. As
$\displaystyle |GL(2,2)| = 6$ and so r can be either 2 or 3. As ![]() $r \neq p, r=3.$ Since it follows from the character table that the cuspidal character of
$r \neq p, r=3.$ Since it follows from the character table that the cuspidal character of ![]() $GL(2,2)$ does not vanish on any conjugacy class, it implies that it is quasi 3-Steinberg. Thus we now characterize the quasi r-Steinberg cuspidal characters of
$GL(2,2)$ does not vanish on any conjugacy class, it implies that it is quasi 3-Steinberg. Thus we now characterize the quasi r-Steinberg cuspidal characters of ![]() $GL(2,q)$ when
$GL(2,q)$ when ![]() $\displaystyle q \geq 3:$
$\displaystyle q \geq 3:$
Proposition 3.1. Let r be a prime dividing the order of the group ![]() $GL(2,q),$ where
$GL(2,q),$ where ![]() $\displaystyle q \geq 3$ is a prime power. Then a cuspidal character of
$\displaystyle q \geq 3$ is a prime power. Then a cuspidal character of ![]() $GL(2,q)$ is quasi r-Steinberg if and only if
$GL(2,q)$ is quasi r-Steinberg if and only if ![]() $\displaystyle q=(r^{\beta}+1),$ for some
$\displaystyle q=(r^{\beta}+1),$ for some ![]() $\displaystyle \beta \in \mathbb{N}.$
$\displaystyle \beta \in \mathbb{N}.$
Proof. Let χt be a cuspidal character of ![]() $GL(2,q)$. Note that if
$GL(2,q)$. Note that if ![]() $\displaystyle r \ \nmid \ (q-1),$ then
$\displaystyle r \ \nmid \ (q-1),$ then ![]() $A = diag(\epsilon_1, 1)$ is an r-regular element. Since
$A = diag(\epsilon_1, 1)$ is an r-regular element. Since ![]() $\chi_t(A) = 0$, χt is not quasi r-Steinberg. Therefore, assume that
$\chi_t(A) = 0$, χt is not quasi r-Steinberg. Therefore, assume that ![]() $\displaystyle (q-1) = r^{\beta} \gamma,$ where
$\displaystyle (q-1) = r^{\beta} \gamma,$ where ![]() $\beta \geq 1$ and
$\beta \geq 1$ and ![]() $(r, \gamma) = 1.$ Now the following cases arise:
$(r, \gamma) = 1.$ Now the following cases arise:
Case I: ![]() $\displaystyle r \ | \ (q+1).$ As r also divides
$\displaystyle r \ | \ (q+1).$ As r also divides ![]() $(q-1)$, r = 2. If
$(q-1)$, r = 2. If ![]() $\displaystyle \gamma \gt 1,$ then
$\displaystyle \gamma \gt 1,$ then  $\displaystyle A_1 = diag(\epsilon_1^{\frac{q-1}{\gamma}}, 1)$ is 2-regular and its conjugacy class is not primary. Since
$\displaystyle A_1 = diag(\epsilon_1^{\frac{q-1}{\gamma}}, 1)$ is 2-regular and its conjugacy class is not primary. Since ![]() $\displaystyle \chi_t(A_1) = 0, \chi_t$ is not quasi 2-Steinberg.
$\displaystyle \chi_t(A_1) = 0, \chi_t$ is not quasi 2-Steinberg.
On the other hand, if ![]() $\displaystyle (q-1)=2^{\beta},$ then
$\displaystyle (q-1)=2^{\beta},$ then ![]() $\displaystyle (q+1) = 2^{\beta}+2.$ If
$\displaystyle (q+1) = 2^{\beta}+2.$ If ![]() $\displaystyle \beta=1,$ then
$\displaystyle \beta=1,$ then ![]() $\displaystyle
q=3.$ Note that the only 2-regular elements of
$\displaystyle
q=3.$ Note that the only 2-regular elements of ![]() $GL(2,3)$ are the identity matrix, say
$GL(2,3)$ are the identity matrix, say ![]() $I_2,$ and the matrix
$I_2,$ and the matrix  $$A_2=
\begin{pmatrix}
1 & 1 \\ 0 & 1
\end{pmatrix}$$. Since no cuspidal character vanishes on both of these elements, it follows that all the cuspidal characters of
$$A_2=
\begin{pmatrix}
1 & 1 \\ 0 & 1
\end{pmatrix}$$. Since no cuspidal character vanishes on both of these elements, it follows that all the cuspidal characters of ![]() $GL(2,3)$ are quasi 2-Steinberg. But if
$GL(2,3)$ are quasi 2-Steinberg. But if ![]() $\displaystyle \beta \gt 1,$ then
$\displaystyle \beta \gt 1,$ then ![]() $F_{q}^{*}$ is a 2-group and in this case the only 2-regular element of
$F_{q}^{*}$ is a 2-group and in this case the only 2-regular element of ![]() $GL(2,q)$ is A 2. The conjugacy class of A 2 is of type
$GL(2,q)$ is A 2. The conjugacy class of A 2 is of type ![]() $C^{(2)}$ and no cuspidal character vanishes on
$C^{(2)}$ and no cuspidal character vanishes on ![]() $C^{(2)}.$
$C^{(2)}.$
Now we examine whether χt vanishes on some irreducible 2-regular element of ![]() $GL(2,q)$ or not. Since
$GL(2,q)$ or not. Since ![]() $\displaystyle (q^2-1) = 2(q-1)(2^{\beta-1}+1),$ the 2-regular elements of
$\displaystyle (q^2-1) = 2(q-1)(2^{\beta-1}+1),$ the 2-regular elements of  $\displaystyle F_{q^2}^{*}$ are of the form
$\displaystyle F_{q^2}^{*}$ are of the form  $\displaystyle \epsilon_{2}^{2(q-1)l}$ for some divisor l of
$\displaystyle \epsilon_{2}^{2(q-1)l}$ for some divisor l of  $\displaystyle (2^{\beta-1}+1) = \frac{(q+1)}{2}.$ Thus an irreducible 2-regular element, say
$\displaystyle (2^{\beta-1}+1) = \frac{(q+1)}{2}.$ Thus an irreducible 2-regular element, say ![]() $A_3,$ of
$A_3,$ of ![]() $GL(2,q)$ is of form
$GL(2,q)$ is of form  $\displaystyle diag \Big(\epsilon_{2}^{2(q-1)l}, \epsilon_{2}^{2q(q-1)l} \Big)$. Note that
$\displaystyle diag \Big(\epsilon_{2}^{2(q-1)l}, \epsilon_{2}^{2q(q-1)l} \Big)$. Note that  $\displaystyle \chi_t(A_3) = \Big( \hat{\epsilon}_{2}^{2t(q-1)l} + \hat{\epsilon}_{2}^{2qt(q-1)l} \Big)
= 0$ if and only if
$\displaystyle \chi_t(A_3) = \Big( \hat{\epsilon}_{2}^{2t(q-1)l} + \hat{\epsilon}_{2}^{2qt(q-1)l} \Big)
= 0$ if and only if  $\displaystyle 2t(q-1)l = \frac{(q^2-1)}{2} - 2t(q-1)l.$ It further implies that
$\displaystyle 2t(q-1)l = \frac{(q^2-1)}{2} - 2t(q-1)l.$ It further implies that ![]() $\displaystyle 4tl = 2^{\beta-1}+1,$ which is not possible. Therefore, every cuspidal character is quasi 2-Steinberg.
$\displaystyle 4tl = 2^{\beta-1}+1,$ which is not possible. Therefore, every cuspidal character is quasi 2-Steinberg.
Case II: ![]() $\displaystyle r \ \nmid \ (q+1).$ First assume that
$\displaystyle r \ \nmid \ (q+1).$ First assume that ![]() $\displaystyle (q-1)$ has a prime divisor, say
$\displaystyle (q-1)$ has a prime divisor, say ![]() $\displaystyle r^{'},$ which is different from
$\displaystyle r^{'},$ which is different from ![]() $r.$ Then
$r.$ Then  $\displaystyle A_4 = diag(\epsilon_1^{\frac{q-1}{r^{'}}}, 1)$ is an r-regular element whose conjugacy class is not primary. It follows from the previous argument that no cuspidal character is quasi r-Steinberg in this case.
$\displaystyle A_4 = diag(\epsilon_1^{\frac{q-1}{r^{'}}}, 1)$ is an r-regular element whose conjugacy class is not primary. It follows from the previous argument that no cuspidal character is quasi r-Steinberg in this case.
Now assume that ![]() $\displaystyle (q-1) = r^{\beta},$ for some
$\displaystyle (q-1) = r^{\beta},$ for some ![]() $\displaystyle \beta \in \mathbb{N}.$ Since
$\displaystyle \beta \in \mathbb{N}.$ Since ![]() $\displaystyle r \ \nmid \ (q+1), r$ is some odd prime. As
$\displaystyle r \ \nmid \ (q+1), r$ is some odd prime. As ![]() $\displaystyle (q-1) = r^{\beta},$ no element in
$\displaystyle (q-1) = r^{\beta},$ no element in ![]() $C^{(1)}$ and
$C^{(1)}$ and ![]() $C^{(3)}$ is r-regular. Also, A 2 is the only r-regular element whose conjugacy class is of type
$C^{(3)}$ is r-regular. Also, A 2 is the only r-regular element whose conjugacy class is of type ![]() $C^{(2)}.$ One can check that no cuspidal character vanishes on it. Further, since
$C^{(2)}.$ One can check that no cuspidal character vanishes on it. Further, since ![]() $\displaystyle (q^2-1)=r^{\beta}(r^{\beta}+2),$ the only irreducible r-regular element of
$\displaystyle (q^2-1)=r^{\beta}(r^{\beta}+2),$ the only irreducible r-regular element of ![]() $GL(2,q)$ is of form
$GL(2,q)$ is of form  $A_5 = diag \Big(\epsilon_{2}^{r^{\beta}l}, \epsilon_{2}^{qr^{\beta}l} \Big),$ where l is some divisor of
$A_5 = diag \Big(\epsilon_{2}^{r^{\beta}l}, \epsilon_{2}^{qr^{\beta}l} \Big),$ where l is some divisor of ![]() $(r^{\beta}+2)$. Note that
$(r^{\beta}+2)$. Note that ![]() $\displaystyle \chi_t(A_5) = 0$ if and only if
$\displaystyle \chi_t(A_5) = 0$ if and only if  $\displaystyle \frac{(r^{\beta}+2)}{tl} = 4,$ which is not possible since r is odd. Therefore, even in this case every cuspidal character of is quasi r-Steinberg.
$\displaystyle \frac{(r^{\beta}+2)}{tl} = 4,$ which is not possible since r is odd. Therefore, even in this case every cuspidal character of is quasi r-Steinberg.
Note that it follows from Theorem 49.8 in [Reference Bump2] that the degree of a cuspidal character of ![]() $GL(n,q)$ is
$GL(n,q)$ is  $\displaystyle \prod_{i=1}^{n-1} (q^i-1)$. Thus the degree of a cuspidal character of
$\displaystyle \prod_{i=1}^{n-1} (q^i-1)$. Thus the degree of a cuspidal character of ![]() $GL(2,q)$ is
$GL(2,q)$ is ![]() $(q-1)$. Now the above discussion leads to the following:
$(q-1)$. Now the above discussion leads to the following:
Remark 3.2. If a cuspidal character of ![]() $GL(2,q)$ is quasi r-Steinberg, then its degree is an r-power.
$GL(2,q)$ is quasi r-Steinberg, then its degree is an r-power.
In the following, we classify the quasi r-Steinberg cuspidal characters of ![]() $GL(n,q):$
$GL(n,q):$
Proof of Theorem 1.2
Letϕ be a cuspidal character of ![]() $GL(n,q)$. Assume that
$GL(n,q)$. Assume that ![]() $\displaystyle q \geq 3.$ If
$\displaystyle q \geq 3.$ If ![]() $\displaystyle r \ \nmid \ (q-1),$ then
$\displaystyle r \ \nmid \ (q-1),$ then ![]() $A = diag(\epsilon_1, 1, \ldots, 1)$ is an r-regular element of
$A = diag(\epsilon_1, 1, \ldots, 1)$ is an r-regular element of ![]() $GL(n,q)$. Since ϕ vanishes on A, it is not quasi r-Steinberg. On the other hand, when
$GL(n,q)$. Since ϕ vanishes on A, it is not quasi r-Steinberg. On the other hand, when ![]() $\displaystyle r \ \mid \ (q-1),$ the following cases arise:
$\displaystyle r \ \mid \ (q-1),$ the following cases arise:
Case I: ![]() $\displaystyle r \ \nmid \ (q+1).$ If
$\displaystyle r \ \nmid \ (q+1).$ If ![]() $\displaystyle n \geq 3,$ then
$\displaystyle n \geq 3,$ then  $\displaystyle B_1 = diag(\epsilon_2^{q-1}, \epsilon_2^{q(q-1)}, 1, \ldots, 1)$ is an r-regular element of
$\displaystyle B_1 = diag(\epsilon_2^{q-1}, \epsilon_2^{q(q-1)}, 1, \ldots, 1)$ is an r-regular element of ![]() $GL(n,q).$ Since the conjugacy class
$GL(n,q).$ Since the conjugacy class ![]() $[B_1]$ is not primary, it follows that ϕ is not quasi r-Steinberg.
$[B_1]$ is not primary, it follows that ϕ is not quasi r-Steinberg.
Case II: ![]() $\displaystyle r \ | \ (q+1).$ Since
$\displaystyle r \ | \ (q+1).$ Since ![]() $\displaystyle r \ \mid \ (q-1),$ r = 2. Assume that
$\displaystyle r \ \mid \ (q-1),$ r = 2. Assume that ![]() $\displaystyle (q-1) = 2^{\beta} \gamma,$ where
$\displaystyle (q-1) = 2^{\beta} \gamma,$ where ![]() $\displaystyle \beta \geq 1$ and
$\displaystyle \beta \geq 1$ and ![]() $(\gamma,2)=1.$ If
$(\gamma,2)=1.$ If ![]() $\displaystyle \gamma \gt 1,$ then
$\displaystyle \gamma \gt 1,$ then  $\displaystyle B_2 = diag \Big(\epsilon_1^{\frac{q-1}{\gamma}}, 1, \ldots, 1 \Big)$ is 2-regular and its conjugacy class is not primary. Therefore, the previous argument implies that ϕ is not quasi 2-Steinberg.
$\displaystyle B_2 = diag \Big(\epsilon_1^{\frac{q-1}{\gamma}}, 1, \ldots, 1 \Big)$ is 2-regular and its conjugacy class is not primary. Therefore, the previous argument implies that ϕ is not quasi 2-Steinberg.
But if ![]() $\displaystyle \gamma = 1,$ then
$\displaystyle \gamma = 1,$ then ![]() $\displaystyle (q-1) = 2^{\beta}.$ If
$\displaystyle (q-1) = 2^{\beta}.$ If ![]() $\displaystyle \beta=1,$ then
$\displaystyle \beta=1,$ then ![]() $\displaystyle q=3.$ Now for any
$\displaystyle q=3.$ Now for any ![]() $\displaystyle n \gt 3,$
$\displaystyle n \gt 3,$ ![]() $\displaystyle (3^n-3^{n-3}) = 3^{n-3}(13)(2)$ is a divisor of
$\displaystyle (3^n-3^{n-3}) = 3^{n-3}(13)(2)$ is a divisor of ![]() $\displaystyle |GL(n,3)|.$ Now as
$\displaystyle |GL(n,3)|.$ Now as  $$\displaystyle B_3 =
\begin{pmatrix}
0 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 2 & 1 \end{pmatrix}$$ is of order
$$\displaystyle B_3 =
\begin{pmatrix}
0 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 2 & 1 \end{pmatrix}$$ is of order ![]() $13,$ the element
$13,$ the element ![]() $\displaystyle B_4 = diag(B_3, 1, \ldots, 1) \in GL(n,3)$ is 2-regular. Therefore, for any
$\displaystyle B_4 = diag(B_3, 1, \ldots, 1) \in GL(n,3)$ is 2-regular. Therefore, for any ![]() $n \gt 3,$ no cuspidal character of
$n \gt 3,$ no cuspidal character of ![]() $GL(n,3)$ is quasi 2-Steinberg. When
$GL(n,3)$ is quasi 2-Steinberg. When ![]() $n=3,$ the only 2-regular elements of
$n=3,$ the only 2-regular elements of ![]() $GL(3,3)$ are the elements of order 13. Now note that the degree of any cuspidal character of
$GL(3,3)$ are the elements of order 13. Now note that the degree of any cuspidal character of ![]() $GL(3,3)$ is
$GL(3,3)$ is ![]() $(3-1)(3^2-1)=16$ and it follows from the character table of
$(3-1)(3^2-1)=16$ and it follows from the character table of ![]() $GL(3,3)$ that no character of degree 16 vanishes on any element of order 13. Therefore, every cuspidal character of
$GL(3,3)$ that no character of degree 16 vanishes on any element of order 13. Therefore, every cuspidal character of ![]() $GL(3,3)$ is quasi 2-Steinberg.
$GL(3,3)$ is quasi 2-Steinberg.
Further, if ![]() $\displaystyle \beta \gt 1,$ then
$\displaystyle \beta \gt 1,$ then ![]() $\displaystyle (q+1) = 2(2^{\beta-1}+1).$ Observe that for any
$\displaystyle (q+1) = 2(2^{\beta-1}+1).$ Observe that for any ![]() $\displaystyle n \geq 3,$ the conjugacy class of the 2-regular element
$\displaystyle n \geq 3,$ the conjugacy class of the 2-regular element  $\displaystyle diag(\epsilon_2^{2(q-1)}, \epsilon_2^{2q(q-1)}, 1, \ldots, 1)$ is not primary. Therefore, even in this case no cuspidal character is quasi r-Steinberg.
$\displaystyle diag(\epsilon_2^{2(q-1)}, \epsilon_2^{2q(q-1)}, 1, \ldots, 1)$ is not primary. Therefore, even in this case no cuspidal character is quasi r-Steinberg.
Now consider the group ![]() $GL(n,2),$ where
$GL(n,2),$ where ![]() $n \geq 3.$ Note that if
$n \geq 3.$ Note that if ![]() $r \neq 3,$ then
$r \neq 3,$ then ![]() $(q+1) = 3.$ Therefore, the argument in Case I provides that no cuspidal character of
$(q+1) = 3.$ Therefore, the argument in Case I provides that no cuspidal character of ![]() $GL(n,2)$ is quasi r-Steinberg. If
$GL(n,2)$ is quasi r-Steinberg. If ![]() $r=3,$ then for any
$r=3,$ then for any ![]() $\displaystyle n \geq 4, B_4 = diag(E_3, 1, \ldots, 1)$ is a 3-regular element of
$\displaystyle n \geq 4, B_4 = diag(E_3, 1, \ldots, 1)$ is a 3-regular element of ![]() $GL(n,2)$. As
$GL(n,2)$. As ![]() $\phi(B_4) = 0, \phi$ is not quasi 3-Steinberg. Further, it follows from the character table that every cuspidal character
$\phi(B_4) = 0, \phi$ is not quasi 3-Steinberg. Further, it follows from the character table that every cuspidal character ![]() $GL(3,2)$ is quasi 3-Steinberg. Now the result follows from Proposition 3.1.
$GL(3,2)$ is quasi 3-Steinberg. Now the result follows from Proposition 3.1.
4. Quasi Steinberg characters of  $GL(2,q)$
$GL(2,q)$
In this section, we obtain a characterization of the nonlinear quasi r-Steinberg characters of ![]() $\displaystyle GL(2,q).$ In this direction, we start with the parabolically induced characters of
$\displaystyle GL(2,q).$ In this direction, we start with the parabolically induced characters of ![]() $GL(2,q)$. We first make the following remark towards this end:
$GL(2,q)$. We first make the following remark towards this end:
Remark 4.1. Let n be an odd prime and ![]() $\displaystyle r$ be a prime divisor of
$\displaystyle r$ be a prime divisor of ![]() $|GL(n,q)|$ different from p. Assume that
$|GL(n,q)|$ different from p. Assume that ![]() $\displaystyle r \ | \ (q^i-1),$ for some
$\displaystyle r \ | \ (q^i-1),$ for some ![]() $\displaystyle 1 \lt i \lt n.$ If r is also a divisor of
$\displaystyle 1 \lt i \lt n.$ If r is also a divisor of ![]() $(q^n-1),$ then since
$(q^n-1),$ then since ![]() $\displaystyle gcd(q^i-1, q^n-1) = (q^{gcd(i,n)}-1) = (q-1),$
$\displaystyle gcd(q^i-1, q^n-1) = (q^{gcd(i,n)}-1) = (q-1),$ ![]() $\displaystyle r \ | \ (q-1).$ It further implies that
$\displaystyle r \ | \ (q-1).$ It further implies that  $\displaystyle r \ \nmid \ \frac{(q^i-1)}{q-1}.$ Indeed if r divides
$\displaystyle r \ \nmid \ \frac{(q^i-1)}{q-1}.$ Indeed if r divides  $\displaystyle \frac{(q^i-1)}{q-1},$ then since
$\displaystyle \frac{(q^i-1)}{q-1},$ then since  $\displaystyle gcd \Big(\frac{q^i-1}{q-1}, q^n-1 \Big) = 1,$
$\displaystyle gcd \Big(\frac{q^i-1}{q-1}, q^n-1 \Big) = 1,$ ![]() $\displaystyle r \ | \ 1,$ which is not possible.
$\displaystyle r \ | \ 1,$ which is not possible.
In the following, we establish a necessary condition for a parabolically induced character to be quasi r-Steinberg:
Lemma 4.2. Let n be a prime and ![]() $\displaystyle r (\neq p)$ be a prime divisor of
$\displaystyle r (\neq p)$ be a prime divisor of ![]() $|GL(n,q)|.$ If a parabolically induced character ψ of
$|GL(n,q)|.$ If a parabolically induced character ψ of ![]() $GL(n,q)$ is quasi r-Steinberg, then r is the only prime divisor of
$GL(n,q)$ is quasi r-Steinberg, then r is the only prime divisor of  $\displaystyle \frac{(q^n-1)}{(q-1)}$.
$\displaystyle \frac{(q^n-1)}{(q-1)}$.
Proof. Assume that n is an odd prime. If r is ![]() $2,$ then since
$2,$ then since  $\displaystyle \frac{(q^n-1)}{(q-1)} = \sum_{j=0}^{n-1} q^j$ is odd,
$\displaystyle \frac{(q^n-1)}{(q-1)} = \sum_{j=0}^{n-1} q^j$ is odd,  $\displaystyle r \nmid \frac{(q^n-1)}{(q-1)}.$ Thus
$\displaystyle r \nmid \frac{(q^n-1)}{(q-1)}.$ Thus  $\displaystyle B = diag(\epsilon_n^{q-1}, \epsilon_n^{q(q-1)}, \ldots, \epsilon_n^{q^{n-1}(q-1)})$ is an r-regular element of
$\displaystyle B = diag(\epsilon_n^{q-1}, \epsilon_n^{q(q-1)}, \ldots, \epsilon_n^{q^{n-1}(q-1)})$ is an r-regular element of ![]() $GL(n,q).$ Note that the order
$GL(n,q).$ Note that the order  $\displaystyle \sum_{j=0}^{n-1} q^j$ of
$\displaystyle \sum_{j=0}^{n-1} q^j$ of ![]() $\epsilon_n^{q-1}$ does not divide
$\epsilon_n^{q-1}$ does not divide ![]() $\displaystyle (q^i-1),$ for any
$\displaystyle (q^i-1),$ for any ![]() $\displaystyle 1 \leq i \lt n.$ Therefore,
$\displaystyle 1 \leq i \lt n.$ Therefore,  $\epsilon_n^{q-1} \in F_{q^{n}}^{*} \setminus F_{q^{i}}^{*} \ \forall \ 1 \leq i \lt n$ and so B is an irreducible element of
$\epsilon_n^{q-1} \in F_{q^{n}}^{*} \setminus F_{q^{i}}^{*} \ \forall \ 1 \leq i \lt n$ and so B is an irreducible element of ![]() $GL(n,q)$. Since the conjugacy class of an irreducible element of
$GL(n,q)$. Since the conjugacy class of an irreducible element of ![]() $GL(n,q)$ intersects
$GL(n,q)$ intersects ![]() $\displaystyle P_{\lambda}$ trivially,
$\displaystyle P_{\lambda}$ trivially, ![]() $\displaystyle \psi(B) = 0.$ Therefore, ψ is not quasi r-Steinberg.
$\displaystyle \psi(B) = 0.$ Therefore, ψ is not quasi r-Steinberg.
Now consider the case when r is an odd prime. Note that if ![]() $\displaystyle r \ | \ (q+1),$ then
$\displaystyle r \ | \ (q+1),$ then  $\displaystyle r \ \nmid \sum_{j=0}^{n-1} q^j$. Thus the previous argument implies that ψ is not quasi r-Steinberg. Now let
$\displaystyle r \ \nmid \sum_{j=0}^{n-1} q^j$. Thus the previous argument implies that ψ is not quasi r-Steinberg. Now let ![]() $\displaystyle r \ \nmid (q+1).$ Suppose
$\displaystyle r \ \nmid (q+1).$ Suppose  $\displaystyle \sum_{j=0}^{n-1} q^j = r^{\delta}k,$ where
$\displaystyle \sum_{j=0}^{n-1} q^j = r^{\delta}k,$ where ![]() $(r,k)=1$ and
$(r,k)=1$ and ![]() $\delta \geq 0$ is an integer. If
$\delta \geq 0$ is an integer. If ![]() $k=1,$ then
$k=1,$ then  $\displaystyle \frac{(q^n-1)}{(q-1)}$ is an r-power and our claim is established. On the other hand, if
$\displaystyle \frac{(q^n-1)}{(q-1)}$ is an r-power and our claim is established. On the other hand, if ![]() $k \gt 1,$ then the order of
$k \gt 1,$ then the order of  $\displaystyle \epsilon = \epsilon_n^{(q-1)r^{\delta}}$ is k and so
$\displaystyle \epsilon = \epsilon_n^{(q-1)r^{\delta}}$ is k and so  $\displaystyle B^{'} = diag(\epsilon, \epsilon^q, \ldots, \epsilon^{q^{n-1}})$ is an r-regular element of
$\displaystyle B^{'} = diag(\epsilon, \epsilon^q, \ldots, \epsilon^{q^{n-1}})$ is an r-regular element of ![]() $GL(n,q)$. Further, note that
$GL(n,q)$. Further, note that ![]() $B^{'}$ is irreducible if and only if
$B^{'}$ is irreducible if and only if ![]() $\displaystyle o(\epsilon) = k \ \nmid \ (q^i-1),$ for any
$\displaystyle o(\epsilon) = k \ \nmid \ (q^i-1),$ for any ![]() $1 \leq i \leq (n-1).$ Since
$1 \leq i \leq (n-1).$ Since  $\displaystyle \Big(q^i-1, \frac{(q^n-1)}{(q-1)} \Big) = 1,$ it follows that
$\displaystyle \Big(q^i-1, \frac{(q^n-1)}{(q-1)} \Big) = 1,$ it follows that  $\displaystyle \frac{(q^i-1)}{k}$ is not an integer. Thus
$\displaystyle \frac{(q^i-1)}{k}$ is not an integer. Thus ![]() $B^{'}$ is an irreducible r-regular element and ψ vanishes on it. It implies that no parabolically induced character of
$B^{'}$ is an irreducible r-regular element and ψ vanishes on it. It implies that no parabolically induced character of ![]() $GL(n,q)$ is quasi r-Steinberg in this case.
$GL(n,q)$ is quasi r-Steinberg in this case.
Finally, we consider the case of ![]() $\displaystyle n=2.$ If
$\displaystyle n=2.$ If ![]() $\displaystyle r \ \nmid \ (q+1),$ then the element
$\displaystyle r \ \nmid \ (q+1),$ then the element  $\displaystyle diag(\epsilon_2^{(q-1)}, \epsilon_2^{q(q-1)})$ is an irreducible r-regular element of
$\displaystyle diag(\epsilon_2^{(q-1)}, \epsilon_2^{q(q-1)})$ is an irreducible r-regular element of ![]() $GL(2,q)$ and the previous argument again implies that no parabolically induced character is quasi r-Steinberg. Further, assume that
$GL(2,q)$ and the previous argument again implies that no parabolically induced character is quasi r-Steinberg. Further, assume that ![]() $\displaystyle (q+1) = r^{\beta} \gamma,$ where
$\displaystyle (q+1) = r^{\beta} \gamma,$ where ![]() $\displaystyle \beta \geq 1$ and
$\displaystyle \beta \geq 1$ and ![]() $\displaystyle (r, \gamma) = 1.$ If
$\displaystyle (r, \gamma) = 1.$ If ![]() $\displaystyle \gamma \gt 1,$ then in the following we prove that there always exists an r-regular element on which ψ vanishes:
$\displaystyle \gamma \gt 1,$ then in the following we prove that there always exists an r-regular element on which ψ vanishes:
•
 $r \nmid (q-1)$: If
$r \nmid (q-1)$: If  $\gamma \ | \ (q-1),$ then
$\gamma \ | \ (q-1),$ then  $\displaystyle \gamma = 2.$ Let
$\displaystyle \gamma = 2.$ Let  $\displaystyle (q-1) = 2^{\alpha} \kappa,$ where
$\displaystyle (q-1) = 2^{\alpha} \kappa,$ where  $\displaystyle (2, \kappa) = 1.$ Then
$\displaystyle (2, \kappa) = 1.$ Then  $\displaystyle diag(\epsilon_2^{\frac{(q^2-1)}{2^{\alpha+1}}}, \epsilon_2^{\frac{q(q^2-1)}{2^{\alpha+1}}})$ is an irreducible r-regular element. If
$\displaystyle diag(\epsilon_2^{\frac{(q^2-1)}{2^{\alpha+1}}}, \epsilon_2^{\frac{q(q^2-1)}{2^{\alpha+1}}})$ is an irreducible r-regular element. If  $\displaystyle \gamma \nmid \ (q-1),$ then
$\displaystyle \gamma \nmid \ (q-1),$ then  $\displaystyle diag(\epsilon_2^{\frac{(q^2-1)}{\gamma}}, \epsilon_2^{\frac{q(q^2-1)}{\gamma}})$ is an irreducible r-regular element.
$\displaystyle diag(\epsilon_2^{\frac{(q^2-1)}{\gamma}}, \epsilon_2^{\frac{q(q^2-1)}{\gamma}})$ is an irreducible r-regular element.•
 $r \mid (q-1)$: If
$r \mid (q-1)$: If  $\displaystyle \gamma \ | \ (q-1),$ then
$\displaystyle \gamma \ | \ (q-1),$ then  $\displaystyle \gamma = 2,$ which is not possible as r = 2. Therefore,
$\displaystyle \gamma = 2,$ which is not possible as r = 2. Therefore,  $\displaystyle \gamma \nmid \ (q-1);$ and hence
$\displaystyle \gamma \nmid \ (q-1);$ and hence  $\displaystyle s_3$ is an irreducible r-regular element.
$\displaystyle s_3$ is an irreducible r-regular element.
Therefore, ψ is not quasi r-Steinberg. Further, for ![]() $\gamma = 1,$
$\gamma = 1,$ ![]() $\displaystyle (q+1) = r^{\beta}$. Now the result follows.
$\displaystyle (q+1) = r^{\beta}$. Now the result follows.
We now classify the quasi r-Steinberg characters of ![]() $GL(2,q)$:
$GL(2,q)$:
Theorem 4.3. Let ![]() $q \geq 3$ be a prime power, r be a prime dividing
$q \geq 3$ be a prime power, r be a prime dividing ![]() $\displaystyle |GL(2,q)|$ and
$\displaystyle |GL(2,q)|$ and  $\displaystyle \chi \in \Big\{\chi_k^{(2)}, \chi_{k,l} \ | \ 0 \leq k \lt l \leq (q-2) \Big\}.$
$\displaystyle \chi \in \Big\{\chi_k^{(2)}, \chi_{k,l} \ | \ 0 \leq k \lt l \leq (q-2) \Big\}.$
1. If
 $\displaystyle r=p,$ then χ is quasi p-Steinberg if and only if
$\displaystyle r=p,$ then χ is quasi p-Steinberg if and only if  $\displaystyle \chi$ is of type
$\displaystyle \chi$ is of type  $\chi_k^{(2)}.$
$\chi_k^{(2)}.$2. If
 $\displaystyle r \neq p,$ then χ is quasi r-Steinberg if and only if
$\displaystyle r \neq p,$ then χ is quasi r-Steinberg if and only if  $\displaystyle \chi$ is of type
$\displaystyle \chi$ is of type  $\chi_{k,l}$ and
$\chi_{k,l}$ and  $\displaystyle q = (r^{\delta}-1).$
$\displaystyle q = (r^{\delta}-1).$
Proof. First assume that ![]() $\displaystyle r = p.$ Note that any character of degree q vanishes only on the elements of the form
$\displaystyle r = p.$ Note that any character of degree q vanishes only on the elements of the form  $$ t_{\alpha} =
\begin{pmatrix}
\alpha & 1 \\ 0 & \alpha
\end{pmatrix} \in C^{(2)},$$ for some
$$ t_{\alpha} =
\begin{pmatrix}
\alpha & 1 \\ 0 & \alpha
\end{pmatrix} \in C^{(2)},$$ for some ![]() $\displaystyle \alpha \in F_{q}^{*}.$ Since
$\displaystyle \alpha \in F_{q}^{*}.$ Since ![]() $\displaystyle o(t_{\alpha}) = lcm(o(\alpha), p),$ no element of
$\displaystyle o(t_{\alpha}) = lcm(o(\alpha), p),$ no element of ![]() $C^{(2)}$ is p-regular. Therefore, for any
$C^{(2)}$ is p-regular. Therefore, for any ![]() $\displaystyle 0 \leq k \leq (q-2),$
$\displaystyle 0 \leq k \leq (q-2),$  $\displaystyle \chi_k^{(2)}$ is a quasi p-Steinberg character. Also, a parabolically induced character vanishes on the irreducible r-regular element E 2 and hence is not quasi p-Steinberg.
$\displaystyle \chi_k^{(2)}$ is a quasi p-Steinberg character. Also, a parabolically induced character vanishes on the irreducible r-regular element E 2 and hence is not quasi p-Steinberg.
Further, let ![]() $\displaystyle r \neq p.$ In this case, t 1 is an r-regular element of
$\displaystyle r \neq p.$ In this case, t 1 is an r-regular element of ![]() $GL(2,q).$ Since
$GL(2,q).$ Since  $\displaystyle \chi_k^{(2)}$ vanishes on t 1, it is not quasi r-Steinberg. Now we study when a parabolically induced character of
$\displaystyle \chi_k^{(2)}$ vanishes on t 1, it is not quasi r-Steinberg. Now we study when a parabolically induced character of ![]() $GL(2,q)$ is quasi r-Steinberg. In this direction, a necessary condition provided by Lemma 4.2 is that
$GL(2,q)$ is quasi r-Steinberg. In this direction, a necessary condition provided by Lemma 4.2 is that ![]() $\displaystyle (q+1) = r^{\beta},$ for some
$\displaystyle (q+1) = r^{\beta},$ for some ![]() $\beta \in \mathbb{N}.$
$\beta \in \mathbb{N}.$
Let ![]() $\chi_{k,l}$ be a parabolically induced character, where
$\chi_{k,l}$ be a parabolically induced character, where ![]() $0 \leq k \lt l \leq (q-2)$. It follows from the character table that it takes 0 value only on the elements whose conjugacy class is of type
$0 \leq k \lt l \leq (q-2)$. It follows from the character table that it takes 0 value only on the elements whose conjugacy class is of type ![]() $\displaystyle C^{(3)}$ or
$\displaystyle C^{(3)}$ or ![]() $\displaystyle C^{(4)}.$ Observe that if r is some odd prime, then
$\displaystyle C^{(4)}.$ Observe that if r is some odd prime, then ![]() $r \ \nmid \ (q-1)$. Indeed, if
$r \ \nmid \ (q-1)$. Indeed, if ![]() $r \ | \ (q-1),$ then
$r \ | \ (q-1),$ then ![]() $r=2,$ which is not the case. Now since
$r=2,$ which is not the case. Now since ![]() $\displaystyle (q^2-1)=(q-1)r^{\beta},$ it follows that no irreducible element of
$\displaystyle (q^2-1)=(q-1)r^{\beta},$ it follows that no irreducible element of ![]() $GL(2,q)$ is r-regular. Therefore, the elements whose conjugacy class is of type
$GL(2,q)$ is r-regular. Therefore, the elements whose conjugacy class is of type ![]() $\displaystyle C^{(4)}$ are not r-regular.
$\displaystyle C^{(4)}$ are not r-regular.
Further, let ![]() $\displaystyle V = diag(\alpha, \beta)$ has conjugacy class of type
$\displaystyle V = diag(\alpha, \beta)$ has conjugacy class of type ![]() $C^{(3)}.$ Then
$C^{(3)}.$ Then  $\chi_{k,l}(V) = \hat{\alpha}^k \hat{\beta}^l + \hat{\alpha}^l \hat{\beta}^k = 0$ if and only if
$\chi_{k,l}(V) = \hat{\alpha}^k \hat{\beta}^l + \hat{\alpha}^l \hat{\beta}^k = 0$ if and only if ![]() $F_{q}^{*}$ contains the primitive second root of unity. Since r being odd implies q is even, this is also not the case. Therefore,
$F_{q}^{*}$ contains the primitive second root of unity. Since r being odd implies q is even, this is also not the case. Therefore, ![]() $\displaystyle \chi_{k,l}$ is quasi r-Steinberg.
$\displaystyle \chi_{k,l}$ is quasi r-Steinberg.
Now if ![]() $\displaystyle (q+1) = 2^{\delta},$ then
$\displaystyle (q+1) = 2^{\delta},$ then ![]() $\displaystyle (q-1) = 2(2^{\delta-1}-1).$ Note that
$\displaystyle (q-1) = 2(2^{\delta-1}-1).$ Note that ![]() $\displaystyle \delta = 2$ implies q = 3. Since there is no 2-regular element in
$\displaystyle \delta = 2$ implies q = 3. Since there is no 2-regular element in ![]() $C^{(3)}$ and
$C^{(3)}$ and ![]() $C^{(4)}$, the parabolically induced characters of
$C^{(4)}$, the parabolically induced characters of ![]() $GL(2,3)$ are quasi 2-Steinberg. Further, if
$GL(2,3)$ are quasi 2-Steinberg. Further, if ![]() $\displaystyle \delta \geq 3,$ then there is no 2-regular element in
$\displaystyle \delta \geq 3,$ then there is no 2-regular element in ![]() $C^{(4)}.$ On the other hand, assume that the conjugacy class of
$C^{(4)}.$ On the other hand, assume that the conjugacy class of ![]() $\displaystyle W = diag(\epsilon_1^{s_1}, \epsilon_1^{s_2}),$ for some
$\displaystyle W = diag(\epsilon_1^{s_1}, \epsilon_1^{s_2}),$ for some ![]() $\displaystyle 0 \leq s_1 \lt s_2 \leq (q-2),$ is of type
$\displaystyle 0 \leq s_1 \lt s_2 \leq (q-2),$ is of type ![]() $C^{(3)}.$ Then
$C^{(3)}.$ Then  $\displaystyle \chi_{k,l}(W) = \hat{\epsilon_1}^{s_1k+s_2l} + \hat{\epsilon_1}^{s_1l+s_2k}
= 0$ if and only if
$\displaystyle \chi_{k,l}(W) = \hat{\epsilon_1}^{s_1k+s_2l} + \hat{\epsilon_1}^{s_1l+s_2k}
= 0$ if and only if  $\displaystyle (s_2-s_1)(l-k) = \frac{(q-1)}{2}.$ Observe that a pair of such distinct elements s 1 and s 2 exists if
$\displaystyle (s_2-s_1)(l-k) = \frac{(q-1)}{2}.$ Observe that a pair of such distinct elements s 1 and s 2 exists if ![]() $\displaystyle (l-k)$ is invertible in
$\displaystyle (l-k)$ is invertible in ![]() $\displaystyle \mathbb{Z}_{q-1}$. Further, note that for any
$\displaystyle \mathbb{Z}_{q-1}$. Further, note that for any  $\displaystyle 1 \leq i \leq 2, \ o(\epsilon_i^{s_i}) = \frac{(q-1)}{s_i}$ and so
$\displaystyle 1 \leq i \leq 2, \ o(\epsilon_i^{s_i}) = \frac{(q-1)}{s_i}$ and so  $\displaystyle o(W) = lcm \Big( \frac{(q-1)}{s_1}, \frac{(q-1)}{s_2} \Big).$ Since s 1 and s 2 have different parity, 2 divides
$\displaystyle o(W) = lcm \Big( \frac{(q-1)}{s_1}, \frac{(q-1)}{s_2} \Big).$ Since s 1 and s 2 have different parity, 2 divides ![]() $o(W).$ Therefore, W is not a 2-regular element. Thus an element of
$o(W).$ Therefore, W is not a 2-regular element. Thus an element of ![]() $C^{(3)}$ on which
$C^{(3)}$ on which ![]() $\chi_{k,l}$ vanishes, is not 2-regular. It implies that if
$\chi_{k,l}$ vanishes, is not 2-regular. It implies that if ![]() $\displaystyle (l-k)$ is invertible in
$\displaystyle (l-k)$ is invertible in ![]() $\displaystyle \mathbb{Z}_{q-1},$ then
$\displaystyle \mathbb{Z}_{q-1},$ then ![]() $\chi_{k,l}$ is quasi 2-Steinberg. On the other hand, if
$\chi_{k,l}$ is quasi 2-Steinberg. On the other hand, if ![]() $\displaystyle (l-k)$ is not invertible in
$\displaystyle (l-k)$ is not invertible in ![]() $\displaystyle \mathbb{Z}_{q-1},$ then there does not exist any element in
$\displaystyle \mathbb{Z}_{q-1},$ then there does not exist any element in ![]() $\displaystyle C^{(3)}$ on which
$\displaystyle C^{(3)}$ on which ![]() $\displaystyle \chi_{k,l}$ vanishes. Now the result follows.
$\displaystyle \chi_{k,l}$ vanishes. Now the result follows.
5. Quasi Steinberg characters of  $GL(3,q)$
$GL(3,q)$
In this section, we classify the quasi r-Steinberg characters of ![]() $GL(3,q).$ Since the discussion on the cuspidal characters has been done in § 3, we now continue the study for the remaining nonlinear characters of
$GL(3,q).$ Since the discussion on the cuspidal characters has been done in § 3, we now continue the study for the remaining nonlinear characters of ![]() $GL(3,q)$:
$GL(3,q)$:
Theorem 5.1. Let us denote by S the set constituted by all the irreducible characters of ![]() $GL(3,q)$ except the linear and cuspidal ones. If
$GL(3,q)$ except the linear and cuspidal ones. If ![]() $r = p,$ then the only characters in S that are quasi p-Steinberg are of type
$r = p,$ then the only characters in S that are quasi p-Steinberg are of type  $\displaystyle \theta_k^{(3)}$. If
$\displaystyle \theta_k^{(3)}$. If ![]() $r \neq p,$ then we have the following:
$r \neq p,$ then we have the following:
1. If q is even, then the characters of type
 $\displaystyle \theta_{k,l}^{(4)}$ are quasi r-Steinberg if and only if
$\displaystyle \theta_{k,l}^{(4)}$ are quasi r-Steinberg if and only if  $(1+q+q^2)$ is an r-power.
$(1+q+q^2)$ is an r-power.2. If q is odd, then the characters of type
 $\displaystyle \theta_{k,l}^{(4)}$ are quasi r-Steinberg if and only if
$\displaystyle \theta_{k,l}^{(4)}$ are quasi r-Steinberg if and only if  $(l-k)$ is not invertible in
$(l-k)$ is not invertible in  $\displaystyle \mathbb{Z}_{q-1}, (1+q+q^2)$ is an r-power and
$\displaystyle \mathbb{Z}_{q-1}, (1+q+q^2)$ is an r-power and  $3 \nmid (q-1).$
$3 \nmid (q-1).$3. The characters of type
 $\displaystyle \theta^{(7)}_{t,l}$ are quasi r-Steinberg if and only if r = 7 and q = 2.
$\displaystyle \theta^{(7)}_{t,l}$ are quasi r-Steinberg if and only if r = 7 and q = 2.
Proof. Case I: r = p. Note that ![]() $\displaystyle B = diag(E_2, 1)$ is an r-regular element and its conjugacy class is of type
$\displaystyle B = diag(E_2, 1)$ is an r-regular element and its conjugacy class is of type ![]() $T^{(7)}.$ It follows from the character table of
$T^{(7)}.$ It follows from the character table of ![]() $GL(3,q)$ that any character of type
$GL(3,q)$ that any character of type  $\displaystyle \theta_k^{(2)}$ vanishes on
$\displaystyle \theta_k^{(2)}$ vanishes on ![]() $B.$ Therefore, it is not quasi p-Steinberg. Now note that a character of type
$B.$ Therefore, it is not quasi p-Steinberg. Now note that a character of type  $\theta_k^{(3)}$ takes 0 value only on the conjugacy classes of type
$\theta_k^{(3)}$ takes 0 value only on the conjugacy classes of type ![]() $\displaystyle T^{(2)}, T^{(3)}$ and
$\displaystyle T^{(2)}, T^{(3)}$ and ![]() $T^{(5)}.$ Since there are no p-regular elements in these classes,
$T^{(5)}.$ Since there are no p-regular elements in these classes,  $\theta_k^{(3)}$ is quasi p-Steinberg. Further, any parabolically induced character is not quasi p-Steinberg as it vanishes on the irreducible r-regular element
$\theta_k^{(3)}$ is quasi p-Steinberg. Further, any parabolically induced character is not quasi p-Steinberg as it vanishes on the irreducible r-regular element ![]() $\displaystyle E_n.$
$\displaystyle E_n.$
Case II: r ≠ p. Consider the element  $$ C = \begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{pmatrix}$$. Since its order is
$$ C = \begin{pmatrix}
1 & 1 & 0 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{pmatrix}$$. Since its order is ![]() $p,$ it is r-regular and its conjugacy class is of type
$p,$ it is r-regular and its conjugacy class is of type ![]() $T^{(3)}.$ Since the characters
$T^{(3)}.$ Since the characters  $\displaystyle \theta_k^{(2)}, \theta_k^{(3)}$ and
$\displaystyle \theta_k^{(2)}, \theta_k^{(3)}$ and  $\displaystyle \theta_k^{(5)}$ vanish on
$\displaystyle \theta_k^{(5)}$ vanish on ![]() $T^{(3)},$ they are not quasi r-Steinberg. Now we study the parabolically induced characters
$T^{(3)},$ they are not quasi r-Steinberg. Now we study the parabolically induced characters  $\theta^{(4)}_{k,l},$
$\theta^{(4)}_{k,l},$  $\theta^{(6)}_{k,l,m}$ and
$\theta^{(6)}_{k,l,m}$ and  $\theta^{(7)}_{t,l}.$
$\theta^{(7)}_{t,l}.$
Observe that if ![]() $\displaystyle r \ | \ (q+1),$ then
$\displaystyle r \ | \ (q+1),$ then ![]() $\displaystyle r \ \nmid (q^2+q+1).$ Thus it follows from Lemma 4.2 that no parabolically induced character is quasi r-Steinberg.
$\displaystyle r \ \nmid (q^2+q+1).$ Thus it follows from Lemma 4.2 that no parabolically induced character is quasi r-Steinberg.
Remark 5.2. For an odd prime ![]() $n,$ if a parabolically induced character of
$n,$ if a parabolically induced character of ![]() $GL(n,q)$ is quasi r-Steinberg, then
$GL(n,q)$ is quasi r-Steinberg, then ![]() $\displaystyle r \ \nmid \ (q+1).$
$\displaystyle r \ \nmid \ (q+1).$
Therefore, in the following, we assume that r does not divide ![]() $\displaystyle (q+1):$
$\displaystyle (q+1):$
The characters of type  $\theta^{(6)}_{k,l,m}$
$\theta^{(6)}_{k,l,m}$
Note that the order of the element  $\displaystyle D_1 = diag(\epsilon_2^{(q-1)}, \epsilon_2^{q(q-1)}, 1)$ is
$\displaystyle D_1 = diag(\epsilon_2^{(q-1)}, \epsilon_2^{q(q-1)}, 1)$ is ![]() $(q+1)$. Since
$(q+1)$. Since ![]() $r \ \nmid \ (q+1), D_1$ is an r-regular element. It follows from the character table that any character of type
$r \ \nmid \ (q+1), D_1$ is an r-regular element. It follows from the character table that any character of type  $\theta^{(6)}_{k,l,m}$ vanishes on D 1 and hence is not quasi r-Steinberg.
$\theta^{(6)}_{k,l,m}$ vanishes on D 1 and hence is not quasi r-Steinberg.
The following lemma gives a necessary condition for a parabolically induced character of ![]() $GL(3,q)$ to be quasi r-Steinberg:
$GL(3,q)$ to be quasi r-Steinberg:
Lemma 5.3. Let ![]() $\displaystyle q \geq 3.$ If a parabolically induced character of
$\displaystyle q \geq 3.$ If a parabolically induced character of ![]() $GL(3,q)$ is quasi r-Steinberg, then
$GL(3,q)$ is quasi r-Steinberg, then ![]() $r \ \nmid \ (q-1).$
$r \ \nmid \ (q-1).$
Proof. On contrary, assume that ![]() $\displaystyle q = (1+rm),$ for some
$\displaystyle q = (1+rm),$ for some ![]() $m \in \mathbb{N}$. Then
$m \in \mathbb{N}$. Then ![]() $\displaystyle (1+q+q^2) = (3 + 3rm+r^2m^2).$ Clearly, if r is different from
$\displaystyle (1+q+q^2) = (3 + 3rm+r^2m^2).$ Clearly, if r is different from ![]() $3,$ then
$3,$ then ![]() $r \nmid (1+q+q^2).$ Further, if
$r \nmid (1+q+q^2).$ Further, if ![]() $\displaystyle r=3,$ then
$\displaystyle r=3,$ then ![]() $(1+q+q^2) = 3(1+3(m+m^2)),$ which is not a 3-power. In either case, we get a contradiction to Lemma 4.2.
$(1+q+q^2) = 3(1+3(m+m^2)),$ which is not a 3-power. In either case, we get a contradiction to Lemma 4.2.
In other words, if ![]() $\displaystyle (1+q+q^2)$ is an r-power, then
$\displaystyle (1+q+q^2)$ is an r-power, then ![]() $\displaystyle r \ \nmid \ (q-1).$ Also if
$\displaystyle r \ \nmid \ (q-1).$ Also if ![]() $\displaystyle r \ \nmid \ (q-1),$ then since we have already observed that
$\displaystyle r \ \nmid \ (q-1),$ then since we have already observed that ![]() $\displaystyle r \ \nmid \ (q+1),$ it implies that
$\displaystyle r \ \nmid \ (q+1),$ it implies that ![]() $\displaystyle r \ \nmid (q^2-1)$ as well. With this note, we now continue our investigation:
$\displaystyle r \ \nmid (q^2-1)$ as well. With this note, we now continue our investigation:
The characters of type  $\theta^{(4)}_{k,l}$
$\theta^{(4)}_{k,l}$
It follows from the character table that the classes on which a character of type  $\displaystyle \theta_{k,l}^{(4)}$ can vanish are of type
$\displaystyle \theta_{k,l}^{(4)}$ can vanish are of type ![]() $T^{(5)}$ or
$T^{(5)}$ or ![]() $T^{(6)}.$ Therefore, if the value of
$T^{(6)}.$ Therefore, if the value of  $\displaystyle \theta_{k,l}^{(4)}$ on every r-regular element from these conjugacy classes is non-zero, then it follows from Lemma 4.2 that it is quasi r-Steinberg if and only if
$\displaystyle \theta_{k,l}^{(4)}$ on every r-regular element from these conjugacy classes is non-zero, then it follows from Lemma 4.2 that it is quasi r-Steinberg if and only if ![]() $\displaystyle (1+q+q^2)$ is an r-power.
$\displaystyle (1+q+q^2)$ is an r-power.
Let ![]() $\displaystyle A_{\alpha, \beta}$ and
$\displaystyle A_{\alpha, \beta}$ and ![]() $\displaystyle B_{\alpha, \beta, \gamma}$ be some elements of
$\displaystyle B_{\alpha, \beta, \gamma}$ be some elements of ![]() $GL(3,q)$ whose conjugacy class is of type
$GL(3,q)$ whose conjugacy class is of type ![]() $T^{(5)}$ and
$T^{(5)}$ and ![]() $T^{(6)},$ respectively. Note that
$T^{(6)},$ respectively. Note that  $\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = (\hat{\alpha^{k+l}} \hat{\beta^l} + \hat{\beta^{2l}} \hat{\alpha^k})$ and
$\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = (\hat{\alpha^{k+l}} \hat{\beta^l} + \hat{\beta^{2l}} \hat{\alpha^k})$ and  $\displaystyle \theta_{k,l}^{(4)}(B_{\alpha, \beta, \gamma}) = \hat{\alpha^{k}} \hat{\beta^l} \hat{\gamma^l} + \hat{\alpha^{l}} \hat{\beta^k} \hat{\gamma^l} + \hat{\alpha^{l}} \hat{\beta^l} \hat{\gamma^k}.$ Therefore, if
$\displaystyle \theta_{k,l}^{(4)}(B_{\alpha, \beta, \gamma}) = \hat{\alpha^{k}} \hat{\beta^l} \hat{\gamma^l} + \hat{\alpha^{l}} \hat{\beta^k} \hat{\gamma^l} + \hat{\alpha^{l}} \hat{\beta^l} \hat{\gamma^k}.$ Therefore, if  $\displaystyle \theta_{k,l}^{(4)}$ vanishes on some conjugacy class of type
$\displaystyle \theta_{k,l}^{(4)}$ vanishes on some conjugacy class of type ![]() $T^{(5)}$ or
$T^{(5)}$ or ![]() $T^{(6)},$ then
$T^{(6)},$ then ![]() $F_q^{*}$ contains a primitive second or third root of unity, respectively.
$F_q^{*}$ contains a primitive second or third root of unity, respectively.
Now the following corollary to Lemma 4.2 classifies the quasi r-Steinberg characters of type  $\displaystyle \theta_{k,l}^{(4)}$ of
$\displaystyle \theta_{k,l}^{(4)}$ of ![]() $GL(3,q)$ for even q:
$GL(3,q)$ for even q:
Corollary 5.4. Let q be even. Then  $\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg character of
$\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg character of ![]() $GL(n,q)$ if and only if
$GL(n,q)$ if and only if ![]() $\displaystyle (1+q+q^2)$ is a power of
$\displaystyle (1+q+q^2)$ is a power of ![]() $r.$
$r.$
Proof. Since q is even, ![]() $F_q^{*}$ does not contain the primitive second root of unity and hence
$F_q^{*}$ does not contain the primitive second root of unity and hence  $\displaystyle \theta_{k,l}^{(4)}$ does not vanish on
$\displaystyle \theta_{k,l}^{(4)}$ does not vanish on ![]() $T^{(5)}$. Now we check whether
$T^{(5)}$. Now we check whether ![]() $F_{q}^{*}$ contains a primitive third root of unity. If q is of the form
$F_{q}^{*}$ contains a primitive third root of unity. If q is of the form ![]() $\displaystyle (3m+2),$ then
$\displaystyle (3m+2),$ then ![]() $\displaystyle 3 \ \nmid \ (q-1).$ As
$\displaystyle 3 \ \nmid \ (q-1).$ As ![]() $F_{q}^{*}$ does not have a primitive third root of unity, it follows that
$F_{q}^{*}$ does not have a primitive third root of unity, it follows that  $\displaystyle \theta_{k,l}^{(4)}$ does not vanish on
$\displaystyle \theta_{k,l}^{(4)}$ does not vanish on ![]() $T^{(6)}$. Thus it follows from Lemma 4.2 that
$T^{(6)}$. Thus it follows from Lemma 4.2 that  $\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg if and only if
$\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg if and only if ![]() $\displaystyle (1+q+q^2)$ is a power of
$\displaystyle (1+q+q^2)$ is a power of ![]() $r.$ On the other hand, if
$r.$ On the other hand, if ![]() $\displaystyle q = (3m+1),$ then
$\displaystyle q = (3m+1),$ then ![]() $\displaystyle (1+q+q^2) = 3(1+3m^2+3m)$ is not a prime power. So
$\displaystyle (1+q+q^2) = 3(1+3m^2+3m)$ is not a prime power. So  $\displaystyle \theta_{k,l}^{(4)}$ is not a quasi r-Steinberg character of
$\displaystyle \theta_{k,l}^{(4)}$ is not a quasi r-Steinberg character of ![]() $GL(3,q)$ for such q.
$GL(3,q)$ for such q.
Example. Since ![]() $\displaystyle q=8$ is of the form
$\displaystyle q=8$ is of the form ![]() $(3m+2)$ and
$(3m+2)$ and ![]() $\displaystyle (1+q+q^2) = 73$ is a prime, any character of type
$\displaystyle (1+q+q^2) = 73$ is a prime, any character of type  $\displaystyle \theta_{k,l}^{(4)}$ is a quasi 73-Steinberg character of
$\displaystyle \theta_{k,l}^{(4)}$ is a quasi 73-Steinberg character of ![]() $GL(3,8).$
$GL(3,8).$
Let us now consider the case when q is odd. It follows from Lemma 5.3 that if  $\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg, then
$\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg, then ![]() $\displaystyle r \ \nmid \ (q-1).$ Therefore, the elements in the conjugacy classes of type
$\displaystyle r \ \nmid \ (q-1).$ Therefore, the elements in the conjugacy classes of type ![]() $\displaystyle T^{(4)}, T^{(5)}, T^{(6)}$ and
$\displaystyle T^{(4)}, T^{(5)}, T^{(6)}$ and ![]() $T^{(7)}$ are r-regular.
$T^{(7)}$ are r-regular.
If ![]() $\displaystyle \alpha = \epsilon_1^{s_1}$ and
$\displaystyle \alpha = \epsilon_1^{s_1}$ and ![]() $\displaystyle \beta = \epsilon_1^{s_2}$ are some elements of
$\displaystyle \beta = \epsilon_1^{s_2}$ are some elements of ![]() $F_{q^*}$ with
$F_{q^*}$ with ![]() $\displaystyle 1 \leq s_1 \lt s_2 \leq (q-1),$ then
$\displaystyle 1 \leq s_1 \lt s_2 \leq (q-1),$ then  $\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = \hat{\epsilon_1}^{s_1(k+l)+s_2l} + \hat{\epsilon_1}^{(2s_1l+s_2k)}.$ Therefore,
$\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = \hat{\epsilon_1}^{s_1(k+l)+s_2l} + \hat{\epsilon_1}^{(2s_1l+s_2k)}.$ Therefore,  $\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = 0$ if and only if
$\displaystyle \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = 0$ if and only if  $\displaystyle (s_1-s_2)(k-l) = \frac{(q-1)}{2}.$ It further implies that if k and l are such that
$\displaystyle (s_1-s_2)(k-l) = \frac{(q-1)}{2}.$ It further implies that if k and l are such that ![]() $(k-l)$ is not invertible in
$(k-l)$ is not invertible in ![]() $\mathbb{Z}_{q-1},$ then
$\mathbb{Z}_{q-1},$ then  $\displaystyle \theta_{k,l}^{(4)}$ does not vanish on any element whose conjugacy class is of type
$\displaystyle \theta_{k,l}^{(4)}$ does not vanish on any element whose conjugacy class is of type ![]() $T^{(5)}$. On the other hand, if
$T^{(5)}$. On the other hand, if ![]() $\displaystyle (k-l, q-1) = 1,$ then for the choice of
$\displaystyle (k-l, q-1) = 1,$ then for the choice of  $\displaystyle s_1 = \Big( \frac{q-1}{2(k-l)} + s_2 \Big), \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = 0.$
$\displaystyle s_1 = \Big( \frac{q-1}{2(k-l)} + s_2 \Big), \theta_{k,l}^{(4)}(A_{\alpha, \beta}) = 0.$
Here note that if  $\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg, then
$\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg, then ![]() $\displaystyle 3 \ \nmid \ (q-1).$ Indeed if
$\displaystyle 3 \ \nmid \ (q-1).$ Indeed if ![]() $\displaystyle 3 \ \mid \ (q-1),$ then it follows from a similar discussion as in Corollary 5.4 that
$\displaystyle 3 \ \mid \ (q-1),$ then it follows from a similar discussion as in Corollary 5.4 that ![]() $\displaystyle (1+q+q^2)$ is not an r-power. Thus we obtain the following necessary conditions for
$\displaystyle (1+q+q^2)$ is not an r-power. Thus we obtain the following necessary conditions for  $\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg:
$\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg:
Corollary 5.5. Let q be odd. If a character of type  $\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg character of
$\displaystyle \theta_{k,l}^{(4)}$ is quasi r-Steinberg character of ![]() $GL(3,q),$ then r is the only prime divisor of
$GL(3,q),$ then r is the only prime divisor of ![]() $\displaystyle (1+q+q^2),$
$\displaystyle (1+q+q^2),$ ![]() $(l-k)$ is not invertible in
$(l-k)$ is not invertible in ![]() $\mathbb{Z}_{q-1}$ and
$\mathbb{Z}_{q-1}$ and ![]() $\displaystyle 3 \ \nmid \ (q-1).$
$\displaystyle 3 \ \nmid \ (q-1).$
Now we obtain the sufficient conditions for a character of type  $\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg. Clearly, if
$\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg. Clearly, if ![]() $\displaystyle 3 \nmid (q-1),$ then
$\displaystyle 3 \nmid (q-1),$ then  $\displaystyle \theta_{k,l}^{(4)}(B_{\alpha, \beta, \gamma}) \neq 0 \ \forall \ \alpha, \beta, \gamma \in F_{q}^{*}.$ Therefore, the sufficient conditions for a character
$\displaystyle \theta_{k,l}^{(4)}(B_{\alpha, \beta, \gamma}) \neq 0 \ \forall \ \alpha, \beta, \gamma \in F_{q}^{*}.$ Therefore, the sufficient conditions for a character  $\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg are that r is the only prime divisor of
$\displaystyle \theta_{k,l}^{(4)}$ to be quasi r-Steinberg are that r is the only prime divisor of ![]() $\displaystyle (1+q+q^2),$
$\displaystyle (1+q+q^2),$ ![]() $(l-k)$ is not invertible in
$(l-k)$ is not invertible in ![]() $\mathbb{Z}_{q-1}$ and
$\mathbb{Z}_{q-1}$ and ![]() $\displaystyle 3 \ \nmid \ (q-1).$ It now establishes the parts (i) and (ii) of the Theorem.
$\displaystyle 3 \ \nmid \ (q-1).$ It now establishes the parts (i) and (ii) of the Theorem.
We now make a remark about the existence of infinitely many primes q such that many characters of type  $\displaystyle \theta^{(4)}_{k,l}$ are quasi r-Steinberg characters of
$\displaystyle \theta^{(4)}_{k,l}$ are quasi r-Steinberg characters of ![]() $GL(3,q),$ for some
$GL(3,q),$ for some ![]() $r.$ For instance, in addition to the aforementioned sufficient conditions, let us assume that q is such that
$r.$ For instance, in addition to the aforementioned sufficient conditions, let us assume that q is such that ![]() $\displaystyle 4 \nmid (q-1).$ Since q is odd, it implies that 2 is not invertible in
$\displaystyle 4 \nmid (q-1).$ Since q is odd, it implies that 2 is not invertible in ![]() $\mathbb{Z}_{q-1}.$ Therefore, as a consequence of the above discussion, we have that whenever
$\mathbb{Z}_{q-1}.$ Therefore, as a consequence of the above discussion, we have that whenever  $\displaystyle k = (l+2), \ \theta_{k,l}^{(4)}(A_{\alpha, \beta}) \neq 0 \ \forall \ \alpha, \beta \in F_{q}^{*}.$ This now leads to the following corollary which establishes our remark:
$\displaystyle k = (l+2), \ \theta_{k,l}^{(4)}(A_{\alpha, \beta}) \neq 0 \ \forall \ \alpha, \beta \in F_{q}^{*}.$ This now leads to the following corollary which establishes our remark:
Corollary 5.6. As per Bunyakovsky conjecture there exist infinitely many q for which ![]() $\displaystyle (1+q+q^2)$ is a prime. Then any such q is of the form
$\displaystyle (1+q+q^2)$ is a prime. Then any such q is of the form ![]() $\displaystyle q \not\equiv 1 \mod 12$ and if
$\displaystyle q \not\equiv 1 \mod 12$ and if ![]() $\displaystyle (1+q+q^2) = r$(a prime), then the character
$\displaystyle (1+q+q^2) = r$(a prime), then the character  $\displaystyle \theta^{(4)}_{k,l},$ where
$\displaystyle \theta^{(4)}_{k,l},$ where ![]() $\displaystyle k =(l+2),$ is a quasi r-Steinberg character of
$\displaystyle k =(l+2),$ is a quasi r-Steinberg character of ![]() $GL(3,q).$
$GL(3,q).$
Proof. Bunyakovsky conjecture predicts that there exist infinitely many q for which ![]() $\displaystyle (1+q+q^2)$ is a prime. We first note that such a q cannot be of the form
$\displaystyle (1+q+q^2)$ is a prime. We first note that such a q cannot be of the form ![]() $\displaystyle (12m+1).$ Indeed, then
$\displaystyle (12m+1).$ Indeed, then ![]() $\displaystyle (1+q+q^2) = 3(1+12m(1+4m))$, which cannot be a prime. It implies that for any q for which
$\displaystyle (1+q+q^2) = 3(1+12m(1+4m))$, which cannot be a prime. It implies that for any q for which ![]() $(1+q+q^2)$ is a prime, say
$(1+q+q^2)$ is a prime, say ![]() $r,$
$r,$ ![]() $\displaystyle q \not\equiv 1 \mod(12).$ Now it follows from Corollary 5.5 and the discussion following it, that for any such
$\displaystyle q \not\equiv 1 \mod(12).$ Now it follows from Corollary 5.5 and the discussion following it, that for any such ![]() $q,$
$q,$  $\displaystyle \theta^{(4)}_{l+2,l}$ is a quasi r-Steinberg character of
$\displaystyle \theta^{(4)}_{l+2,l}$ is a quasi r-Steinberg character of ![]() $GL(3,q).$
$GL(3,q).$
The characters of type  $\theta^{(7)}_{t,l}$
$\theta^{(7)}_{t,l}$
It follows from character table that  $\displaystyle \theta^{(7)}_{t,l}$ vanishes on all the conjugacy classes of type
$\displaystyle \theta^{(7)}_{t,l}$ vanishes on all the conjugacy classes of type ![]() $\displaystyle T^{(6)}$ and
$\displaystyle T^{(6)}$ and ![]() $\displaystyle T^{(8)}.$ Now we study the values of
$\displaystyle T^{(8)}.$ Now we study the values of  $\theta^{(7)}_{t,l}$ on the conjugacy classes of type
$\theta^{(7)}_{t,l}$ on the conjugacy classes of type ![]() $T^{(7)}$. Note that for
$T^{(7)}$. Note that for ![]() $\displaystyle E_{i,\alpha} = diag(F_i, \alpha),$ where
$\displaystyle E_{i,\alpha} = diag(F_i, \alpha),$ where  $\displaystyle F_i = diag(\epsilon_2^i, \epsilon_2^{qi})$ is an irreducible in
$\displaystyle F_i = diag(\epsilon_2^i, \epsilon_2^{qi})$ is an irreducible in ![]() $\displaystyle GL(2,q), [E_{i,\alpha}]$ is of type
$\displaystyle GL(2,q), [E_{i,\alpha}]$ is of type ![]() $T^{(7)}$. Here
$T^{(7)}$. Here  $\displaystyle \theta^{(7)}_{t,l}(E_{i,\alpha}) = \hat{\alpha}^t (\hat{\epsilon_2}^{li} + \hat{\epsilon_2}^{lqi}).$ If
$\displaystyle \theta^{(7)}_{t,l}(E_{i,\alpha}) = \hat{\alpha}^t (\hat{\epsilon_2}^{li} + \hat{\epsilon_2}^{lqi}).$ If  $\theta^{(7)}_{t,l}$ vanishes on
$\theta^{(7)}_{t,l}$ vanishes on ![]() $E_{i,\alpha},$ then
$E_{i,\alpha},$ then  $F_{q^2}^{*}$ contains the primitive second root of unity. Note that if
$F_{q^2}^{*}$ contains the primitive second root of unity. Note that if  $\theta^{(7)}_{t,l}$ is quasi r-Steinberg, then
$\theta^{(7)}_{t,l}$ is quasi r-Steinberg, then ![]() $\displaystyle r \ \nmid (q-1)$ (see Lemma 5.3). Now the further discussion is as follows:
$\displaystyle r \ \nmid (q-1)$ (see Lemma 5.3). Now the further discussion is as follows:
• q ≥ 4: Let
 $\displaystyle \alpha, \beta, \gamma$ be distinct elements in
$\displaystyle \alpha, \beta, \gamma$ be distinct elements in  $F_q^{*}.$ Now since
$F_q^{*}.$ Now since  $\theta^{(7)}_{k,l}$ vanishes on the r-regular element
$\theta^{(7)}_{k,l}$ vanishes on the r-regular element  $\displaystyle B_2 = diag(\alpha, \beta, \gamma),$ it is not quasi r-Steinberg.
$\displaystyle B_2 = diag(\alpha, \beta, \gamma),$ it is not quasi r-Steinberg.• q = 2: Note that
 $\displaystyle (1+q+q^2) = 7.$ Since
$\displaystyle (1+q+q^2) = 7.$ Since  $(q-1) = 1,$ there is no element in
$(q-1) = 1,$ there is no element in  $T^{(6)};$ and as
$T^{(6)};$ and as  $F_{2^2}^{*}$ does not contain the primitive second root of unity,
$F_{2^2}^{*}$ does not contain the primitive second root of unity,  $\displaystyle \theta^{(7)}_{t,l}$ does not vanish on
$\displaystyle \theta^{(7)}_{t,l}$ does not vanish on  $T^{(7)}$ either. Since there does not exist any irreducible 7-regular element in
$T^{(7)}$ either. Since there does not exist any irreducible 7-regular element in  $GL(3,2),$ it follows that
$GL(3,2),$ it follows that  $\displaystyle \theta^{(7)}_{t,l}$ is a quasi 7-Steinberg character of
$\displaystyle \theta^{(7)}_{t,l}$ is a quasi 7-Steinberg character of  $GL(3,2).$ Further, if
$GL(3,2).$ Further, if  $\displaystyle r$ is some prime different from
$\displaystyle r$ is some prime different from  $7,$ then it follows from Lemma 4.2 that
$7,$ then it follows from Lemma 4.2 that  $\displaystyle \theta^{(7)}_{t,l}$ is not quasi r-Steinberg.
$\displaystyle \theta^{(7)}_{t,l}$ is not quasi r-Steinberg.• q = 3: In this case,
 $(1+q+q^2) = 13$. Note that the element
$(1+q+q^2) = 13$. Note that the element  $\displaystyle E_{2,1} = diag(F_1, 1),$ where
$\displaystyle E_{2,1} = diag(F_1, 1),$ where  $\displaystyle F_1 = diag(\epsilon_2^2, \epsilon_2^{6}),$ is a 13-regular element whose class is of type
$\displaystyle F_1 = diag(\epsilon_2^2, \epsilon_2^{6}),$ is a 13-regular element whose class is of type  $T^{(7)}.$ Since
$T^{(7)}.$ Since  $\displaystyle \theta^{(7)}_{t,l}$ vanishes on
$\displaystyle \theta^{(7)}_{t,l}$ vanishes on  $\displaystyle E_{2,1}$, it is not quasi 13-Steinberg. Now one can conclude from Lemma 4.2 that
$\displaystyle E_{2,1}$, it is not quasi 13-Steinberg. Now one can conclude from Lemma 4.2 that  $\displaystyle \theta^{(7)}_{t,l}$ is not a quasi r-Steinberg character of
$\displaystyle \theta^{(7)}_{t,l}$ is not a quasi r-Steinberg character of  $GL(3,3),$ for any r.
$GL(3,3),$ for any r.
6. Weak Steinberg characters of general linear groups
In this section, we classify the weak r-Steinberg characters of ![]() $GL(n,q).$ Towards this end, we first make the following remark:
$GL(n,q).$ Towards this end, we first make the following remark:
Remark 6.1. If ![]() $\displaystyle \chi$ is a weak r-Steinberg character of
$\displaystyle \chi$ is a weak r-Steinberg character of ![]() $\displaystyle GL(n,q),$ then
$\displaystyle GL(n,q),$ then ![]() $\displaystyle r \ \nmid \ (q-1).$ Indeed if
$\displaystyle r \ \nmid \ (q-1).$ Indeed if ![]() $\displaystyle r \ \mid \ (q-1),$ then the central elements
$\displaystyle r \ \mid \ (q-1),$ then the central elements ![]() $\displaystyle \alpha I_n,$ where
$\displaystyle \alpha I_n,$ where ![]() $\displaystyle 1 \neq \alpha \in F_q^{*},$ are r-singular. It implies that
$\displaystyle 1 \neq \alpha \in F_q^{*},$ are r-singular. It implies that ![]() $\displaystyle \chi(\alpha I_n) = 0,$ which is a contradiction.
$\displaystyle \chi(\alpha I_n) = 0,$ which is a contradiction.
Recall that by definition, a weak r-Steinberg character is quasi r-Steinberg. In the following, we first determine which quasi r-Steinberg characters of ![]() $GL(2,q)$ and
$GL(2,q)$ and ![]() $GL(3,q)$ are weak r-Steinberg:
$GL(3,q)$ are weak r-Steinberg:
Lemma 6.2. Let ![]() $\displaystyle q \geq 3$ be a prime power. Then a nonlinear quasi r-Steinberg character χ of
$\displaystyle q \geq 3$ be a prime power. Then a nonlinear quasi r-Steinberg character χ of ![]() $GL(2,q)$ is weak r-Steinberg if and only if one of the following holds:
$GL(2,q)$ is weak r-Steinberg if and only if one of the following holds:
1. χ is of type
 $\chi_k^{(2)}$ and
$\chi_k^{(2)}$ and  $r=p.$
$r=p.$2. χ is a parabolically induced character and
 $(q{+}1)$ is an r-power, for some odd prime r.
$(q{+}1)$ is an r-power, for some odd prime r.
Proof. Note that ![]() $|Syl_p(GL(2,q))| = q.$ If
$|Syl_p(GL(2,q))| = q.$ If ![]() $r=p,$ then the characters of type
$r=p,$ then the characters of type  $\chi_k^{(2)}$ are weak p-Steinberg as their degree is q and they vanish on all p-singular elements of
$\chi_k^{(2)}$ are weak p-Steinberg as their degree is q and they vanish on all p-singular elements of ![]() $GL(2,q)$. Now we consider the case when r is some prime other than
$GL(2,q)$. Now we consider the case when r is some prime other than ![]() $p.$ In this direction, first recall that a cuspidal character of
$p.$ In this direction, first recall that a cuspidal character of ![]() $GL(2,q)$ is quasi r-Steinberg if and only if
$GL(2,q)$ is quasi r-Steinberg if and only if ![]() $\displaystyle (q-1) = r^{\beta}.$ Since
$\displaystyle (q-1) = r^{\beta}.$ Since ![]() $\displaystyle |GL(2,q)|= q(q-1)^2(q+1), |Syl_r(GL(2,q))| \geq (q-1)^2.$ Since the degree of a cuspidal character is
$\displaystyle |GL(2,q)|= q(q-1)^2(q+1), |Syl_r(GL(2,q))| \geq (q-1)^2.$ Since the degree of a cuspidal character is ![]() $(q-1)$, it is not weak r-Steinberg.
$(q-1)$, it is not weak r-Steinberg.
Further, note that it follows from Theorem 4.3 that a parabolically induced character ![]() $\displaystyle \chi_{k,l}$ is quasi r-Steinberg if and only if its degree,
$\displaystyle \chi_{k,l}$ is quasi r-Steinberg if and only if its degree, ![]() $\displaystyle (q+1),$ is an r-power. If
$\displaystyle (q+1),$ is an r-power. If ![]() $r=2,$ then
$r=2,$ then ![]() $ (q-1)$ is also divisible by 2 and hence
$ (q-1)$ is also divisible by 2 and hence ![]() $\displaystyle \chi_{k,l}(1) \neq |Syl_r(GL(2,q))|.$ On the other hand, if
$\displaystyle \chi_{k,l}(1) \neq |Syl_r(GL(2,q))|.$ On the other hand, if ![]() $\displaystyle r \neq 2,$ then q is even and
$\displaystyle r \neq 2,$ then q is even and ![]() $\displaystyle \chi_{k,l}(1) = |Syl_r(GL(2,q))|.$ Since there does not exist any r-singular element in
$\displaystyle \chi_{k,l}(1) = |Syl_r(GL(2,q))|.$ Since there does not exist any r-singular element in ![]() $C^{(1)}, C^{(2)}$ and
$C^{(1)}, C^{(2)}$ and ![]() $C^{(3)},$
$C^{(3)},$ ![]() $\displaystyle \chi_{k,l}$ is r-vanishing too. Hence the result follows.
$\displaystyle \chi_{k,l}$ is r-vanishing too. Hence the result follows.
Lemma 6.3. A cuspidal character of ![]() $GL(3,q)$ is weak r-Steinberg if and only if q = 2 and r = 3. Otherwise, an irreducible nonlinear character of
$GL(3,q)$ is weak r-Steinberg if and only if q = 2 and r = 3. Otherwise, an irreducible nonlinear character of ![]() $GL(3,q)$ is weak r-Steinberg if and only if it is quasi r-Steinberg.
$GL(3,q)$ is weak r-Steinberg if and only if it is quasi r-Steinberg.
Proof. Since the degree of a cuspidal character is ![]() $\displaystyle (q-1)(q^2-1),$ it follows from Theorem 1.2 that a quasi r-Steinberg cuspidal character of
$\displaystyle (q-1)(q^2-1),$ it follows from Theorem 1.2 that a quasi r-Steinberg cuspidal character of ![]() $GL(3,q)$ has a prime power degree if and only if
$GL(3,q)$ has a prime power degree if and only if ![]() $(q,r) \in \{(3,2), (2,3)\}.$ If
$(q,r) \in \{(3,2), (2,3)\}.$ If ![]() $q=3,$ then since
$q=3,$ then since ![]() $2 \ | \ (3-1),$ it follows from Remark 6.1 that no cuspidal character of
$2 \ | \ (3-1),$ it follows from Remark 6.1 that no cuspidal character of ![]() $GL(3,3)$ is weak 2-Steinberg. Further, if
$GL(3,3)$ is weak 2-Steinberg. Further, if ![]() $q=2,$ then the degree of a cuspidal character of
$q=2,$ then the degree of a cuspidal character of ![]() $GL(3,2)$ is 4 which is
$GL(3,2)$ is 4 which is ![]() $|Syl_3(GL(3,2))|.$ Now since any cuspidal character of
$|Syl_3(GL(3,2))|.$ Now since any cuspidal character of ![]() $GL(3,2)$ is 3-vanishing, it is weak 3-Steinberg. Hence the first part of result is established.
$GL(3,2)$ is 3-vanishing, it is weak 3-Steinberg. Hence the first part of result is established.
Observe that the degree of a character of type  $\theta_k^{(2)}$ is not a prime power and that any character of type
$\theta_k^{(2)}$ is not a prime power and that any character of type  $\theta_k^{(3)}$ is weak r-Steinberg if and only if
$\theta_k^{(3)}$ is weak r-Steinberg if and only if ![]() $r=p.$ Recall that if a parabolically induced character of
$r=p.$ Recall that if a parabolically induced character of ![]() $GL(3,q)$ is quasi r-Steinberg, then
$GL(3,q)$ is quasi r-Steinberg, then ![]() $(1+q+q^2)$ is an r-power. It follows that
$(1+q+q^2)$ is an r-power. It follows that ![]() $r \neq p.$
$r \neq p.$
Assume that the integers ![]() $k, l$ and t are such that the characters
$k, l$ and t are such that the characters  $\displaystyle \theta_{k,l}^{(4)}$ and
$\displaystyle \theta_{k,l}^{(4)}$ and  $\displaystyle \theta_{t,l}^{(7)}$ are quasi r-Steinberg (c.f. Theorem 5.1). Since they satisfy the degree condition, we check whether they are r-vanishing or not. It follows from Lemma 5.3 that
$\displaystyle \theta_{t,l}^{(7)}$ are quasi r-Steinberg (c.f. Theorem 5.1). Since they satisfy the degree condition, we check whether they are r-vanishing or not. It follows from Lemma 5.3 that ![]() $\displaystyle r \ \nmid \ (q-1)$ and hence no element in the classes of type
$\displaystyle r \ \nmid \ (q-1)$ and hence no element in the classes of type ![]() $\displaystyle \{T^{(i)} \ | \ 1 \leq i \leq 6 \}$ is r-singular. Further, if
$\displaystyle \{T^{(i)} \ | \ 1 \leq i \leq 6 \}$ is r-singular. Further, if ![]() $\displaystyle r \ | \ (q+1),$ then no parabolically induced character of
$\displaystyle r \ | \ (q+1),$ then no parabolically induced character of ![]() $GL(3,q)$ is quasi r-Steinberg. Therefore,
$GL(3,q)$ is quasi r-Steinberg. Therefore, ![]() $\displaystyle r \ \nmid \ (q^2-1).$ It implies that no element in any class of type
$\displaystyle r \ \nmid \ (q^2-1).$ It implies that no element in any class of type ![]() $\displaystyle T^{(7)}$ is r-singular. Moreover, as r is a divisor of
$\displaystyle T^{(7)}$ is r-singular. Moreover, as r is a divisor of ![]() $GL(3,q),$ it follows that
$GL(3,q),$ it follows that ![]() $r \ | \ (q^3-1).$ Hence
$r \ | \ (q^3-1).$ Hence ![]() $GL(3,q)$ has irreducible r-singular elements. Since
$GL(3,q)$ has irreducible r-singular elements. Since  $\displaystyle \theta_{k,l}^{(4)}$ and
$\displaystyle \theta_{k,l}^{(4)}$ and  $\displaystyle \theta_{t,l}^{(7)}$ vanish on them, they are r-vanishing. Therefore, the quasi r-Steinberg parabolically induced characters of
$\displaystyle \theta_{t,l}^{(7)}$ vanish on them, they are r-vanishing. Therefore, the quasi r-Steinberg parabolically induced characters of ![]() $GL(3,q)$ are weak r-Steinberg.
$GL(3,q)$ are weak r-Steinberg.
Now we characterize the weak r-Steinberg characters of ![]() $GL(n,q).$ Recall that an irreducible character χ of
$GL(n,q).$ Recall that an irreducible character χ of ![]() $\displaystyle GL(n,q)$ is of the form
$\displaystyle GL(n,q)$ is of the form  $\displaystyle (g_1^{n_1} g_2^{n_2} \ldots g_k^{n_k}),$ where for any
$\displaystyle (g_1^{n_1} g_2^{n_2} \ldots g_k^{n_k}),$ where for any ![]() $\displaystyle 1 \leq i \leq k,$ the degree of the simplex gi is
$\displaystyle 1 \leq i \leq k,$ the degree of the simplex gi is ![]() $\displaystyle d_i$ and
$\displaystyle d_i$ and  $\displaystyle \sum_{i=1}^{k} d_i n_i = n$ (see [Reference Green6]). Further, it follows from [Reference Darafsheh4] that if the degree of χ is some prime power, then
$\displaystyle \sum_{i=1}^{k} d_i n_i = n$ (see [Reference Green6]). Further, it follows from [Reference Darafsheh4] that if the degree of χ is some prime power, then
 \begin{equation}
\chi(1) = \frac{\psi_n(q)}{\psi_{n_1}(q^{d_1}) \psi_{n_2}(q^{d_2}) \ldots \psi_{n_k}(q^{d_k})},
\end{equation}
\begin{equation}
\chi(1) = \frac{\psi_n(q)}{\psi_{n_1}(q^{d_1}) \psi_{n_2}(q^{d_2}) \ldots \psi_{n_k}(q^{d_k})},
\end{equation} where  $\displaystyle \psi_{x}(q^{y}) = \prod_{i=1}^{x} (q^{iy}-1).$ Now we state the Zsigmondy’s theorem (see Theorem 3 in [Reference Roitman14]), which is crucial to the upcoming discussion.
$\displaystyle \psi_{x}(q^{y}) = \prod_{i=1}^{x} (q^{iy}-1).$ Now we state the Zsigmondy’s theorem (see Theorem 3 in [Reference Roitman14]), which is crucial to the upcoming discussion.
Let a and l be integers greater than 1. Then there exists a prime divisor s of ![]() $\displaystyle (a^l-1)$ such that
$\displaystyle (a^l-1)$ such that ![]() $\displaystyle s \ \nmid \ (a^k-1) \ \forall \ 0 \lt k \lt l$, except exactly in the following cases:
$\displaystyle s \ \nmid \ (a^k-1) \ \forall \ 0 \lt k \lt l$, except exactly in the following cases:
•
 $\displaystyle l = 2, a = (2^t - 1),$ where
$\displaystyle l = 2, a = (2^t - 1),$ where  $\displaystyle t \geq 2.$
$\displaystyle t \geq 2.$•
 $\displaystyle l = 6, a = 2.$
$\displaystyle l = 6, a = 2.$
We are now in a position to classify the weak r-Steinberg characters of ![]() $GL(n,q):$
$GL(n,q):$
Proof of Theorem 1.2:
Let χ be a weak r-Steinberg character of ![]() $GL(n,q).$ Since
$GL(n,q).$ Since ![]() $\displaystyle r \neq p, \ \chi(1) = |(q^n-1)(q^{n-1}-1) \ldots (q-1)|_r.$ The following cases arise:
$\displaystyle r \neq p, \ \chi(1) = |(q^n-1)(q^{n-1}-1) \ldots (q-1)|_r.$ The following cases arise:
Case I: ![]() $\displaystyle r \nmid (q^n-1).$ By Zsigmondy’s theorem there exists a prime divisor s of
$\displaystyle r \nmid (q^n-1).$ By Zsigmondy’s theorem there exists a prime divisor s of ![]() $\displaystyle (q^n-1)$ such that
$\displaystyle (q^n-1)$ such that ![]() $\displaystyle s \ \nmid \ (q^m-1) \ \forall \ m \lt n;$ except for
$\displaystyle s \ \nmid \ (q^m-1) \ \forall \ m \lt n;$ except for ![]() $\displaystyle (n, q) = (2, 2^t - 1)$ and
$\displaystyle (n, q) = (2, 2^t - 1)$ and ![]() $(6, 2).$ Clearly, s is different from
$(6, 2).$ Clearly, s is different from ![]() $r.$ Since
$r.$ Since ![]() $\displaystyle \chi(1)$ is an r-power and
$\displaystyle \chi(1)$ is an r-power and ![]() $\displaystyle s \mid (q^n-1),$ it follows from (6.1) that there exists some
$\displaystyle s \mid (q^n-1),$ it follows from (6.1) that there exists some ![]() $\displaystyle 1 \leq j \leq k$ such that
$\displaystyle 1 \leq j \leq k$ such that  $\displaystyle s \ | \ \psi_{n_j}(q^{d_j}).$ Without loss of generality, assume that j = 1. Since s is a prime, s divides
$\displaystyle s \ | \ \psi_{n_j}(q^{d_j}).$ Without loss of generality, assume that j = 1. Since s is a prime, s divides ![]() $\displaystyle (q^{id_1}-1)$ for some
$\displaystyle (q^{id_1}-1)$ for some ![]() $\displaystyle 1 \leq i \leq n_1.$ As
$\displaystyle 1 \leq i \leq n_1.$ As ![]() $\displaystyle s \ \nmid \ (q^m-1) \ \forall \ m \lt n,$ it implies that
$\displaystyle s \ \nmid \ (q^m-1) \ \forall \ m \lt n,$ it implies that ![]() $id_1 \gt (n-1).$ Thus
$id_1 \gt (n-1).$ Thus ![]() $n_1d_1=n.$ Also note that
$n_1d_1=n.$ Also note that ![]() $d_1 = 1$ implies that
$d_1 = 1$ implies that ![]() $\chi(1) = 1$. So
$\chi(1) = 1$. So ![]() $d_1 \geq 2.$
$d_1 \geq 2.$
If ![]() $\displaystyle n=2,$ then
$\displaystyle n=2,$ then ![]() $\displaystyle r \ | \ (q^2-1).$ But since
$\displaystyle r \ | \ (q^2-1).$ But since ![]() $\displaystyle r \nmid (q^n-1),$ it follows that
$\displaystyle r \nmid (q^n-1),$ it follows that ![]() $\displaystyle n \geq 3.$ First assume that n = 3. If
$\displaystyle n \geq 3.$ First assume that n = 3. If ![]() $\displaystyle r \nmid (q^3-1),$ then it follows from Lemma 4.2 that χ is not a parabolically induced character. Also, Lemma 6.3 implies that the cuspidal characters of
$\displaystyle r \nmid (q^3-1),$ then it follows from Lemma 4.2 that χ is not a parabolically induced character. Also, Lemma 6.3 implies that the cuspidal characters of ![]() $GL(3,2)$ are weak r-Steinberg if and only if r = 3. Further, note that it follows from Equation (6.2) that the only choice of
$GL(3,2)$ are weak r-Steinberg if and only if r = 3. Further, note that it follows from Equation (6.2) that the only choice of ![]() $\displaystyle (n,q)$ for which
$\displaystyle (n,q)$ for which ![]() $\chi(1)$ is a prime power is
$\chi(1)$ is a prime power is ![]() $(4,2)$. The only character in the character table of
$(4,2)$. The only character in the character table of ![]() $GL(4,2)$ whose degree is a prime power is the character of degree 7. But this character is not quasi 7-Steinberg.
$GL(4,2)$ whose degree is a prime power is the character of degree 7. But this character is not quasi 7-Steinberg.
If ![]() $\displaystyle (n, q) = (2, 2^t - 1),$ it follows from Lemma 6.2 that χ is not weak r-Steinberg. Now assume that
$\displaystyle (n, q) = (2, 2^t - 1),$ it follows from Lemma 6.2 that χ is not weak r-Steinberg. Now assume that ![]() $\displaystyle (n, q) = (6, 2).$ Since
$\displaystyle (n, q) = (6, 2).$ Since ![]() $GL(6,2)$ is a quasi-simple group, it follows from Theorem 1.2 in [Reference Malle and Zalesskii10] that
$GL(6,2)$ is a quasi-simple group, it follows from Theorem 1.2 in [Reference Malle and Zalesskii10] that ![]() $GL(6,2)$ does not have any character whose degree is a prime power.
$GL(6,2)$ does not have any character whose degree is a prime power.
Case II: ![]() $\displaystyle r \mid (q^n-1).$ Since
$\displaystyle r \mid (q^n-1).$ Since ![]() $\displaystyle r \nmid (q-1)$, we have that
$\displaystyle r \nmid (q-1)$, we have that ![]() $\displaystyle r \nmid (q^{n-1}-1).$ In this case, the previous argument for a = q and
$\displaystyle r \nmid (q^{n-1}-1).$ In this case, the previous argument for a = q and ![]() $l=(n-1)$ yields that k = 2 and g 1 is a simplex of degree d 1 with
$l=(n-1)$ yields that k = 2 and g 1 is a simplex of degree d 1 with ![]() $\displaystyle n_1d_1=(n-1),$ where q and n are such that
$\displaystyle n_1d_1=(n-1),$ where q and n are such that ![]() $\displaystyle (q, n-1) \notin \{(2^t - 1, 2), (2,6) \}.$ Clearly, the degree of g 2 is 1 and hence the degree of χ is
$\displaystyle (q, n-1) \notin \{(2^t - 1, 2), (2,6) \}.$ Clearly, the degree of g 2 is 1 and hence the degree of χ is
 \begin{equation}
\frac{(q^n-1)(q^{n-1}-1)\ldots(q-1)}{(q^{d_1}-1)(q^{2d_1}-1)\ldots(q^{n_1d_1}-1)(q-1)} = (q^n-1)(q^{n-2}-1)\ldots(q^{n-d_1}-1).
\end{equation}
\begin{equation}
\frac{(q^n-1)(q^{n-1}-1)\ldots(q-1)}{(q^{d_1}-1)(q^{2d_1}-1)\ldots(q^{n_1d_1}-1)(q-1)} = (q^n-1)(q^{n-2}-1)\ldots(q^{n-d_1}-1).
\end{equation} If ![]() $\displaystyle n=2,$ then the degree of
$\displaystyle n=2,$ then the degree of ![]() $\chi,$
$\chi,$ ![]() $\chi(1) = (q+1).$ It follows from Lemma 6.2 that χ is weak r-Steinberg if and only if
$\chi(1) = (q+1).$ It follows from Lemma 6.2 that χ is weak r-Steinberg if and only if ![]() $(q+1)=r^{\beta},$ for an odd prime
$(q+1)=r^{\beta},$ for an odd prime ![]() $r.$ Further, if
$r.$ Further, if ![]() $\displaystyle n=3,$ then we have the following:
$\displaystyle n=3,$ then we have the following:
1. If
 $d_1 = 1,$ then
$d_1 = 1,$ then  $\chi(1) = (q^2+q+1)$;
$\chi(1) = (q^2+q+1)$;2. If
 $d_1 = 2,$ then
$d_1 = 2,$ then  $\displaystyle \chi(1) = (q^3-1).$
$\displaystyle \chi(1) = (q^3-1).$
Now Lemma 6.3 gives the conditions under which the characters of these degrees are weak r-Steinberg. Finally, assume that ![]() $n \geq 4.$ If
$n \geq 4.$ If ![]() $d_1 \geq 2,$ then both
$d_1 \geq 2,$ then both ![]() $(q^n-1)$ and
$(q^n-1)$ and ![]() $(q^{n-2}-1)$ occur as divisors of
$(q^{n-2}-1)$ occur as divisors of ![]() $\chi(1)$ and hence are r-powers. This contradicts the fact that
$\chi(1)$ and hence are r-powers. This contradicts the fact that ![]() $\displaystyle r \ \nmid \ (q-1).$ Therefore,
$\displaystyle r \ \nmid \ (q-1).$ Therefore, ![]() $\displaystyle d_1 = 1$ and hence
$\displaystyle d_1 = 1$ and hence ![]() $\displaystyle \chi = (g_1^{n-1}g_2)$ has degree
$\displaystyle \chi = (g_1^{n-1}g_2)$ has degree  $\displaystyle \chi(1) = \frac{q^n-1}{q-1}.$ Since
$\displaystyle \chi(1) = \frac{q^n-1}{q-1}.$ Since
it further implies that ![]() $\displaystyle r \ \nmid \ (q^i-1),$ for any
$\displaystyle r \ \nmid \ (q^i-1),$ for any ![]() $\displaystyle 1 \leq i \leq (n-1).$
$\displaystyle 1 \leq i \leq (n-1).$
Note that if ![]() $\displaystyle n \geq 4$ is an even integer, then
$\displaystyle n \geq 4$ is an even integer, then ![]() $\displaystyle diag(E_2, E_2, \ldots, E_2) \notin P_{n-1,1}$. Further, if
$\displaystyle diag(E_2, E_2, \ldots, E_2) \notin P_{n-1,1}$. Further, if ![]() $\displaystyle n \geq 5$ is an odd integer, then
$\displaystyle n \geq 5$ is an odd integer, then ![]() $\displaystyle diag(E_3, E_2, \ldots, E_2)$ intersects
$\displaystyle diag(E_3, E_2, \ldots, E_2)$ intersects ![]() $\displaystyle P_{n-1,1}$ trivially. Since in either case χ vanishes on some r-regular element, it is not weak r-Steinberg.
$\displaystyle P_{n-1,1}$ trivially. Since in either case χ vanishes on some r-regular element, it is not weak r-Steinberg.
Now if ![]() $\displaystyle (n-1, q) = (2, 2^t - 1),$ then n = 3. The weak Steinberg characters of
$\displaystyle (n-1, q) = (2, 2^t - 1),$ then n = 3. The weak Steinberg characters of ![]() $GL(3,q)$ have been classified in Lemma 6.3. If
$GL(3,q)$ have been classified in Lemma 6.3. If ![]() $\displaystyle (n-1, q) = (6, 2),$ then since r is a divisor of
$\displaystyle (n-1, q) = (6, 2),$ then since r is a divisor of ![]() $\displaystyle (2^7-1),$
$\displaystyle (2^7-1),$ ![]() $\displaystyle r = 127.$ Now note that it follows from the character table that
$\displaystyle r = 127.$ Now note that it follows from the character table that ![]() $GL(7,2)$ does not have a character of degree 127. Now the result follows.
$GL(7,2)$ does not have a character of degree 127. Now the result follows.
Acknowledgements
The author is grateful to Prof. Pooja Singla for the encouragement to take up the project and for the discussions throughout. The author is also thankful to the referee for the careful review and comments, which have greatly improved the presentation of this work.
Competing interest
There is no conflict of interest to declare.
Appendix
In the following, we give the character tables of ![]() $GL(2,q)$ and
$GL(2,q)$ and ![]() $GL(3,q)$. Note that in these tables, Class and Rep denote the type and the representative of conjugacy class.
$GL(3,q)$. Note that in these tables, Class and Rep denote the type and the representative of conjugacy class.
Table A1. Character table of ![]() $GL(2,q)$.
$GL(2,q)$.

where in this table:
•
 $\alpha, \beta \in F_q^{*}$ such that
$\alpha, \beta \in F_q^{*}$ such that  $\alpha \neq \beta.$
$\alpha \neq \beta.$•
 $y \in F_{q^2} \setminus F_q; y^q$ is excluded whenever y is included.
$y \in F_{q^2} \setminus F_q; y^q$ is excluded whenever y is included.
Table A2. Character table of ![]() $GL(3,q)$.
$GL(3,q)$.




where in this table:
•
 $\alpha, \beta, \gamma \in F_q^{*}$ such that
$\alpha, \beta, \gamma \in F_q^{*}$ such that  $\alpha \neq \beta \neq \gamma \neq \alpha.$
$\alpha \neq \beta \neq \gamma \neq \alpha.$•
 $x \in F_{q^2} \setminus F_q; x^q$ is excluded whenever x is included.
$x \in F_{q^2} \setminus F_q; x^q$ is excluded whenever x is included.•
 $s \in F_{q^3} \setminus F_q; s^q$ and
$s \in F_{q^3} \setminus F_q; s^q$ and  $s^{q^2}$ are excluded whenever s is included.
$s^{q^2}$ are excluded whenever s is included.