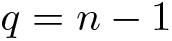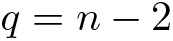1. Introduction
One of the most central results in the theory of lattices is Margulis’ Normal Subgroup Theorem for irreducible lattices in connected semi-simple Lie groups of real rank ![]() $\geq 2$ with a finite centre and no non-trivial compact factor [Reference Margulis16]. Among all the recent generalizations, let us mention that Bader and Shalom proved a version of the Normal Subgroup Theorem for irreducible cocompact lattices in a product of two locally compact, non-discrete, compactly generated groups [Reference Bader and Shalom3]. Based on earlier results in [Reference Rémy18], Caprace and Rémy applied the Normal Subgroup Theorem to show simplicity for Kac–Moody groups over finite fields of irreducible, non-spherical and non-affine types that are twin building lattices (cf. [Reference Caprace and Rémy10, Theorems 18, 19, 20]). Moreover, it can be used to prove virtual simplicity of certain twin tree lattices with non-trivial commutation relations (cf. [Reference Caprace and Rémy11]).
$\geq 2$ with a finite centre and no non-trivial compact factor [Reference Margulis16]. Among all the recent generalizations, let us mention that Bader and Shalom proved a version of the Normal Subgroup Theorem for irreducible cocompact lattices in a product of two locally compact, non-discrete, compactly generated groups [Reference Bader and Shalom3]. Based on earlier results in [Reference Rémy18], Caprace and Rémy applied the Normal Subgroup Theorem to show simplicity for Kac–Moody groups over finite fields of irreducible, non-spherical and non-affine types that are twin building lattices (cf. [Reference Caprace and Rémy10, Theorems 18, 19, 20]). Moreover, it can be used to prove virtual simplicity of certain twin tree lattices with non-trivial commutation relations (cf. [Reference Caprace and Rémy11]).
In [Reference Rémy17] and [Reference Carbone and Garland12], Rémy, and independently Carbone and Garland, proved that certain groups acting on (twin) buildings are lattices. To be more precise: Let (W, S) be a Coxeter system with ![]() $\vert S \vert \lt \infty$, and let
$\vert S \vert \lt \infty$, and let ![]() $\Phi := \Phi(W, S)$ be its associated set of roots (viewed as half-spaces). Let
$\Phi := \Phi(W, S)$ be its associated set of roots (viewed as half-spaces). Let ![]() $\mathcal{D} = (G, (U_{\alpha})_{\alpha \in \Phi})$ be an RGD system of type (W, S), i.e. a group G together with a family
$\mathcal{D} = (G, (U_{\alpha})_{\alpha \in \Phi})$ be an RGD system of type (W, S), i.e. a group G together with a family ![]() $(U_{\alpha})_{\alpha \in \Phi}$ of subgroups (which we call root groups) indexed by the set of roots Φ satisfying some combinatorial axioms (for the precise definition, we refer to [Reference Abramenko and Brown1, Ch. 7,8]). Then, there exists a twin building
$(U_{\alpha})_{\alpha \in \Phi}$ of subgroups (which we call root groups) indexed by the set of roots Φ satisfying some combinatorial axioms (for the precise definition, we refer to [Reference Abramenko and Brown1, Ch. 7,8]). Then, there exists a twin building ![]() $\Delta = (\Delta_+, \Delta_-, \delta_*)$ such that G acts on Δ. It turns out that under some conditions,
$\Delta = (\Delta_+, \Delta_-, \delta_*)$ such that G acts on Δ. It turns out that under some conditions,  $G^{\dagger} := \langle U_{\alpha} \mid \alpha \in \Phi \rangle \leq \operatorname{Aut}(\Delta_+) \times \operatorname{Aut}(\Delta_-)$ and
$G^{\dagger} := \langle U_{\alpha} \mid \alpha \in \Phi \rangle \leq \operatorname{Aut}(\Delta_+) \times \operatorname{Aut}(\Delta_-)$ and ![]() $U_+ := \langle U_{\alpha} \mid \alpha \in \Phi_+ \rangle \leq \operatorname{Aut}(\Delta_-)$ are lattices (cf. [Reference Rémy17], [Reference Carbone and Garland12]) – and in this case
$U_+ := \langle U_{\alpha} \mid \alpha \in \Phi_+ \rangle \leq \operatorname{Aut}(\Delta_-)$ are lattices (cf. [Reference Rémy17], [Reference Carbone and Garland12]) – and in this case ![]() $G^{\dagger}$ is an example of a twin building lattice. Sufficient conditions are that every root group is finite, W is infinite and for
$G^{\dagger}$ is an example of a twin building lattice. Sufficient conditions are that every root group is finite, W is infinite and for ![]() $q_{\min} := \min\{\vert U_{\alpha} \vert \mid \alpha \in \Phi \}$, one has
$q_{\min} := \min\{\vert U_{\alpha} \vert \mid \alpha \in \Phi \}$, one has  $p_{(W, S)}\left( \frac{1}{q_{\min}} \right) \lt \infty$, where
$p_{(W, S)}\left( \frac{1}{q_{\min}} \right) \lt \infty$, where  $p_{(W, S)}(t)$ denotes the growth function of (W, S). Some authors call
$p_{(W, S)}(t)$ denotes the growth function of (W, S). Some authors call  $p_{(W, S)}(t)$ the (spherical) growth series (cf. [Reference Davis13, Chapter 17] or [Reference de la Harpe14, Chapter VI]) or the Poincaré series of (W, S) (cf. [Reference Björner and Brenti6, Chapter 7.1]). It is clear that
$p_{(W, S)}(t)$ the (spherical) growth series (cf. [Reference Davis13, Chapter 17] or [Reference de la Harpe14, Chapter VI]) or the Poincaré series of (W, S) (cf. [Reference Björner and Brenti6, Chapter 7.1]). It is clear that  $p_{(W, S)}\left( \frac{1}{q_{\min}} \right) \lt \infty$ holds if
$p_{(W, S)}\left( \frac{1}{q_{\min}} \right) \lt \infty$ holds if ![]() $\vert S \vert \leq q_{\min}$. It is particularly unsatisfying that the criterion
$\vert S \vert \leq q_{\min}$. It is particularly unsatisfying that the criterion ![]() $\vert S \vert \leq q_{\min}$ does not apply to Coxeter systems of rank
$\vert S \vert \leq q_{\min}$ does not apply to Coxeter systems of rank ![]() $n \geq 3$ and
$n \geq 3$ and ![]() $q_{\min} = 2$. However, there are examples of Coxeter systems (W, S) of rank
$q_{\min} = 2$. However, there are examples of Coxeter systems (W, S) of rank ![]() $n \geq 3$ with
$n \geq 3$ with  $p_{(W, S)}\left( \frac{1}{2} \right) \lt \infty$. Note that the growth function
$p_{(W, S)}\left( \frac{1}{2} \right) \lt \infty$. Note that the growth function  $p_{(W, S)}(t)$ applied to q −1 with
$p_{(W, S)}(t)$ applied to q −1 with ![]() $q\in \mathbb{N}$ and
$q\in \mathbb{N}$ and ![]() $q\geq 2$ is finite for spherical and affine Coxeter systems (cf. [Reference Bourbaki7, Ch. VI, Exercises § 4, 10]).
$q\geq 2$ is finite for spherical and affine Coxeter systems (cf. [Reference Bourbaki7, Ch. VI, Exercises § 4, 10]).
Suppose (W, S) is of type ![]() $(4, 4, 4)$, that is,
$(4, 4, 4)$, that is, ![]() $\vert S \vert = 3$ and the order of st in W equals 4 for all
$\vert S \vert = 3$ and the order of st in W equals 4 for all ![]() $s\neq t\in S$. In [Reference Bischof5] we constructed uncountably many new examples of RGD systems of type
$s\neq t\in S$. In [Reference Bischof5] we constructed uncountably many new examples of RGD systems of type ![]() $(4, 4, 4)$ in which every root group has cardinality 2. As the criterion
$(4, 4, 4)$ in which every root group has cardinality 2. As the criterion ![]() $\vert S \vert \leq q_{\min}$ does not apply to such RGD systems, we first asked the question whether
$\vert S \vert \leq q_{\min}$ does not apply to such RGD systems, we first asked the question whether  $p_{(W, S)}\left( \frac{1}{2} \right) \lt \infty$ holds. It turns out that this is indeed the case (cf. Theorem A).
$p_{(W, S)}\left( \frac{1}{2} \right) \lt \infty$ holds. It turns out that this is indeed the case (cf. Theorem A).
Main results
Let (W, S) be a Coxeter system and denote by mst the order of st in W. The Coxeter system is called 2-spherical if ![]() $m_{st} \lt \infty$ for all
$m_{st} \lt \infty$ for all ![]() $s\neq t \in S$. The rank of (W, S) is given by the cardinality of S. Throughout this paper we assume that all Coxeter systems under consideration are of finite rank. We prove the following (cf. Theorem 5.3):
$s\neq t \in S$. The rank of (W, S) is given by the cardinality of S. Throughout this paper we assume that all Coxeter systems under consideration are of finite rank. We prove the following (cf. Theorem 5.3):
Theorem A. Let (W, S) be a 2-spherical Coxeter system of rank n. Then  $p_{(W, S)}\left( \frac{1}{n-1} \right) \lt \infty$.
$p_{(W, S)}\left( \frac{1}{n-1} \right) \lt \infty$.
Remark 1. After completion of this project, I was informed by Corentin Bodart that a more general version of Theorem A can be deduced from [Reference Arzhantseva and Lysenok2, Theorem 1] and we refer to Remark 3 at the end of the introduction for more details. Our methods of the proof are very different, and most of the results proved in the present paper are also used to prove Theorem C below. Our proofs are Coxeter group theoretic, while the proofs in [Reference Arzhantseva and Lysenok2] are for non-elementary word hyperbolic groups.
In view of the examples constructed in [Reference Bischof5], Theorem A produces many new examples of lattices in (locally compact) automorphism groups of buildings and in a product of two automorphism groups of buildings. Combining Theorem A with [Reference Rémy17, Théorème 1], we obtain that almost all RGD systems of 2-spherical type and rank 3 are twin building lattices:
Corollary B. Let (W, S) be a Coxeter system, and let ![]() $\mathcal{D} = (G, (U_{\alpha})_{\alpha \in \Phi})$ be an RGD system of type (W, S). Assume that the following are satisfied:
$\mathcal{D} = (G, (U_{\alpha})_{\alpha \in \Phi})$ be an RGD system of type (W, S). Assume that the following are satisfied:
• (W, S) is 2-spherical of rank 3 and W is infinite.
•
 $G = \langle U_{\alpha} \mid \alpha \in \Phi \rangle$,
$G = \langle U_{\alpha} \mid \alpha \in \Phi \rangle$,  $\vert Z(G) \vert \lt \infty$ and
$\vert Z(G) \vert \lt \infty$ and  $\vert U_{\alpha} \vert \lt \infty$ for all
$\vert U_{\alpha} \vert \lt \infty$ for all  $\alpha \in \Phi$.
$\alpha \in \Phi$.
Then, ![]() $\mathcal{D}$ is a twin building lattice.
$\mathcal{D}$ is a twin building lattice.
Corollary B. (Kac–Moody version)
Let (W, S) be a 2-spherical Coxeter system of rank 3 such that W is infinite, and let G be the Kac–Moody group (in the sense of [Reference Tits21]) of type (W, S). Then ![]() $\mathbf{G}(\mathbb{F}_q)$ is a twin building lattice, where
$\mathbf{G}(\mathbb{F}_q)$ is a twin building lattice, where ![]() $\mathbb{F}_q$ denotes the finite field with q elements.
$\mathbb{F}_q$ denotes the finite field with q elements.
Now the question is whether the finiteness still holds for some ![]() $q \lt n-1$. It turns out that in the class of Coxeter systems with
$q \lt n-1$. It turns out that in the class of Coxeter systems with ![]() $m_{st} \geq 3$ for all
$m_{st} \geq 3$ for all ![]() $s\neq t\in S$ this will not happen (cf. Theorem 5.5):
$s\neq t\in S$ this will not happen (cf. Theorem 5.5):
Theorem C. Let (W, S) be a Coxeter system of rank ![]() $n\geq 3$ such that
$n\geq 3$ such that ![]() $m_{st} \geq 3$ for all
$m_{st} \geq 3$ for all ![]() $s\neq t\in S$. Then,
$s\neq t\in S$. Then,  $p_{(W, S)}\left( \frac{1}{n-2} \right) = \infty$.
$p_{(W, S)}\left( \frac{1}{n-2} \right) = \infty$.
Suppose that the Coxeter diagram is 2-spherical, but the Coxeter diagram is not the complete graph. If the number of non-edges in the Coxeter diagram compared to the number of edges is large, then it is still possible that  $p_{(W, S)} \left( \frac{1}{n-2} \right) \lt \infty$ holds (cf. [Reference Terragni19]). We also remark that Theorem C can be used to exclude certain subdiagrams for twin building lattices, as parabolic subgroups of twin building lattices are again twin building lattices:
$p_{(W, S)} \left( \frac{1}{n-2} \right) \lt \infty$ holds (cf. [Reference Terragni19]). We also remark that Theorem C can be used to exclude certain subdiagrams for twin building lattices, as parabolic subgroups of twin building lattices are again twin building lattices:
Corollary D. Let (W, S) be a Coxeter system, let ![]() $\mathcal{D}$ be an RGD system of type (W, S) with finite root groups and let
$\mathcal{D}$ be an RGD system of type (W, S) with finite root groups and let ![]() $q_{\min} := \min\{\vert U_{\alpha} \vert \mid \alpha \in \Phi \}$. If
$q_{\min} := \min\{\vert U_{\alpha} \vert \mid \alpha \in \Phi \}$. If ![]() $\mathcal{D}$ is a twin building lattice, then there does not exist a subdiagram of (W, S) with at least
$\mathcal{D}$ is a twin building lattice, then there does not exist a subdiagram of (W, S) with at least ![]() $q_{\min} +2$ vertices, whose underlying Coxeter diagram is the complete graph.
$q_{\min} +2$ vertices, whose underlying Coxeter diagram is the complete graph.
Several remarks of our main results are in order.
Remark 2. The proofs of Theorem A and Theorem C make essential use of a result of Terragni [Reference Terragni20, Theorem A]. We recall this result in Subsection 5.1.
Remark 3. A more general version of Theorems A can be deduced from [Reference Arzhantseva and Lysenok2, Theorem 1]: Let (W, S) and ![]() $(W', S')$ be two Coxeter systems of rank
$(W', S')$ be two Coxeter systems of rank ![]() $n \geq 3$. Suppose that
$n \geq 3$. Suppose that ![]() $(W', S')$ is of universal type, i.e.
$(W', S')$ is of universal type, i.e. ![]() $m_{st} = \infty$ for all
$m_{st} = \infty$ for all ![]() $s\neq t\in S$. Note that W ʹ is word-hyperbolic (cf. [Reference Davis13, Corollary 12.6.3]) and non-elementary (in the sense of [Reference Arzhantseva and Lysenok2]; cf. [Reference Davis13, Theorem 8.6.1, 8.7.3]). Suppose that (W, S) is not of universal type. This means that
$s\neq t\in S$. Note that W ʹ is word-hyperbolic (cf. [Reference Davis13, Corollary 12.6.3]) and non-elementary (in the sense of [Reference Arzhantseva and Lysenok2]; cf. [Reference Davis13, Theorem 8.6.1, 8.7.3]). Suppose that (W, S) is not of universal type. This means that ![]() $m_{st} \lt \infty$ for some
$m_{st} \lt \infty$ for some ![]() $s\neq t \in S$. Let
$s\neq t \in S$. Let ![]() $\pi: W' \to W$ be a canonical homomorphism which induces a bijection between S ʹ and S. Then
$\pi: W' \to W$ be a canonical homomorphism which induces a bijection between S ʹ and S. Then ![]() $N := \ker(\pi)$ is a normal subgroup which is infinite. We now use the notation from [Reference Arzhantseva and Lysenok2]. One can show
$N := \ker(\pi)$ is a normal subgroup which is infinite. We now use the notation from [Reference Arzhantseva and Lysenok2]. One can show ![]() $\lambda(W', S') = n-1$, and by [Reference Arzhantseva and Lysenok2, Theorem 1] we have
$\lambda(W', S') = n-1$, and by [Reference Arzhantseva and Lysenok2, Theorem 1] we have ![]() $\lambda(W, S) \lt \lambda(W', S') = n-1$. We deduce from [Reference de la Harpe14, Chapter VI.C, Observation 50] that
$\lambda(W, S) \lt \lambda(W', S') = n-1$. We deduce from [Reference de la Harpe14, Chapter VI.C, Observation 50] that  $p_{(W, S)}\left( \frac{1}{n-1} \right) \lt \infty$. This implies that we can replace in Theorem A 2-spherical by non-universal.
$p_{(W, S)}\left( \frac{1}{n-1} \right) \lt \infty$. This implies that we can replace in Theorem A 2-spherical by non-universal.
Overview
In ![]() $\S$ 2, we fix notation and recall some basic results. In
$\S$ 2, we fix notation and recall some basic results. In ![]() $\S$ 2.2, we define two subsets Ci and Di of the Coxeter group W, which play a central role in this paper. In
$\S$ 2.2, we define two subsets Ci and Di of the Coxeter group W, which play a central role in this paper. In ![]() $\S$ 3, we recall the definition of reflection and combinatorial triangles and prove some results about them. In
$\S$ 3, we recall the definition of reflection and combinatorial triangles and prove some results about them. In ![]() $\S$ 4, we establish some (in-)equalities concerning the cardinalities
$\S$ 4, we establish some (in-)equalities concerning the cardinalities ![]() $\vert C_i \vert$ and
$\vert C_i \vert$ and ![]() $\vert D_i \vert$. In
$\vert D_i \vert$. In ![]() $\S$ 5, we recall a result due to Terragni and prove our main results.
$\S$ 5, we recall a result due to Terragni and prove our main results.
2. Preliminaries
This section is devoted to fixing notation. In ![]() $\S$ 2.1 which is based on [Reference Terragni20], we recall the notion of growth functions in finitely generated groups. In
$\S$ 2.1 which is based on [Reference Terragni20], we recall the notion of growth functions in finitely generated groups. In ![]() $\S$ 2.2 and
$\S$ 2.2 and ![]() $\S$ 2.3, we recall some basic definitions about Coxeter systems. Moreover, we introduce two sets Ci and Di which play a central role in this paper. In
$\S$ 2.3, we recall some basic definitions about Coxeter systems. Moreover, we introduce two sets Ci and Di which play a central role in this paper. In ![]() $\S$ 2.4, we recall some basic results about roots and walls in Coxeter systems.
$\S$ 2.4, we recall some basic results about roots and walls in Coxeter systems. ![]() $\S$ 2.2,
$\S$ 2.2, ![]() $\S$ 2.3 and
$\S$ 2.3 and ![]() $\S$ 2.4 are based on [Reference Abramenko and Brown1,
$\S$ 2.4 are based on [Reference Abramenko and Brown1, ![]() $\S$ 5].
$\S$ 5].
2.1. Growth of finitely generated groups
Let G be a finitely generated group, and let  $X = X^{-1} \subseteq G \backslash \{1\}$ be a finite, symmetric set of generators. The length of
$X = X^{-1} \subseteq G \backslash \{1\}$ be a finite, symmetric set of generators. The length of ![]() $g\in G$ with respect to X is the minimal n such that
$g\in G$ with respect to X is the minimal n such that ![]() $g = x_1 \cdots x_n$ with
$g = x_1 \cdots x_n$ with ![]() $x_i \in X$; the length function will be denoted by
$x_i \in X$; the length function will be denoted by ![]() $\ell_{(G, X)}: G \to \mathbb{N}$. For
$\ell_{(G, X)}: G \to \mathbb{N}$. For ![]() $n\in \mathbb{N}$, the sphere in
$n\in \mathbb{N}$, the sphere in ![]() $\mathrm{Cay}(G, X)$ centred around 1G with radius n will be denoted by
$\mathrm{Cay}(G, X)$ centred around 1G with radius n will be denoted by
 \begin{equation*} C_n^{(G, X)} := \left\{g\in G \mid \ell_{(G, X)}(g) = n \right\}. \end{equation*}
\begin{equation*} C_n^{(G, X)} := \left\{g\in G \mid \ell_{(G, X)}(g) = n \right\}. \end{equation*} The cardinalities are defined as  $c_n^{(G, X)} := \vert C_n^{(G, X)} \vert$. The growth function of (G, X) is given by
$c_n^{(G, X)} := \vert C_n^{(G, X)} \vert$. The growth function of (G, X) is given by
 \begin{equation*} p_{(G, X)}(t) := \sum_{n\geq 0} c_n^{(G, X)} t^n \in \mathbb{Z}[[t]]. \end{equation*}
\begin{equation*} p_{(G, X)}(t) := \sum_{n\geq 0} c_n^{(G, X)} t^n \in \mathbb{Z}[[t]]. \end{equation*}2.2. Coxeter systems
Let W be a group, and let ![]() $S \subseteq W$ be a generating set of elements of order 2. For
$S \subseteq W$ be a generating set of elements of order 2. For ![]() $s, t \in S$, we denote the order of st in W by mst. Then, the pair (W, S) is called Coxeter system if the group W admits the presentation
$s, t \in S$, we denote the order of st in W by mst. Then, the pair (W, S) is called Coxeter system if the group W admits the presentation
where there is one relation for each pair ![]() $s, t$ (possibly s = t) with
$s, t$ (possibly s = t) with ![]() $m_{st} \lt \infty$. Let (W, S) be a Coxeter system, and let
$m_{st} \lt \infty$. Let (W, S) be a Coxeter system, and let ![]() $\ell := \ell_{(W, S)}$ be the corresponding length function. The Coxeter diagram corresponding to (W, S) is the labelled graph
$\ell := \ell_{(W, S)}$ be the corresponding length function. The Coxeter diagram corresponding to (W, S) is the labelled graph ![]() $(S, E(S))$, where
$(S, E(S))$, where ![]() $E(S) = \{\{s, t \} \mid m_{st} \gt 2 \}$ and where each edge
$E(S) = \{\{s, t \} \mid m_{st} \gt 2 \}$ and where each edge ![]() $\{s,t\}$ is labelled by mst for all
$\{s,t\}$ is labelled by mst for all ![]() $s, t \in S$. The rank of the Coxeter system is the cardinality of the set S. Recall from the introduction that in this paper all Coxeter systems under consideration are assumed to be of finite rank.
$s, t \in S$. The rank of the Coxeter system is the cardinality of the set S. Recall from the introduction that in this paper all Coxeter systems under consideration are assumed to be of finite rank.
It is well-known that for each ![]() $J \subseteq S$, the pair
$J \subseteq S$, the pair ![]() $(\langle J \rangle, J)$ is a Coxeter system (cf. [Reference Bourbaki7, Ch. IV, §1 Theorem 2]). A subset
$(\langle J \rangle, J)$ is a Coxeter system (cf. [Reference Bourbaki7, Ch. IV, §1 Theorem 2]). A subset ![]() $J \subseteq S$ is called spherical if
$J \subseteq S$ is called spherical if ![]() $\langle J \rangle$ is finite. The Coxeter system is called 2-spherical if
$\langle J \rangle$ is finite. The Coxeter system is called 2-spherical if ![]() $\langle J \rangle$ is finite for all
$\langle J \rangle$ is finite for all ![]() $J \subseteq S$ containing at most 2 elements (i.e.
$J \subseteq S$ containing at most 2 elements (i.e. ![]() $m_{st} \lt \infty$ for all
$m_{st} \lt \infty$ for all ![]() $s, t \in S$). Given a spherical subset J of S, there exists a unique element of maximal length in
$s, t \in S$). Given a spherical subset J of S, there exists a unique element of maximal length in ![]() $\langle J \rangle$, which we denote by rJ (cf. [Reference Abramenko and Brown1, Corollary 2.19]).
$\langle J \rangle$, which we denote by rJ (cf. [Reference Abramenko and Brown1, Corollary 2.19]).
For ![]() $i \in \mathbb{N}$, we define
$i \in \mathbb{N}$, we define
•
 $C_i := C_i^{(W, S)} = \{w\in W \mid \ell(w) = i \}$ and
$C_i := C_i^{(W, S)} = \{w\in W \mid \ell(w) = i \}$ and  $c_i := \vert C_i \vert = c_i^{(W, S)}$;
$c_i := \vert C_i \vert = c_i^{(W, S)}$;•
 $D_i := \{w\in C_i \mid \exists! s\in S: \ell(ws) \lt \ell(w) \}$ and
$D_i := \{w\in C_i \mid \exists! s\in S: \ell(ws) \lt \ell(w) \}$ and  $d_i := \vert D_i \vert$.
$d_i := \vert D_i \vert$.
The set Ci consists of all elements ![]() $w\in W$ of length i. The set Di consists of all elements
$w\in W$ of length i. The set Di consists of all elements ![]() $w\in W$ of length i whose right descent set contains a single element of S.
$w\in W$ of length i whose right descent set contains a single element of S.
2.3. The chamber system  $\Sigma(W, S)$
$\Sigma(W, S)$
Let (W, S) be a Coxeter system. Defining ![]() $w \sim_s w'$ if and only if
$w \sim_s w'$ if and only if  $w^{-1}w' \in \langle s \rangle$, we obtain a chamber system (for the definition of a chamber system, see [Reference Abramenko and Brown1, Definition 5.21]) with chamber set W and equivalence relations
$w^{-1}w' \in \langle s \rangle$, we obtain a chamber system (for the definition of a chamber system, see [Reference Abramenko and Brown1, Definition 5.21]) with chamber set W and equivalence relations ![]() $\sim_s$ for
$\sim_s$ for ![]() $s\in S$, which we denote by
$s\in S$, which we denote by ![]() $\Sigma(W, S)$. We call two chambers
$\Sigma(W, S)$. We call two chambers ![]() $w, w'$ s-adjacent if
$w, w'$ s-adjacent if ![]() $w \sim_s w'$ and adjacent if they are s-adjacent for some
$w \sim_s w'$ and adjacent if they are s-adjacent for some ![]() $s\in S$. A gallery of length n from w 0 to wn is a sequence
$s\in S$. A gallery of length n from w 0 to wn is a sequence ![]() $(w_0, \ldots, w_n)$ of chambers, where wi and
$(w_0, \ldots, w_n)$ of chambers, where wi and ![]() $w_{i+1}$ are adjacent for each
$w_{i+1}$ are adjacent for each ![]() $0 \leq i \lt n$. A gallery
$0 \leq i \lt n$. A gallery ![]() $(w_0, \ldots, w_n)$ is called minimal if there exists no gallery from w 0 to wn of length k < n, and we denote the length of a minimal gallery from w 0 to wn by
$(w_0, \ldots, w_n)$ is called minimal if there exists no gallery from w 0 to wn of length k < n, and we denote the length of a minimal gallery from w 0 to wn by ![]() $\ell(w_0, w_n)$. For
$\ell(w_0, w_n)$. For ![]() $J \subseteq S$, we define the J-residue of a chamber
$J \subseteq S$, we define the J-residue of a chamber ![]() $c\in W$ to be the set
$c\in W$ to be the set ![]() $R_J(c) := c \langle J \rangle$. A residue R is a J-residue for some
$R_J(c) := c \langle J \rangle$. A residue R is a J-residue for some ![]() $J \subseteq S$; we call J the type of R, and the cardinality of J is called the rank of R. A residue is called spherical if its type is a spherical subset of S. Let R be a spherical J-residue. Two chambers
$J \subseteq S$; we call J the type of R, and the cardinality of J is called the rank of R. A residue is called spherical if its type is a spherical subset of S. Let R be a spherical J-residue. Two chambers ![]() $x, y \in R$ are called opposite in R if
$x, y \in R$ are called opposite in R if ![]() $x^{-1} y = r_J$. Two residues
$x^{-1} y = r_J$. Two residues ![]() $P, Q \subseteq R$ are called opposite in R if for each
$P, Q \subseteq R$ are called opposite in R if for each ![]() $p\in P$ there exists
$p\in P$ there exists ![]() $q\in Q$ such that
$q\in Q$ such that ![]() $p, q$ are opposite in R. A panel is a residue of rank 1. It is a fact that for every chamber
$p, q$ are opposite in R. A panel is a residue of rank 1. It is a fact that for every chamber ![]() $x\in W$ and every residue R, there exists a unique chamber
$x\in W$ and every residue R, there exists a unique chamber ![]() $z\in R$ such that
$z\in R$ such that ![]() $\ell(x, y) = \ell(x, z) + \ell(z, y)$ holds for each chamber
$\ell(x, y) = \ell(x, z) + \ell(z, y)$ holds for each chamber ![]() $y\in R$. The chamber z is called the projection or the gate of x onto R and is denoted by
$y\in R$. The chamber z is called the projection or the gate of x onto R and is denoted by ![]() $z = \operatorname{proj}_R x$.
$z = \operatorname{proj}_R x$.
A subset ![]() $\Sigma \subseteq W$ is called convex if for any two chambers
$\Sigma \subseteq W$ is called convex if for any two chambers ![]() $c, d \in \Sigma$ and any minimal gallery
$c, d \in \Sigma$ and any minimal gallery ![]() $(c_0 = c, \ldots, c_k = d)$, we have
$(c_0 = c, \ldots, c_k = d)$, we have ![]() $c_i \in \Sigma$ for all
$c_i \in \Sigma$ for all ![]() $0 \leq i \leq k$. Note that residues are convex by [Reference Abramenko and Brown1, Example 5.44(b)].
$0 \leq i \leq k$. Note that residues are convex by [Reference Abramenko and Brown1, Example 5.44(b)].
For two residues R and T, we define ![]() $\operatorname{proj}_T R := \{\operatorname{proj}_T r \mid r\in R \}$. By [Reference Abramenko and Brown1, Lemma 5.36(2)],
$\operatorname{proj}_T R := \{\operatorname{proj}_T r \mid r\in R \}$. By [Reference Abramenko and Brown1, Lemma 5.36(2)], ![]() $\operatorname{proj}_T R$ is a residue contained in T. The residues R and T are called parallel if
$\operatorname{proj}_T R$ is a residue contained in T. The residues R and T are called parallel if ![]() $\operatorname{proj}_T R = T$ and
$\operatorname{proj}_T R = T$ and ![]() $\operatorname{proj}_R T = R$.
$\operatorname{proj}_R T = R$.
2.4. Roots and walls
Let (W, S) be a Coxeter system. A reflection is an element of W that is conjugate to an element of S. For ![]() $s\in S$ we let
$s\in S$ we let ![]() $\alpha_s := \{w\in W \mid \ell(sw) \gt \ell(w) \}$ be the simple root corresponding to s. A root is a subset
$\alpha_s := \{w\in W \mid \ell(sw) \gt \ell(w) \}$ be the simple root corresponding to s. A root is a subset ![]() $\alpha \subseteq W$ such that
$\alpha \subseteq W$ such that ![]() $\alpha = v\alpha_s$ for some
$\alpha = v\alpha_s$ for some ![]() $v\in W$ and
$v\in W$ and ![]() $s\in S$. We denote the set of all roots by
$s\in S$. We denote the set of all roots by ![]() $\Phi := \Phi(W, S)$. The set
$\Phi := \Phi(W, S)$. The set ![]() $\Phi_+ := \{\alpha \in \Phi \mid 1_W \in \alpha \}$ is the set of all positive roots, and
$\Phi_+ := \{\alpha \in \Phi \mid 1_W \in \alpha \}$ is the set of all positive roots, and ![]() $\Phi_- := \{\alpha \in \Phi \mid 1_W \notin \alpha \}$ is the set of all negative roots. For each root
$\Phi_- := \{\alpha \in \Phi \mid 1_W \notin \alpha \}$ is the set of all negative roots. For each root ![]() $\alpha \in \Phi$, we denote the opposite root by
$\alpha \in \Phi$, we denote the opposite root by ![]() $-\alpha$ and we denote the unique reflection which interchanges these two roots by rα. For
$-\alpha$ and we denote the unique reflection which interchanges these two roots by rα. For ![]() $\alpha \in \Phi$, we denote by
$\alpha \in \Phi$, we denote by ![]() $\partial \alpha$ (respectively,
$\partial \alpha$ (respectively, ![]() $\partial^2 \alpha$) the set of all panels (respectively, spherical residues of rank 2) stabilized by rα. Furthermore, we define
$\partial^2 \alpha$) the set of all panels (respectively, spherical residues of rank 2) stabilized by rα. Furthermore, we define  $\mathcal{C}(\partial \alpha) := \bigcup_{P \in \partial \alpha} P$ and
$\mathcal{C}(\partial \alpha) := \bigcup_{P \in \partial \alpha} P$ and  $\mathcal{C}(\partial^2 \alpha) := \bigcup_{R \in \partial^2 \alpha} R$.
$\mathcal{C}(\partial^2 \alpha) := \bigcup_{R \in \partial^2 \alpha} R$.
The set ![]() $\partial \alpha$ is called the wall associated with α. Let
$\partial \alpha$ is called the wall associated with α. Let ![]() $G = (c_0, \ldots, c_k)$ be a gallery with
$G = (c_0, \ldots, c_k)$ be a gallery with ![]() $c_{i-1} \neq c_i$ for each
$c_{i-1} \neq c_i$ for each ![]() $1 \leq i \leq k$. We say that G crosses the wall
$1 \leq i \leq k$. We say that G crosses the wall ![]() $\partial \alpha$ if there exists
$\partial \alpha$ if there exists ![]() $1 \leq i \leq k$ such that
$1 \leq i \leq k$ such that ![]() $\{c_{i-1}, c_i \} \in \partial \alpha$. It is a basic fact that a minimal gallery crosses a wall at most once (cf. [Reference Abramenko and Brown1, Lemma 3.69]). Moreover, a gallery which crosses each wall at most once is already minimal.
$\{c_{i-1}, c_i \} \in \partial \alpha$. It is a basic fact that a minimal gallery crosses a wall at most once (cf. [Reference Abramenko and Brown1, Lemma 3.69]). Moreover, a gallery which crosses each wall at most once is already minimal.
A pair ![]() $\{\alpha, \beta \} \subseteq \Phi$ of roots is called prenilpotent, if
$\{\alpha, \beta \} \subseteq \Phi$ of roots is called prenilpotent, if ![]() $\alpha \cap \beta \neq \emptyset \neq (-\alpha) \cap (-\beta)$. For a prenilpotent pair
$\alpha \cap \beta \neq \emptyset \neq (-\alpha) \cap (-\beta)$. For a prenilpotent pair ![]() $\{\alpha, \beta \}$ of roots, we will write
$\{\alpha, \beta \}$ of roots, we will write ![]() $\left[\alpha,\beta\right]:=\{\gamma\in\Phi\mid\alpha\cap\beta\subseteq\gamma\;\text{and}\ (-\alpha)\cap(-\beta)\subseteq(-\gamma)\}$ and
$\left[\alpha,\beta\right]:=\{\gamma\in\Phi\mid\alpha\cap\beta\subseteq\gamma\;\text{and}\ (-\alpha)\cap(-\beta)\subseteq(-\gamma)\}$ and ![]() $(\alpha, \beta) := \left[ \alpha, \beta \right] \backslash \{\alpha, \beta \}$. We note that roots are convex (cf. [Reference Abramenko and Brown1, Lemma 3.44]).
$(\alpha, \beta) := \left[ \alpha, \beta \right] \backslash \{\alpha, \beta \}$. We note that roots are convex (cf. [Reference Abramenko and Brown1, Lemma 3.44]).
Let ![]() $(c_0, \ldots, c_k)$ and
$(c_0, \ldots, c_k)$ and ![]() $(d_0 = c_0, \ldots, d_k = c_k)$ be two minimal galleries from c 0 to ck, and let
$(d_0 = c_0, \ldots, d_k = c_k)$ be two minimal galleries from c 0 to ck, and let ![]() $\alpha \in \Phi$. Then,
$\alpha \in \Phi$. Then, ![]() $\partial \alpha$ is crossed by the minimal gallery
$\partial \alpha$ is crossed by the minimal gallery ![]() $(c_0, \ldots, c_k)$ if and only if it is crossed by the minimal gallery
$(c_0, \ldots, c_k)$ if and only if it is crossed by the minimal gallery ![]() $(d_0, \ldots, d_k)$.
$(d_0, \ldots, d_k)$.
Lemma 2.1. Let R be a spherical residue of ![]() $\Sigma(W, S)$ of rank 2, and let
$\Sigma(W, S)$ of rank 2, and let ![]() $\alpha \in \Phi$. Then, exactly one of the following holds:
$\alpha \in \Phi$. Then, exactly one of the following holds:
(a)
 $R \subseteq \alpha$;
$R \subseteq \alpha$;(b)
 $R \subseteq (-\alpha)$;
$R \subseteq (-\alpha)$;(c)
 $R \in \partial^2 \alpha$.
$R \in \partial^2 \alpha$.
Proof. It is clear that the three cases are exclusive. Suppose that ![]() $R \not\subseteq \alpha$ and
$R \not\subseteq \alpha$ and ![]() $R \not\subseteq (-\alpha)$. Then, there exist
$R \not\subseteq (-\alpha)$. Then, there exist ![]() $c \in R \cap (-\alpha)$ and
$c \in R \cap (-\alpha)$ and ![]() $d \in R \cap \alpha$. Let
$d \in R \cap \alpha$. Let ![]() $(c_0 = c, \ldots, c_k = d)$ be a minimal gallery. As residues are convex, we have
$(c_0 = c, \ldots, c_k = d)$ be a minimal gallery. As residues are convex, we have ![]() $c_i \in R$ for each
$c_i \in R$ for each ![]() $0 \leq i \leq k$. As
$0 \leq i \leq k$. As ![]() $c\in (-\alpha), d\in \alpha$, there exists
$c\in (-\alpha), d\in \alpha$, there exists ![]() $1 \leq i \leq k$, with
$1 \leq i \leq k$, with ![]() $c_{i-1} \in (-\alpha), c_i \in \alpha$. In particular,
$c_{i-1} \in (-\alpha), c_i \in \alpha$. In particular, ![]() $\{c_{i-1}, c_i \} \in \partial \alpha$ and hence
$\{c_{i-1}, c_i \} \in \partial \alpha$ and hence ![]() $R \in \partial^2 \alpha$.
$R \in \partial^2 \alpha$.
Lemma 2.2. Let ![]() $R, T$ be two spherical residues of
$R, T$ be two spherical residues of ![]() $\Sigma(W, S)$. Then, the following are equivalent:
$\Sigma(W, S)$. Then, the following are equivalent:
(i)
 $R, T$ are parallel;
$R, T$ are parallel;(ii) a reflection of
 $\Sigma(W, S)$ stabilizes R if and only if it stabilizes T;
$\Sigma(W, S)$ stabilizes R if and only if it stabilizes T;(iii) there exist two sequences
 $R_0 = R, \ldots, R_n = T$ and
$R_0 = R, \ldots, R_n = T$ and  $T_1, \ldots, T_n$ of residues of spherical type such that for each
$T_1, \ldots, T_n$ of residues of spherical type such that for each  $1 \leq i \leq n$, the rank of Ti is equal to
$1 \leq i \leq n$, the rank of Ti is equal to  $1+\mathrm{rank}(R)$, the residues
$1+\mathrm{rank}(R)$, the residues  $R_{i-1}, R_i$ are contained and opposite in Ti and moreover, we have
$R_{i-1}, R_i$ are contained and opposite in Ti and moreover, we have  $\operatorname{proj}_{T_i} R = R_{i-1}$ and
$\operatorname{proj}_{T_i} R = R_{i-1}$ and  $\operatorname{proj}_{T_i} T = R_i$.
$\operatorname{proj}_{T_i} T = R_i$.
Proof. This is [Reference Caprace and Mühlherr9, Proposition 2.7].
Lemma 2.3. Let ![]() $\alpha \in \Phi$ be a root, and let
$\alpha \in \Phi$ be a root, and let ![]() $x, y \in \alpha \cap \mathcal{C}(\partial \alpha)$. Then, there exists a minimal gallery
$x, y \in \alpha \cap \mathcal{C}(\partial \alpha)$. Then, there exists a minimal gallery ![]() $(c_0 = x, \ldots, c_k = y)$ such that
$(c_0 = x, \ldots, c_k = y)$ such that  $c_i \in \mathcal{C}(\partial^2 \alpha)$ for each
$c_i \in \mathcal{C}(\partial^2 \alpha)$ for each ![]() $0 \leq i \leq k$. Moreover, for each
$0 \leq i \leq k$. Moreover, for each ![]() $1 \leq i \leq k$, there exists
$1 \leq i \leq k$, there exists ![]() $L_i \in \partial^2 \alpha$ with
$L_i \in \partial^2 \alpha$ with ![]() $\{c_{i-1}, c_i \} \subseteq L_i$.
$\{c_{i-1}, c_i \} \subseteq L_i$.
Proof. This is a consequence of [Reference Caprace and Mühlherr8, Lemma 2.3] and its proof.
Lemma 2.4. Let ![]() $\alpha, \beta \in \Phi, \alpha \neq \pm \beta$ be two roots, and let
$\alpha, \beta \in \Phi, \alpha \neq \pm \beta$ be two roots, and let ![]() $R, T \in \partial^2 \alpha \cap \partial^2 \beta$.
$R, T \in \partial^2 \alpha \cap \partial^2 \beta$.
(a) The residues R and T are parallel.
(b) If
 $\vert \langle J \rangle \vert = \infty$ holds for all
$\vert \langle J \rangle \vert = \infty$ holds for all  $J \subseteq S$ containing three elements, then R = T.
$J \subseteq S$ containing three elements, then R = T.
Proof. As ![]() $R, T \in \partial^2 \alpha \cap \partial^2 \beta$, there exist panels
$R, T \in \partial^2 \alpha \cap \partial^2 \beta$, there exist panels ![]() $P_1, Q_1 \in \partial \alpha$ and
$P_1, Q_1 \in \partial \alpha$ and ![]() $P_2, Q_2 \in \partial \beta$ such that
$P_2, Q_2 \in \partial \beta$ such that ![]() $P_1, P_2 \subseteq R$ and
$P_1, P_2 \subseteq R$ and ![]() $Q_1, Q_2 \subseteq T$ (as in the proof of Lemma 2.1). By Lemma 2.2, the panels
$Q_1, Q_2 \subseteq T$ (as in the proof of Lemma 2.1). By Lemma 2.2, the panels ![]() $P_i, Q_i$ are parallel for both
$P_i, Q_i$ are parallel for both ![]() $i \in \{1, 2\}$. Now [Reference Devillers, Mühlherr and Van Maldeghem15, Lemma 17] yields that
$i \in \{1, 2\}$. Now [Reference Devillers, Mühlherr and Van Maldeghem15, Lemma 17] yields that ![]() $P_i, \operatorname{proj}_T P_i$ are parallel, and hence
$P_i, \operatorname{proj}_T P_i$ are parallel, and hence ![]() $\operatorname{proj}_T P_1 \in \partial \alpha, \operatorname{proj}_T P_2 \in \partial \beta$ by Lemma 2.2. As
$\operatorname{proj}_T P_1 \in \partial \alpha, \operatorname{proj}_T P_2 \in \partial \beta$ by Lemma 2.2. As ![]() $\alpha \neq \pm \beta$, we deduce
$\alpha \neq \pm \beta$, we deduce ![]() $\operatorname{proj}_T P_1 \neq \operatorname{proj}_T P_2$, and hence
$\operatorname{proj}_T P_1 \neq \operatorname{proj}_T P_2$, and hence ![]() $\operatorname{proj}_T R$ contains the two different panels
$\operatorname{proj}_T R$ contains the two different panels ![]() $\operatorname{proj}_T P_1$ and
$\operatorname{proj}_T P_1$ and ![]() $\operatorname{proj}_T P_2$. In particular,
$\operatorname{proj}_T P_2$. In particular, ![]() $\operatorname{proj}_T R$ is not a panel. Since
$\operatorname{proj}_T R$ is not a panel. Since ![]() $\operatorname{proj}_T R$ is a residue contained in T, we deduce
$\operatorname{proj}_T R$ is a residue contained in T, we deduce ![]() $\operatorname{proj}_T R = T$. Using similar arguments, we found that
$\operatorname{proj}_T R = T$. Using similar arguments, we found that ![]() $\operatorname{proj}_R T = R$ and
$\operatorname{proj}_R T = R$ and ![]() $R, T$ are parallel. This proves (a). Moreover, Lemma 2.2 yields R = T, as there are no spherical residues of rank 3 by assumption. This finishes the proof.
$R, T$ are parallel. This proves (a). Moreover, Lemma 2.2 yields R = T, as there are no spherical residues of rank 3 by assumption. This finishes the proof.
3. Reflection and combinatorial triangles in  $\Sigma(W, S)$
$\Sigma(W, S)$
Reflection triangles and combinatorial triangles were introduced in [Reference Caprace and Mühlherr8]. A reflection triangle is a set ![]() $\mathcal{R}$ of three reflections such that the order of tt ʹ is finite for all
$\mathcal{R}$ of three reflections such that the order of tt ʹ is finite for all ![]() $t, t' \in \mathcal{R}$, and
$t, t' \in \mathcal{R}$, and  $\bigcap_{t\in \mathcal{R}} \partial^2 \beta_t = \emptyset$, where βt is one of the two roots associated with the reflection t. Note that
$\bigcap_{t\in \mathcal{R}} \partial^2 \beta_t = \emptyset$, where βt is one of the two roots associated with the reflection t. Note that  $\partial^2 \beta_t = \partial^2 (-\beta_t)$. A set of three roots
$\partial^2 \beta_t = \partial^2 (-\beta_t)$. A set of three roots ![]() $\mathcal{T}$ is called a combinatorial triangle (or simply triangle) if the following holds:
$\mathcal{T}$ is called a combinatorial triangle (or simply triangle) if the following holds:
(CT1) The set
 $\{r_{\alpha} \mid \alpha \in \mathcal{T} \}$ is a reflection triangle.
$\{r_{\alpha} \mid \alpha \in \mathcal{T} \}$ is a reflection triangle.(CT2) For each
 $\alpha \in \mathcal{T}$, there exists
$\alpha \in \mathcal{T}$, there exists  $\sigma \in \partial^2 \beta \cap \partial^2 \gamma$ such that
$\sigma \in \partial^2 \beta \cap \partial^2 \gamma$ such that  $\sigma \subseteq \alpha$, where
$\sigma \subseteq \alpha$, where  $\{\beta, \gamma \} = \mathcal{T} \backslash \{\alpha \}$.
$\{\beta, \gamma \} = \mathcal{T} \backslash \{\alpha \}$.
Lemma 3.1. Suppose that (W, S) is 2-spherical and the Coxeter diagram is the complete graph. If ![]() $\mathcal{T}$ is a triangle, then
$\mathcal{T}$ is a triangle, then ![]() $(-\alpha, \beta) = \emptyset$ holds for all
$(-\alpha, \beta) = \emptyset$ holds for all ![]() $\alpha \neq \beta \in \mathcal{T}$.
$\alpha \neq \beta \in \mathcal{T}$.
Proof. This is [Reference Bischof4, Proposition 2.3].
Proposition 3.2. Assume that (W, S) is 2-spherical and the Coxeter diagram is the complete graph. Let R ≠ T be two residues of rank 2 such that ![]() $P := R \cap T$ is a panel. If
$P := R \cap T$ is a panel. If ![]() $\ell(1_W, \operatorname{proj}_R 1_W) \lt \ell(1_W, \operatorname{proj}_T 1_W)$, then
$\ell(1_W, \operatorname{proj}_R 1_W) \lt \ell(1_W, \operatorname{proj}_T 1_W)$, then ![]() $\operatorname{proj}_T 1_W = \operatorname{proj}_P 1_W$.
$\operatorname{proj}_T 1_W = \operatorname{proj}_P 1_W$.
Proof. We let ![]() $\alpha \in \Phi_+$ be the root with
$\alpha \in \Phi_+$ be the root with ![]() $P \in \partial \alpha$. Let
$P \in \partial \alpha$. Let ![]() $(c_0 = 1_W, \ldots, c_{k'} = \operatorname{proj}_P c_0)$ be a minimal gallery with
$(c_0 = 1_W, \ldots, c_{k'} = \operatorname{proj}_P c_0)$ be a minimal gallery with ![]() $c_k = \operatorname{proj}_R c_0$ for some
$c_k = \operatorname{proj}_R c_0$ for some ![]() $0 \leq k \leq k'$ and
$0 \leq k \leq k'$ and ![]() $c_k, \ldots, c_{k'} \in R$.
$c_k, \ldots, c_{k'} \in R$.
We assume that ![]() $\operatorname{proj}_T c_0 \neq \operatorname{proj}_P c_0$ holds. Then, we have
$\operatorname{proj}_T c_0 \neq \operatorname{proj}_P c_0$ holds. Then, we have ![]() $k' \gt \ell(1_W, \operatorname{proj}_T 1_W) \gt \ell(1_W, \operatorname{proj}_R 1_W) = k$. Let
$k' \gt \ell(1_W, \operatorname{proj}_T 1_W) \gt \ell(1_W, \operatorname{proj}_R 1_W) = k$. Let ![]() $(d_0 = 1_W, \ldots, d_{m'} = \operatorname{proj}_P d_0)$ be a minimal gallery with
$(d_0 = 1_W, \ldots, d_{m'} = \operatorname{proj}_P d_0)$ be a minimal gallery with ![]() $d_m = \operatorname{proj}_T c_0$ for some
$d_m = \operatorname{proj}_T c_0$ for some ![]() $0 \leq m \leq m'$ and
$0 \leq m \leq m'$ and ![]() $d_m, \ldots, d_{m'} \in T$. We let
$d_m, \ldots, d_{m'} \in T$. We let ![]() $\beta \in \Phi_+$ be the root with
$\beta \in \Phi_+$ be the root with ![]() $\{d_m, d_{m+1} \} \in \partial \beta$, and we let
$\{d_m, d_{m+1} \} \in \partial \beta$, and we let ![]() $\gamma \in \Phi_+$ be the root with
$\gamma \in \Phi_+$ be the root with ![]() $\{c_k, c_{k+1} \} \in \partial \gamma$. We will show that
$\{c_k, c_{k+1} \} \in \partial \gamma$. We will show that ![]() $\{\alpha, -\beta, -\gamma \}$ is a triangle. Thus, we first show that
$\{\alpha, -\beta, -\gamma \}$ is a triangle. Thus, we first show that ![]() $\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle. We have
$\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle. We have ![]() $T \in \partial^2 \alpha \cap \partial^2 \beta$, and, as a minimal gallery crosses a wall at most once, we deduce
$T \in \partial^2 \alpha \cap \partial^2 \beta$, and, as a minimal gallery crosses a wall at most once, we deduce ![]() $\alpha \neq \beta$. Note that the wall
$\alpha \neq \beta$. Note that the wall ![]() $\partial \beta$ is crossed by the minimal gallery
$\partial \beta$ is crossed by the minimal gallery ![]() $(c_0, \ldots, c_{k'})$. Since
$(c_0, \ldots, c_{k'})$. Since ![]() $\partial^2 \alpha \ni R \neq T \in \partial^2 \alpha \cap \partial^2 \beta$ and
$\partial^2 \alpha \ni R \neq T \in \partial^2 \alpha \cap \partial^2 \beta$ and ![]() $\alpha \neq \pm \beta$, Lemma 2.4(b) implies
$\alpha \neq \pm \beta$, Lemma 2.4(b) implies  $R \notin \partial^2 \beta$, and hence
$R \notin \partial^2 \beta$, and hence ![]() $\partial \beta$ is crossed by
$\partial \beta$ is crossed by ![]() $(c_0, \ldots, c_k)$. As
$(c_0, \ldots, c_k)$. As ![]() $k \lt k'$, we have
$k \lt k'$, we have ![]() $\operatorname{proj}_R 1_W \neq \operatorname{proj}_P 1_W$ and hence
$\operatorname{proj}_R 1_W \neq \operatorname{proj}_P 1_W$ and hence ![]() $\alpha \neq \gamma$. As
$\alpha \neq \gamma$. As ![]() $\alpha, \gamma \in \Phi_+$, we have
$\alpha, \gamma \in \Phi_+$, we have ![]() $\alpha \neq \pm \gamma$.
$\alpha \neq \pm \gamma$.
Assume that ![]() $o(r_{\beta} r_{\gamma}) = \infty$. We deduce
$o(r_{\beta} r_{\gamma}) = \infty$. We deduce ![]() $\beta \subseteq \gamma$. But
$\beta \subseteq \gamma$. But ![]() $\partial\gamma$ has to be crossed by the gallery
$\partial\gamma$ has to be crossed by the gallery ![]() $(d_0, \ldots, d_{m'})$. Since
$(d_0, \ldots, d_{m'})$. Since ![]() $\partial^2 \alpha \ni T \neq R \in \partial^2 \alpha \cap \partial^2 \gamma$ and
$\partial^2 \alpha \ni T \neq R \in \partial^2 \alpha \cap \partial^2 \gamma$ and ![]() $\alpha \neq \pm \gamma$, we have
$\alpha \neq \pm \gamma$, we have  $T \notin \partial \gamma^2$ by Lemma 2.4(b) as before. This implies that
$T \notin \partial \gamma^2$ by Lemma 2.4(b) as before. This implies that ![]() $(d_0, \ldots, d_m)$ crosses the wall
$(d_0, \ldots, d_m)$ crosses the wall ![]() $\partial \beta$ and hence
$\partial \beta$ and hence ![]() $\gamma \subseteq \beta$. This yields a contradiction, and we have
$\gamma \subseteq \beta$. This yields a contradiction, and we have ![]() $o(r_{\beta} r_{\gamma}) \lt \infty$.
$o(r_{\beta} r_{\gamma}) \lt \infty$.
As ![]() $R \in \partial^2 \alpha \cap \partial^2 \gamma$, Lemma 2.4(b) implies
$R \in \partial^2 \alpha \cap \partial^2 \gamma$, Lemma 2.4(b) implies  $\partial^2 \alpha \cap \partial^2 \gamma = \{R \}$. As
$\partial^2 \alpha \cap \partial^2 \gamma = \{R \}$. As  $R \notin \partial^2 \beta$, we deduce
$R \notin \partial^2 \beta$, we deduce ![]() $\partial^2 \alpha \cap \partial^2 \beta \cap \partial^2 \gamma = \emptyset$, and hence
$\partial^2 \alpha \cap \partial^2 \beta \cap \partial^2 \gamma = \emptyset$, and hence ![]() $\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle.
$\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle.
Now we have to verify (CT2). As ![]() $\partial^2 \gamma \not\ni T \in \partial^2 \alpha \cap \partial^2 \beta$ and
$\partial^2 \gamma \not\ni T \in \partial^2 \alpha \cap \partial^2 \beta$ and ![]() $P \subseteq T \cap (-\gamma)$, we have
$P \subseteq T \cap (-\gamma)$, we have ![]() $T \subseteq (-\gamma)$ by Lemma 2.1. As
$T \subseteq (-\gamma)$ by Lemma 2.1. As ![]() $\partial^2 \beta \not\ni R \in \partial^2 \alpha \cap \partial^2 \gamma$ and
$\partial^2 \beta \not\ni R \in \partial^2 \alpha \cap \partial^2 \gamma$ and ![]() $P \subseteq R \cap (-\beta)$, we have
$P \subseteq R \cap (-\beta)$, we have ![]() $R \subseteq (-\beta)$. Let
$R \subseteq (-\beta)$. Let ![]() $1 \leq i \leq k$ be such that
$1 \leq i \leq k$ be such that ![]() $\{c_{i-1}, c_i \} \in \partial \beta$. Note that
$\{c_{i-1}, c_i \} \in \partial \beta$. Note that ![]() $\{d_m, d_{m+1} \} \in \partial \beta, d_{m+1} \in (-\beta) \cap T \subseteq (-\gamma)$ and
$\{d_m, d_{m+1} \} \in \partial \beta, d_{m+1} \in (-\beta) \cap T \subseteq (-\gamma)$ and ![]() $c_i \in (-\beta) \cap \gamma$. By Lemma 2.3 there exists a minimal gallery
$c_i \in (-\beta) \cap \gamma$. By Lemma 2.3 there exists a minimal gallery ![]() $(e_0 = d_{m+1}, \ldots, e_z = c_i)$ such that
$(e_0 = d_{m+1}, \ldots, e_z = c_i)$ such that  $e_j \in \mathcal{C}(\partial^2 \beta)$. As
$e_j \in \mathcal{C}(\partial^2 \beta)$. As ![]() $d_{m+1} \in (-\gamma)$ and
$d_{m+1} \in (-\gamma)$ and ![]() $c_i \in \gamma$, there exists
$c_i \in \gamma$, there exists ![]() $1 \leq p \leq z$ such that
$1 \leq p \leq z$ such that ![]() $e_{p-1} \in (-\gamma)$ and
$e_{p-1} \in (-\gamma)$ and ![]() $e_p \in \gamma$. Again, by Lemma 2.3, there exists
$e_p \in \gamma$. Again, by Lemma 2.3, there exists ![]() $L \in \partial^2 \beta$ such that
$L \in \partial^2 \beta$ such that ![]() $\{e_{p-1}, e_p \} \subseteq L$, and hence
$\{e_{p-1}, e_p \} \subseteq L$, and hence ![]() $L \in \partial^2 \beta \cap \partial^2 \gamma$. As roots are convex and
$L \in \partial^2 \beta \cap \partial^2 \gamma$. As roots are convex and ![]() $e_0 = d_{m+1}, e_z = c_i \in \alpha$, we have
$e_0 = d_{m+1}, e_z = c_i \in \alpha$, we have ![]() $e_p \in L \cap \alpha$. As
$e_p \in L \cap \alpha$. As ![]() $\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle (and hence
$\{r_{\alpha}, r_{\beta}, r_{\gamma} \}$ is a reflection triangle (and hence  $L \notin \partial^2 \alpha$), we obtain
$L \notin \partial^2 \alpha$), we obtain ![]() $L \subseteq \alpha$ by Lemma 2.1. This implies that
$L \subseteq \alpha$ by Lemma 2.1. This implies that ![]() $\{\alpha, -\beta, -\gamma \}$ is a triangle, and hence
$\{\alpha, -\beta, -\gamma \}$ is a triangle, and hence ![]() $(\alpha, \gamma) = \emptyset$ holds by Lemma 3.1. In particular,
$(\alpha, \gamma) = \emptyset$ holds by Lemma 3.1. In particular, ![]() $k+1 = k'$ and
$k+1 = k'$ and ![]() $\ell(1_W, \operatorname{proj}_R 1_W) = \ell(1_W, \operatorname{proj}_P 1_W) -1 \geq \ell(1_W, \operatorname{proj}_T 1_W)$. This is a contradiction to the assumption, and we conclude
$\ell(1_W, \operatorname{proj}_R 1_W) = \ell(1_W, \operatorname{proj}_P 1_W) -1 \geq \ell(1_W, \operatorname{proj}_T 1_W)$. This is a contradiction to the assumption, and we conclude ![]() $\operatorname{proj}_T 1_W = \operatorname{proj}_P 1_W$.
$\operatorname{proj}_T 1_W = \operatorname{proj}_P 1_W$.
Corollary 3.3. Assume that (W, S) is 2-spherical and that the underlying Coxeter diagram is the complete graph. Suppose ![]() $w\in W$ and
$w\in W$ and ![]() $s\neq t \in S$ with
$s\neq t \in S$ with ![]() $\ell(ws) = \ell(w) +1 = \ell(wt)$ and suppose
$\ell(ws) = \ell(w) +1 = \ell(wt)$ and suppose ![]() $w' \in \langle s, t \rangle$ with
$w' \in \langle s, t \rangle$ with ![]() $\ell(w') \geq 2$. Then we have
$\ell(w') \geq 2$. Then we have ![]() $\ell(ww'r) = \ell(w) + \ell(w') +1$ for each
$\ell(ww'r) = \ell(w) + \ell(w') +1$ for each ![]() $r\in S \backslash \{s, t \}$.
$r\in S \backslash \{s, t \}$.
Proof. Suppose ![]() $r\in S \backslash \{s, t\}$, and assume that
$r\in S \backslash \{s, t\}$, and assume that ![]() $\ell(ww'r) = \ell(ww') -1$ holds for some
$\ell(ww'r) = \ell(ww') -1$ holds for some ![]() $w' \in \langle s, t \rangle$ with
$w' \in \langle s, t \rangle$ with ![]() $\ell(w') \geq 2$. Suppose
$\ell(w') \geq 2$. Suppose ![]() $w'$ starts with s, i.e.
$w'$ starts with s, i.e. ![]() $w' = sw^{\prime\prime}$ for some
$w' = sw^{\prime\prime}$ for some ![]() $w^{\prime\prime} \in \langle s, t \rangle$ with
$w^{\prime\prime} \in \langle s, t \rangle$ with ![]() $\ell(w^{\prime\prime}) = \ell(w') -1$. As
$\ell(w^{\prime\prime}) = \ell(w') -1$. As ![]() $\ell(ww'r) = \ell(ww') -1$, one easily sees that
$\ell(ww'r) = \ell(ww') -1$, one easily sees that ![]() $\ell(wstr) = \ell(wst) -1$ and
$\ell(wstr) = \ell(wst) -1$ and ![]() $\ell(wsr) = \ell(ws) -1$ hold, too. We define
$\ell(wsr) = \ell(ws) -1$ hold, too. We define  $R := R_{\{r, t\}}(ws), T := R_{\{s, t\}}(w)$ and
$R := R_{\{r, t\}}(ws), T := R_{\{s, t\}}(w)$ and ![]() $P := R \cap T = \mathcal{P}_t(ws)$. Clearly,
$P := R \cap T = \mathcal{P}_t(ws)$. Clearly, ![]() $\operatorname{proj}_T 1_W \neq \operatorname{proj}_P 1_W$. As
$\operatorname{proj}_T 1_W \neq \operatorname{proj}_P 1_W$. As ![]() $m_{rt} \geq 3$, we deduce
$m_{rt} \geq 3$, we deduce ![]() $\ell(1_W, \operatorname{proj}_R 1_W) \lt \ell(1_W, \operatorname{proj}_T 1_W)$ and Proposition 3.2 yields a contradiction.
$\ell(1_W, \operatorname{proj}_R 1_W) \lt \ell(1_W, \operatorname{proj}_T 1_W)$ and Proposition 3.2 yields a contradiction.
Lemma 3.4. Assume that (W, S) is 2-spherical and that ![]() $m_{st} \geq 4$ holds for all
$m_{st} \geq 4$ holds for all ![]() $s\neq t \in S$. Suppose
$s\neq t \in S$. Suppose ![]() $w \in W$ and
$w \in W$ and ![]() $s\neq t \in S$ with
$s\neq t \in S$ with ![]() $\ell(ws) = \ell(w) +1 = \ell(wt)$. Then we have
$\ell(ws) = \ell(w) +1 = \ell(wt)$. Then we have ![]() $\ell(w) +2 \in \{\ell(wsr), \ell(wtr) \}$ for all
$\ell(w) +2 \in \{\ell(wsr), \ell(wtr) \}$ for all ![]() $r\in S \backslash \{s, t\}$.
$r\in S \backslash \{s, t\}$.
Proof. Assume that ![]() $\ell(wsr) = \ell(w) = \ell(wtr)$. Then,
$\ell(wsr) = \ell(w) = \ell(wtr)$. Then, ![]() $\ell(wr) = \ell(w)-1$ and
$\ell(wr) = \ell(w)-1$ and ![]() $\ell(wrs) = \ell(w) -2 = \ell(wrt)$. Let R be the
$\ell(wrs) = \ell(w) -2 = \ell(wrt)$. Let R be the ![]() $\{r, s \}$-residue containing w. As
$\{r, s \}$-residue containing w. As ![]() $m_{rs} \geq 4$, we deduce
$m_{rs} \geq 4$, we deduce ![]() $\ell(wrsr) = \ell(wrs) -1$. Let
$\ell(wrsr) = \ell(wrs) -1$. Let ![]() $w' \in \langle s, t \rangle$ be such that
$w' \in \langle s, t \rangle$ be such that ![]() $wr = (\operatorname{proj}_R 1_W) w'$. Then,
$wr = (\operatorname{proj}_R 1_W) w'$. Then, ![]() $\ell(w') \geq 2$ and the previous corollary implies
$\ell(w') \geq 2$ and the previous corollary implies ![]() $\ell(wrt) = \ell(wr) +1$, which is a contradiction. This finishes the proof.
$\ell(wrt) = \ell(wr) +1$, which is a contradiction. This finishes the proof.
Remark 3.5. Note that Lemma 3.4 is false without the assumption ![]() $m_{st} \geq 4$. To see this, one can consider the Coxeter system of type
$m_{st} \geq 4$. To see this, one can consider the Coxeter system of type ![]() $\tilde{A}_2$.
$\tilde{A}_2$.
4. Some (in-)equalities
To show the two main results (Theorem 5.3 and 5.5), we will apply the ratio test. In order to do so, we need a few inequalities, which we establish in this and the next section. We recall that for ![]() $i\in \mathbb{N}$ we have
$i\in \mathbb{N}$ we have
•
 $C_i := \{w\in W \mid \ell(w) = i \}$ and
$C_i := \{w\in W \mid \ell(w) = i \}$ and  $c_i := \vert C_i \vert$;
$c_i := \vert C_i \vert$;•
 $D_i := \{w\in C_i \mid \exists! s\in S: \ell(ws) \lt \ell(w) \}$ and
$D_i := \{w\in C_i \mid \exists! s\in S: \ell(ws) \lt \ell(w) \}$ and  $d_i := \vert D_i \vert$;
$d_i := \vert D_i \vert$;
Lemma 4.1. Suppose that the Coxeter diagram of (W, S) is the complete graph. Then, for each ![]() $w\in W \backslash \{1_W\}$, there is either a unique element
$w\in W \backslash \{1_W\}$, there is either a unique element ![]() $s_w \in S$ with
$s_w \in S$ with ![]() $\ell(w s_w) = \ell(w) -1$, or else there are exactly two elements
$\ell(w s_w) = \ell(w) -1$, or else there are exactly two elements ![]() $s_w \neq t_w \in S$ with
$s_w \neq t_w \in S$ with ![]() $\ell(w s_w) = \ell(w) -1 = \ell(w t_w)$.
$\ell(w s_w) = \ell(w) -1 = \ell(w t_w)$.
Proof. Let ![]() $J \subseteq S$ with
$J \subseteq S$ with ![]() $\ell(wj) \lt \ell(w)$ for each
$\ell(wj) \lt \ell(w)$ for each ![]() $j \in J$. Then [Reference Abramenko and Brown1, Corollary 2.18] implies that J is spherical. As the underlying Coxeter diagram is the complete graph, it follows that each subset of S containing at least three elements is non-spherical. This finishes the proof.
$j \in J$. Then [Reference Abramenko and Brown1, Corollary 2.18] implies that J is spherical. As the underlying Coxeter diagram is the complete graph, it follows that each subset of S containing at least three elements is non-spherical. This finishes the proof.
Convention 4.2.
In this section, we assume that (W, S) is of rank ![]() $n \geq 3$ and that there exists
$n \geq 3$ and that there exists ![]() $m\geq 3$ such that
$m\geq 3$ such that ![]() $m_{st} = m$ holds for all
$m_{st} = m$ holds for all ![]() $s\neq t \in S$. Moreover, we let i > m.
$s\neq t \in S$. Moreover, we let i > m.
Lemma 4.3.  $c_i - d_i = \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} c_{i-m} + (n-2) d_{i-m}$.
$c_i - d_i = \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} c_{i-m} + (n-2) d_{i-m}$.
Proof. Let ![]() $v \in C_i \backslash D_i$ be an element. By Lemma 4.1, there exist exactly two elements
$v \in C_i \backslash D_i$ be an element. By Lemma 4.1, there exist exactly two elements ![]() $s\neq t \in S$ with
$s\neq t \in S$ with ![]() $\ell(vs) = \ell(v) -1 = \ell(vt)$. We define
$\ell(vs) = \ell(v) -1 = \ell(vt)$. We define  $R_v := R_{\{s, t\}}(v)$. Then, we consider the mapping
$R_v := R_{\{s, t\}}(v)$. Then, we consider the mapping
 \begin{equation*} f: C_i \backslash D_i \to C_{i-m}, v \mapsto \operatorname{proj}_{R_v} 1_W \end{equation*}
\begin{equation*} f: C_i \backslash D_i \to C_{i-m}, v \mapsto \operatorname{proj}_{R_v} 1_W \end{equation*} Note that ![]() $C_{i-m} = D_{i-m} \cup C_{i-m} \backslash D_{i-m}$. If
$C_{i-m} = D_{i-m} \cup C_{i-m} \backslash D_{i-m}$. If ![]() $w\in C_{i-m} \backslash D_{i-m}$, Lemma 4.1 implies that there are exactly two elements in S, say
$w\in C_{i-m} \backslash D_{i-m}$, Lemma 4.1 implies that there are exactly two elements in S, say ![]() $s_w \neq t_w \in S$, which decreases the length of w (as i > m). Any other element
$s_w \neq t_w \in S$, which decreases the length of w (as i > m). Any other element ![]() $r\in S \backslash \{s_w, t_w \}$ increases the length of w. For n > 3 and
$r\in S \backslash \{s_w, t_w \}$ increases the length of w. For n > 3 and ![]() $r_1 \neq r_2 \in S \backslash \{s_w, t_w\}$, we have
$r_1 \neq r_2 \in S \backslash \{s_w, t_w\}$, we have  $f(wr_{\{r_1, r_2\}}) = w$. For n = 3, we have
$f(wr_{\{r_1, r_2\}}) = w$. For n = 3, we have  $f^{-1}(w) = \emptyset$. In both cases, w has
$f^{-1}(w) = \emptyset$. In both cases, w has  $\begin{pmatrix}
n-2 \\ 2
\end{pmatrix}$ many preimages. If
$\begin{pmatrix}
n-2 \\ 2
\end{pmatrix}$ many preimages. If ![]() $w \in D_{i-m}$ is, there exists a unique
$w \in D_{i-m}$ is, there exists a unique ![]() $s_w \in S$ which decreases the length of w and (similarly as before) w has
$s_w \in S$ which decreases the length of w and (similarly as before) w has  $\begin{pmatrix}
n-1 \\ 2
\end{pmatrix}$ many preimages. Note that
$\begin{pmatrix}
n-1 \\ 2
\end{pmatrix}$ many preimages. Note that  $\begin{pmatrix}
n-1 \\ 2
\end{pmatrix} - \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} = n-2$. We conclude
$\begin{pmatrix}
n-1 \\ 2
\end{pmatrix} - \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} = n-2$. We conclude
 \begin{align*}
c_i - d_i = \vert C_i \backslash D_i \vert &= \sum_{w\in C_{i-m}} \vert f^{-1}(w) \vert \\
&= \sum_{w\in C_{i-m} \backslash D_{i-m}} \vert f^{-1}(w) \vert + \sum_{w\in D_{i-m}} \vert f^{-1}(w) \vert \\
&= \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} \left( c_{i-m} - d_{i-m} \right) + \begin{pmatrix}
n-1 \\ 2
\end{pmatrix} d_{i-m} \\
&= \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} c_{i-m} + (n-2) d_{i-m}.
\end{align*}
\begin{align*}
c_i - d_i = \vert C_i \backslash D_i \vert &= \sum_{w\in C_{i-m}} \vert f^{-1}(w) \vert \\
&= \sum_{w\in C_{i-m} \backslash D_{i-m}} \vert f^{-1}(w) \vert + \sum_{w\in D_{i-m}} \vert f^{-1}(w) \vert \\
&= \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} \left( c_{i-m} - d_{i-m} \right) + \begin{pmatrix}
n-1 \\ 2
\end{pmatrix} d_{i-m} \\
&= \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} c_{i-m} + (n-2) d_{i-m}.
\end{align*}Lemma 4.4. ![]() $2c_{i+1} - d_{i+1} = (n-2) c_i + d_i$.
$2c_{i+1} - d_{i+1} = (n-2) c_i + d_i$.
Proof. We put ![]() $M_i := \{(w, s) \in C_i \times S \mid ws \in C_{i+1} \}$. We prove the claim by showing that both sides of the equation are equal to
$M_i := \{(w, s) \in C_i \times S \mid ws \in C_{i+1} \}$. We prove the claim by showing that both sides of the equation are equal to ![]() $\vert M_i \vert$.
$\vert M_i \vert$.
(a)
 $2c_{i+1} - d_{i+1} = \vert M_i \vert$: We consider the mapping
$2c_{i+1} - d_{i+1} = \vert M_i \vert$: We consider the mapping
 \begin{equation*} \pi: M_i \to C_{i+1}, (w, s) \mapsto ws. \end{equation*}
\begin{equation*} \pi: M_i \to C_{i+1}, (w, s) \mapsto ws. \end{equation*}Clearly, π is surjective. We define
 \begin{align*}
&C_{i+1}^1 := \{w\in C_{i+1} \mid \vert \pi^{-1}(w) \vert = 1 \} &&\text{and} &&C_{i+1}^{ \gt 1} := \{w\in C_{i+1} \mid \vert \pi^{-1}(w) \vert \gt 1 \}.
\end{align*}
\begin{align*}
&C_{i+1}^1 := \{w\in C_{i+1} \mid \vert \pi^{-1}(w) \vert = 1 \} &&\text{and} &&C_{i+1}^{ \gt 1} := \{w\in C_{i+1} \mid \vert \pi^{-1}(w) \vert \gt 1 \}.
\end{align*}We show that
 $C_{i+1}^{ \gt 1} = C_{i+1} \backslash D_{i+1}$. Let
$C_{i+1}^{ \gt 1} = C_{i+1} \backslash D_{i+1}$. Let  $\bar{w} \in C_{i+1}^{ \gt 1}$ be an element. Then, there exist
$\bar{w} \in C_{i+1}^{ \gt 1}$ be an element. Then, there exist  $(w, s) \neq (w', s') \in \pi^{-1}(\bar{w})$. It follows that
$(w, s) \neq (w', s') \in \pi^{-1}(\bar{w})$. It follows that  $s\neq s'$, and hence
$s\neq s'$, and hence  $\bar{w} \in C_{i+1} \backslash D_{i+1}$. Now, let
$\bar{w} \in C_{i+1} \backslash D_{i+1}$. Now, let  $w\in C_{i+1} \backslash D_{i+1}$. By Lemma 4.1, there exist exactly two elements
$w\in C_{i+1} \backslash D_{i+1}$. By Lemma 4.1, there exist exactly two elements  $s_w \neq t_w \in S$, which decreases the length of w. This implies
$s_w \neq t_w \in S$, which decreases the length of w. This implies  $(ws_w, s_w) \neq (wt_w, t_w) \in \pi^{-1}(w)$. As
$(ws_w, s_w) \neq (wt_w, t_w) \in \pi^{-1}(w)$. As  $\vert \langle J \rangle \vert = \infty$ for all
$\vert \langle J \rangle \vert = \infty$ for all  $J \subseteq S$ containing three elements, we deduce for every
$J \subseteq S$ containing three elements, we deduce for every  $1 \neq w\in W$ that
$1 \neq w\in W$ that
 \begin{equation*} \vert \pi^{-1}(w) \vert \in \{1, 2 \}. \end{equation*}
\begin{equation*} \vert \pi^{-1}(w) \vert \in \{1, 2 \}. \end{equation*}We infer
 $C_{i+1}^1 = C_{i+1} \backslash C_{i+1}^{ \gt 1} = C_{i+1} \backslash \left( C_{i+1} \backslash D_{i+1} \right) = D_{i+1}$ and compute
$C_{i+1}^1 = C_{i+1} \backslash C_{i+1}^{ \gt 1} = C_{i+1} \backslash \left( C_{i+1} \backslash D_{i+1} \right) = D_{i+1}$ and compute
 \begin{align*}
\vert M_i \vert = \sum_{w\in C_{i+1}} \vert \pi^{-1}(w) \vert &= \sum_{w\in D_{i+1}} \vert \pi^{-1}(w) \vert + \sum_{w\in C_{i+1} \backslash D_{i+1}} \vert \pi^{-1}(w) \vert \\
&= d_{i+1} + 2(c_{i+1} - d_{i+1}) \\
&= 2c_{i+1} - d_{i+1}.
\end{align*}
\begin{align*}
\vert M_i \vert = \sum_{w\in C_{i+1}} \vert \pi^{-1}(w) \vert &= \sum_{w\in D_{i+1}} \vert \pi^{-1}(w) \vert + \sum_{w\in C_{i+1} \backslash D_{i+1}} \vert \pi^{-1}(w) \vert \\
&= d_{i+1} + 2(c_{i+1} - d_{i+1}) \\
&= 2c_{i+1} - d_{i+1}.
\end{align*}(b)
 $(n-2) c_i + d_i = \vert M_i \vert$: For a subset
$(n-2) c_i + d_i = \vert M_i \vert$: For a subset  $T \subseteq C_i$, we define
$T \subseteq C_i$, we define
 \begin{align*}
M_{i, T} &:= \{(w, s) \in M_i \mid w \in T \}.
\end{align*}
\begin{align*}
M_{i, T} &:= \{(w, s) \in M_i \mid w \in T \}.
\end{align*}For
 $w\in D_i$ there are exactly n − 1 elements which increase the length of w. Thus, we have
$w\in D_i$ there are exactly n − 1 elements which increase the length of w. Thus, we have  $\vert M_{i, D_i} \vert = (n-1)d_i$. For
$\vert M_{i, D_i} \vert = (n-1)d_i$. For  $w\in C_i \backslash D_i$, there are exactly n − 2 elements in S, which increases the length of w (cf. Lemma 4.1). Thus, we have
$w\in C_i \backslash D_i$, there are exactly n − 2 elements in S, which increases the length of w (cf. Lemma 4.1). Thus, we have  $\vert M_{i, C_i \backslash D_i} \vert = (n-2)(c_i - d_i)$. We conclude
$\vert M_{i, C_i \backslash D_i} \vert = (n-2)(c_i - d_i)$. We conclude
 \begin{equation*}
\vert M_i \vert = \vert M_{i, C_i \backslash D_i} \vert + \vert M_{i, D_i} \vert = (n-2) (c_i - d_i) + (n-1)d_i = (n-2) c_i + d_i.
\end{equation*}
\begin{equation*}
\vert M_i \vert = \vert M_{i, C_i \backslash D_i} \vert + \vert M_{i, D_i} \vert = (n-2) (c_i - d_i) + (n-1)d_i = (n-2) c_i + d_i.
\end{equation*}
Lemma 4.5. ![]() $c_{i+1} \leq (n-1) c_i - (n-2)d_{i-m+1} \leq (n-1) c_i$.
$c_{i+1} \leq (n-1) c_i - (n-2)d_{i-m+1} \leq (n-1) c_i$.
Proof. The last inequality is obvious. Using Lemma 4.3 and 4.4, we deduce the following:
Lemma 4.6. Suppose m > 3. Then, the following holds:
(a)
 $(n-2) c_i \leq c_{i+1}$;
$(n-2) c_i \leq c_{i+1}$;(b)
 $(n-2) d_i \leq d_{i+1}$;
$(n-2) d_i \leq d_{i+1}$;
Proof. We define ![]() $N_i := \{(w, s) \in C_i \times S \mid ws \in D_{i+1} \}$. Then,
$N_i := \{(w, s) \in C_i \times S \mid ws \in D_{i+1} \}$. Then, ![]() $N_i \to D_{i+1}, (w, s) \mapsto ws$ is a bijection, and hence
$N_i \to D_{i+1}, (w, s) \mapsto ws$ is a bijection, and hence ![]() $\vert N_i \vert = d_{i+1}$. As in the proof of Lemma 4.4, we define for a subset
$\vert N_i \vert = d_{i+1}$. As in the proof of Lemma 4.4, we define for a subset ![]() $T \subseteq C_i$:
$T \subseteq C_i$:
We see that  $c_{i+1} \geq d_{i+1} = \vert N_i \vert = \vert N_{i, D_i} \vert + \vert N_{i, C_i \backslash D_i} \vert$. Let
$c_{i+1} \geq d_{i+1} = \vert N_i \vert = \vert N_{i, D_i} \vert + \vert N_{i, C_i \backslash D_i} \vert$. Let ![]() $w\in C_i$. We now count pairs
$w\in C_i$. We now count pairs ![]() $(w, s) \in N_i$. We distinguish the following two cases:
$(w, s) \in N_i$. We distinguish the following two cases:
(i)
 $w\in D_i$: Let
$w\in D_i$: Let  $s_w \in S$ be the unique element with
$s_w \in S$ be the unique element with  $\ell(ws_w) \lt \ell(w)$. Let
$\ell(ws_w) \lt \ell(w)$. Let  $t\in S \backslash \{s_w \}$. Then,
$t\in S \backslash \{s_w \}$. Then,  $wt \in C_{i+1}$. Suppose
$wt \in C_{i+1}$. Suppose  $wt \notin D_{i+1}$. Then, there exists
$wt \notin D_{i+1}$. Then, there exists  $t\neq r \in S$ with
$t\neq r \in S$ with  $\ell(wtr) \lt \ell(wt)$. This implies
$\ell(wtr) \lt \ell(wt)$. This implies  $\ell(wr) \lt \ell(w)$, and the uniqueness of sw yields
$\ell(wr) \lt \ell(w)$, and the uniqueness of sw yields  $r = s_w$. Now, let
$r = s_w$. Now, let  $r \in S \backslash \{s_w, t\}$. Then
$r \in S \backslash \{s_w, t\}$. Then  $wr \in C_{i+1}$. Again, if
$wr \in C_{i+1}$. Again, if  $wr \notin D_{i+1}$, then sw would decrease the length of wr. But this is a contradiction to Lemma 3.4. This implies
$wr \notin D_{i+1}$, then sw would decrease the length of wr. But this is a contradiction to Lemma 3.4. This implies  $(w, r) \in N_{i, D_i}$ for all
$(w, r) \in N_{i, D_i}$ for all  $r\in S \backslash \{s_w, t\}$. This shows (b).
$r\in S \backslash \{s_w, t\}$. This shows (b).(ii)
 $w\in C_i \backslash D_i$: Let
$w\in C_i \backslash D_i$: Let  $s_w \neq t_w \in S$ be the two elements with
$s_w \neq t_w \in S$ be the two elements with  $\ell(w s_w) = \ell(w t_w) \lt \ell(w)$. Now let
$\ell(w s_w) = \ell(w t_w) \lt \ell(w)$. Now let  $r\in S \backslash \{s_w, t_w \}$. Then,
$r\in S \backslash \{s_w, t_w \}$. Then,  $wr \in C_{i+1}$. We assume by contradiction that
$wr \in C_{i+1}$. We assume by contradiction that  $wr \notin D_{i+1}$. Then, there would exist
$wr \notin D_{i+1}$. Then, there would exist  $u \in S \backslash \{r \}$ with
$u \in S \backslash \{r \}$ with  $\ell(wr u) = \ell(w)$, and hence
$\ell(wr u) = \ell(w)$, and hence  $\ell(wu) \lt \ell(w)$. As sw and tw are the only two elements in S with the property that they decrease the length of w, we obtain
$\ell(wu) \lt \ell(w)$. As sw and tw are the only two elements in S with the property that they decrease the length of w, we obtain  $u \in \{s_w, t_w \}$. But then, we obtain a contradiction to Corollary 3.3. We conclude
$u \in \{s_w, t_w \}$. But then, we obtain a contradiction to Corollary 3.3. We conclude  $(w, r) \in N_{i, C_i \backslash D_i}$.
$(w, r) \in N_{i, C_i \backslash D_i}$.
We infer  $c_{i+1} \geq \vert N_{i, D_i} \vert + \vert N_{i, C_i \backslash D_i} \vert \geq (n-2) d_i + (n-2) (c_i - d_i) = (n-2) c_i$.
$c_{i+1} \geq \vert N_{i, D_i} \vert + \vert N_{i, C_i \backslash D_i} \vert \geq (n-2) d_i + (n-2) (c_i - d_i) = (n-2) c_i$.
5. Main results
In this section, we prove our main results. In ![]() $\S$ 5.1, we recall a reduction result due to Terragni. In
$\S$ 5.1, we recall a reduction result due to Terragni. In ![]() $\S$ 5.2, we use the reduction result to prove convergence of
$\S$ 5.2, we use the reduction result to prove convergence of  $p_{(W, S)}\left(\frac{1}{n-1}\right)$, where (W, S) is 2-spherical of rank
$p_{(W, S)}\left(\frac{1}{n-1}\right)$, where (W, S) is 2-spherical of rank ![]() $n \geq 3$. In
$n \geq 3$. In ![]() $\S$ 5.3, we use the reduction result to prove divergence of
$\S$ 5.3, we use the reduction result to prove divergence of  $p_{(W, S)}\left( \frac{1}{n-2} \right)$, where (W, S) is of rank
$p_{(W, S)}\left( \frac{1}{n-2} \right)$, where (W, S) is of rank ![]() $n \geq 4$ and the underlying Coxeter diagram is the complete graph.
$n \geq 4$ and the underlying Coxeter diagram is the complete graph.
5.1. Reduction step
Let (W, S) and ![]() $(W', S')$ be two Coxeter systems. Following [Reference Terragni20], we define
$(W', S')$ be two Coxeter systems. Following [Reference Terragni20], we define ![]() $(W, S) \preceq (W', S')$ if there exists an injective map
$(W, S) \preceq (W', S')$ if there exists an injective map ![]() $\varphi: S \to S'$ satisfying
$\varphi: S \to S'$ satisfying  $m_{st} \leq m'_{\varphi(s)\varphi(t)}$ for all
$m_{st} \leq m'_{\varphi(s)\varphi(t)}$ for all ![]() $s, t\in S$.
$s, t\in S$.
Theorem 5.1. Let (W, S) and ![]() $(W', S')$ be two Coxeter systems, and let
$(W', S')$ be two Coxeter systems, and let  $c_n := c_n^{(W, S)}$ and
$c_n := c_n^{(W, S)}$ and  $c_n' := c_n^{(W', S')}$. If
$c_n' := c_n^{(W', S')}$. If ![]() $(W, S) \preceq (W', S')$, then
$(W, S) \preceq (W', S')$, then ![]() $c_n \leq c_n'$.
$c_n \leq c_n'$.
Proof. This is [Reference Terragni20, Theorem A].
5.2. Convergence
Lemma 5.2. Let (W, S) be of rank ![]() $n \geq 3$, and assume that there exists
$n \geq 3$, and assume that there exists ![]() $m \geq 4$ such that
$m \geq 4$ such that ![]() $m_{st} = m$ holds for all
$m_{st} = m$ holds for all ![]() $s\neq t \in S$. Then, there exists
$s\neq t \in S$. Then, there exists ![]() $k \in \mathbb{R}$ such that
$k \in \mathbb{R}$ such that  $\frac{d_i}{c_i} \geq k \gt 0$ holds for all i > m.
$\frac{d_i}{c_i} \geq k \gt 0$ holds for all i > m.
Proof. Using Lemma 4.3 and 4.6, we compute
 \begin{align*}
1 = \frac{c_i -d_i +d_i}{c_i} &= \frac{1}{c_i}\left( \begin{pmatrix}
n-2 \\ 2
\end{pmatrix}c_{i-m} + (n-2)d_{i-m} + d_i \right) \\
&\leq \frac{1}{c_i}\left( \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} \frac{1}{(n-2)^m} c_i + \left( \frac{1}{(n-2)^{m-1}} +1 \right) d_i \right) \\
&= \frac{1}{c_i}\left( \frac{(n-3)}{2(n-2)^{m-1}} c_i + \left( \frac{1}{(n-2)^{m-1}} +1 \right) d_i \right) \\
&\leq \frac{1}{2 (n-2)^{m-2}} + \left( \frac{1}{(n-2)^{m-1}} +1 \right) \frac{d_i}{c_i}.
\end{align*}
\begin{align*}
1 = \frac{c_i -d_i +d_i}{c_i} &= \frac{1}{c_i}\left( \begin{pmatrix}
n-2 \\ 2
\end{pmatrix}c_{i-m} + (n-2)d_{i-m} + d_i \right) \\
&\leq \frac{1}{c_i}\left( \begin{pmatrix}
n-2 \\ 2
\end{pmatrix} \frac{1}{(n-2)^m} c_i + \left( \frac{1}{(n-2)^{m-1}} +1 \right) d_i \right) \\
&= \frac{1}{c_i}\left( \frac{(n-3)}{2(n-2)^{m-1}} c_i + \left( \frac{1}{(n-2)^{m-1}} +1 \right) d_i \right) \\
&\leq \frac{1}{2 (n-2)^{m-2}} + \left( \frac{1}{(n-2)^{m-1}} +1 \right) \frac{d_i}{c_i}.
\end{align*}We put
 \begin{equation*} k := \left( 1 - \frac{1}{2 (n-2)^{m-2}} \right) \cdot \left( \frac{1}{(n-2)^{m-1}} + 1 \right)^{-1}. \end{equation*}
\begin{equation*} k := \left( 1 - \frac{1}{2 (n-2)^{m-2}} \right) \cdot \left( \frac{1}{(n-2)^{m-1}} + 1 \right)^{-1}. \end{equation*} As ![]() $n \geq 3$ and
$n \geq 3$ and ![]() $m \geq 4$, we have k > 0. This proves the claim.
$m \geq 4$, we have k > 0. This proves the claim.
Theorem 5.3. Let (W, S) be 2-spherical and of rank ![]() $n \geq 3$. Then,
$n \geq 3$. Then,  $p_{(W, S)}\left(\frac{1}{n-1}\right) \lt \infty$.
$p_{(W, S)}\left(\frac{1}{n-1}\right) \lt \infty$.
Proof. Let ![]() $m := \max \{4, m_{st} \mid s, t \in S \}$, and let
$m := \max \{4, m_{st} \mid s, t \in S \}$, and let ![]() $(W', S')$ be the Coxeter system of rank n with
$(W', S')$ be the Coxeter system of rank n with ![]() $m_{st}' = m$ for all
$m_{st}' = m$ for all ![]() $s\neq t \in S'$. Using Theorem 5.1, it suffices to show that
$s\neq t \in S'$. Using Theorem 5.1, it suffices to show that
 \begin{equation*} p_{(W', S')}\left( \frac{1}{n-1} \right) \lt \infty. \end{equation*}
\begin{equation*} p_{(W', S')}\left( \frac{1}{n-1} \right) \lt \infty. \end{equation*} By Lemma 5.2, there exists ![]() $k\in \mathbb{R}$ such that
$k\in \mathbb{R}$ such that  $\frac{d_i}{c_i} \geq k \gt 0$ holds for all i > m. We apply the ratio test. We use Lemma 4.5 and compute for
$\frac{d_i}{c_i} \geq k \gt 0$ holds for all i > m. We apply the ratio test. We use Lemma 4.5 and compute for ![]() $i \gt 2m-1$ and
$i \gt 2m-1$ and  $t = \frac{1}{n-1}$:
$t = \frac{1}{n-1}$:
 \begin{align*}
\frac{c_{i+1}t^{i+1}}{c_i t^i} \leq \frac{(n-1) c_i - (n-2)d_{i-m+1}}{(n-1) c_i} \leq 1 - \frac{(n-2) d_{i-m+1}}{(n-1)^m c_{i-m+1}} \leq 1- \frac{n-2}{(n-1)^m} k \lt 1.
\end{align*}
\begin{align*}
\frac{c_{i+1}t^{i+1}}{c_i t^i} \leq \frac{(n-1) c_i - (n-2)d_{i-m+1}}{(n-1) c_i} \leq 1 - \frac{(n-2) d_{i-m+1}}{(n-1)^m c_{i-m+1}} \leq 1- \frac{n-2}{(n-1)^m} k \lt 1.
\end{align*}5.3. Divergence
In this subsection, we prove that the new lower bound  $\frac{1}{n-1}$ for the finiteness of the growth function is optimal for the class of 2-spherical Coxeter systems with a complete Coxeter diagram.
$\frac{1}{n-1}$ for the finiteness of the growth function is optimal for the class of 2-spherical Coxeter systems with a complete Coxeter diagram.
Lemma 5.4. Let (W, S) be 2-spherical and of rank ![]() $n \geq 4$, and assume that the underlying Coxeter diagram is the complete graph. Then
$n \geq 4$, and assume that the underlying Coxeter diagram is the complete graph. Then ![]() $(n-2) c_i \leq d_i + d_{i+1}$.
$(n-2) c_i \leq d_i + d_{i+1}$.
Proof. For i = 0, we have ![]() $c_0 = 1$,
$c_0 = 1$, ![]() $d_0 = 0$ and
$d_0 = 0$ and ![]() $d_1 = n$, and the claim follows. Thus, we can assume i > 0. As in Lemma 4.6, we define
$d_1 = n$, and the claim follows. Thus, we can assume i > 0. As in Lemma 4.6, we define ![]() $N_i := \{(w, s) \in C_i \times S \mid ws \in D_{i+1} \}$ as well as
$N_i := \{(w, s) \in C_i \times S \mid ws \in D_{i+1} \}$ as well as ![]() $N_{i, T} := \{(w, s) \in N_i \mid w\in T \}$ for
$N_{i, T} := \{(w, s) \in N_i \mid w\in T \}$ for ![]() $T \subseteq C_i$. We consider the mapping
$T \subseteq C_i$. We consider the mapping
As before, π is a bijection and we have ![]() $\vert N_i \vert = d_{i+1}$. Moreover, we have
$\vert N_i \vert = d_{i+1}$. Moreover, we have  $N_i = N_{i, D_i} \cup N_{i, C_i \backslash D_i}$ and this union is disjoint. We now count pairs (w, s) in Ni.
$N_i = N_{i, D_i} \cup N_{i, C_i \backslash D_i}$ and this union is disjoint. We now count pairs (w, s) in Ni.
We fix ![]() $w\in D_i$, and we let
$w\in D_i$, and we let ![]() $s_w \in S$ be the unique element with
$s_w \in S$ be the unique element with ![]() $\ell(w s_w) = \ell(w) -1$. Assume that there are
$\ell(w s_w) = \ell(w) -1$. Assume that there are ![]() $r, s, t \in S \backslash \{s_w \}$ pairwise distinct with
$r, s, t \in S \backslash \{s_w \}$ pairwise distinct with ![]() $wr, ws, wt \in C_{i+1} \backslash D_{i+1}$. Similarly, as in Lemma 4.6(b), we deduce
$wr, ws, wt \in C_{i+1} \backslash D_{i+1}$. Similarly, as in Lemma 4.6(b), we deduce ![]() $\ell(wz s_w) = \ell(w)$ for each
$\ell(wz s_w) = \ell(w)$ for each ![]() $z\in \{r, s, t\}$. As
$z\in \{r, s, t\}$. As ![]() $m_{pq} \geq 3$ holds for all
$m_{pq} \geq 3$ holds for all ![]() $p \neq q \in S$, we infer
$p \neq q \in S$, we infer ![]() $\ell(w s_w z) = \ell(w s_w) -1$. As
$\ell(w s_w z) = \ell(w s_w) -1$. As ![]() $\{r, s, t \}$ is not spherical, this is a contradiction and we have for a fixed
$\{r, s, t \}$ is not spherical, this is a contradiction and we have for a fixed ![]() $w\in D_i$ at least n − 3 tuples (w, s) in Ni.
$w\in D_i$ at least n − 3 tuples (w, s) in Ni.
We fix ![]() $w\in C_i \backslash D_i$, and we let
$w\in C_i \backslash D_i$, and we let ![]() $s_w \neq t_w \in S$ be the two elements with
$s_w \neq t_w \in S$ be the two elements with ![]() $\ell(w s_w) = \ell(w)- 1 = \ell(w t_w)$. Assume that there is
$\ell(w s_w) = \ell(w)- 1 = \ell(w t_w)$. Assume that there is ![]() $s\in S \backslash \{s_w, t_w \}$ with
$s\in S \backslash \{s_w, t_w \}$ with ![]() $ws \in C_{i+1} \backslash D_{i+1}$. Then,
$ws \in C_{i+1} \backslash D_{i+1}$. Then, ![]() $\ell(w) \in \{\ell(wss_w), \ell(wst_w) \}$. W.l.o.g. we assume
$\ell(w) \in \{\ell(wss_w), \ell(wst_w) \}$. W.l.o.g. we assume ![]() $\ell(wss_w) = \ell(w)$. But then Corollary 3.3 implies
$\ell(wss_w) = \ell(w)$. But then Corollary 3.3 implies ![]() $\ell(wt_w) = \ell(w) +1$, which is a contradiction. Thus, we have for a fixed
$\ell(wt_w) = \ell(w) +1$, which is a contradiction. Thus, we have for a fixed ![]() $w\in C_i \backslash D_i$ exactly n − 2 tuples (w, s) in Ni (cf. Lemma 4.1). This implies that
$w\in C_i \backslash D_i$ exactly n − 2 tuples (w, s) in Ni (cf. Lemma 4.1). This implies that ![]() $(n-2) c_i - d_i = (n-3) d_i + (n-2) (c_i - d_i) \leq d_{i+1}$.
$(n-2) c_i - d_i = (n-3) d_i + (n-2) (c_i - d_i) \leq d_{i+1}$.
Theorem 5.5. Let (W, S) be of rank ![]() $n \geq 4$, and assume that the underlying Coxeter diagram is the complete graph. Then,
$n \geq 4$, and assume that the underlying Coxeter diagram is the complete graph. Then,  $p_{(W, S)}\left( \frac{1}{n-2} \right) = \infty$.
$p_{(W, S)}\left( \frac{1}{n-2} \right) = \infty$.
Proof. Let ![]() $(W', S')$ be the Coxeter system of rank n with
$(W', S')$ be the Coxeter system of rank n with ![]() $m_{st}' = 3$ for all
$m_{st}' = 3$ for all ![]() $s\neq t \in S'$. Using Theorem 5.1, it suffices to show that
$s\neq t \in S'$. Using Theorem 5.1, it suffices to show that
 \begin{equation*} p_{(W', S')} \left( \frac{1}{n-2} \right) = \infty. \end{equation*}
\begin{equation*} p_{(W', S')} \left( \frac{1}{n-2} \right) = \infty. \end{equation*} As before, we apply the ratio test. Using Lemmas 4.4 and 5.4, we deduce the following for ![]() $i \gt m = 3$ and
$i \gt m = 3$ and  $t = \frac{1}{n-2}$:
$t = \frac{1}{n-2}$:
 \begin{align*}
\frac{c_{i+1} t^{i+1}}{c_i t^i} &= \frac{(n-2) c_i + d_i + d_{i+1}}{2 (n-2) c_i} = \frac{1}{2} + \frac{d_i + d_{i+1}}{2(n-2)c_i} \geq \frac{1}{2} + \frac{1}{2} = 1.
\end{align*}
\begin{align*}
\frac{c_{i+1} t^{i+1}}{c_i t^i} &= \frac{(n-2) c_i + d_i + d_{i+1}}{2 (n-2) c_i} = \frac{1}{2} + \frac{d_i + d_{i+1}}{2(n-2)c_i} \geq \frac{1}{2} + \frac{1}{2} = 1.
\end{align*}Acknowledgements
I am very grateful to Bernhard Mühlherr for stimulating discussions and interesting questions on the topic. I also thank Corentin Bodart and Pierre-Emmanuel Caprace for valuable remarks on an earlier draft. I thank Corentin Bodart for pointing out reference [Reference Arzhantseva and Lysenok2]. Moreover, I would like to thank the anonymous referee for many detailed comments.