Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-09T21:28:43.488Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note about Functions in Lip α

Published online by Cambridge University Press:  20 January 2009

N. Du Plessis
N. Du Plessis
Affiliation:
University of Natal, Durban, South Africa.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note gives a proof of the result:

A necessary and sufficient condition that a trigonometrical series T (x) be the Fourier series of a function 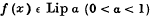is that σn – σm = O(n-n) uniformly in [0, 2π] for all m≤n, where σn is the nth (C, l) mean of T (x).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 10 , Issue 2 , December 1954 , pp. 100
Copyright
Copyright © Edinburgh Mathematical Society 1954

References

Page 100 note 1 Poussin, C. de la Vallée, Leçons sur l'approximation des fonctions (Paris, 1919), §41.Google Scholar

Page 100 note 2 Zygmund, , Trigonometrical Series (1935), p. 62, No. 7.Google Scholar