Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-02T22:05:15.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-linear integral equations for Heun functions

Published online by Cambridge University Press:  20 January 2009

B. D. Sleeman
B. D. Sleeman
Affiliation:
Department of Mathematics, The University, Dundee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some years ago Lambe and Ward (1) and Erdélyi (2) obtained integral equations for Heun polynomials and Heun functions. The integral equations discussed by these authors were of the form

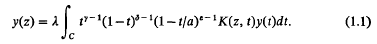
Further, as is well known, the Heun equation includes, among its special cases, Lamé's equation and Mathieu's equation and so (1.1) may be considered a generalisation of the integral equations satisfied by Lamé polynomials and Mathieu functions. However, integral equations of the type (1.1) are not the only ones satisfied by Lamé polynomials; Arscott (3) discussed a class of non- linear integral equations associated with these functions. This paper then is concerned with discussing the existence of non-linear integral equations satisfied by solutions of Heun's equation.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 281 - 289
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1) Lambe, C. G. and Ward, D. R.Some differential equations and associated integral equations, Quart. J. Math. Oxford ser., 5 (1934), 81–97.CrossRefGoogle Scholar
(2) ErdÉlyi, A.Integral equations for Heun functions, Quart. J. Math. Oxford ser., 13 (1942), 107–112.CrossRefGoogle Scholar
(3) Arscott, F. M.Integral equations and relations for Lamé functions, Quart. J. Math. Oxford ser. (2), 15 (1964), 103–115.CrossRefGoogle Scholar
(4) Sleeman, B. D.Integral representations for solutions of Heun's equation, Proc. Camb. Phil. Soc, 65 (1969), 447–459.CrossRefGoogle Scholar
(5) Arscott, F. M., Periodic Differential Equations (Pergamon Press, Oxford, 1964).Google Scholar
(6) Sleeman, B. D.Integral equations and relations for Lamé functions and ellipsoidal wave functions, Proc. Camb. Phil. Soc. 64 (1968), 113–126.CrossRefGoogle Scholar