Article contents
A local mean value theorem for the complex plane
Published online by Cambridge University Press: 20 January 2009
Extract
The equation
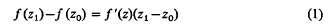
need not have a solution z in the complex plane, even when ƒ is entire. For example, let ƒ(z) = ez, z1 = z0+2kπi. Thus the classical mean value theorem does not extend to the complex plane. McLeod has shown (2) that if ƒ is analytic on the segment joining z1 and z0, then there are points w1 and w2 on the segment such that 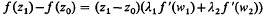 where
where 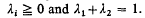
The purpose of this article is to give a local mean value theorem in the complex plane. We show that there is at least one point z satisfying (1), which we will call a mean value point, near z1 and z0 but not necessarily on the segment joining them, provided z1 and z0 are sufficiently close. The proof uses Rouché's Theorem (1).
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 329 - 331
- Copyright
- Copyright © Edinburgh Mathematical Society 1969
References
REFERENCES
- 3
- Cited by


