Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gao, Liu
Chen, Chunfang
and
Zhu, Chuanxi
2020.
Existence of sign-changing solutions for Kirchhoff equations with critical or supercritical nonlinearity.
Applied Mathematics Letters,
Vol. 107,
Issue. ,
p.
106424.
Gao, Liu
Chen, Chunfang
Chen, Jianhua
and
Zhu, Chuanxi
2021.
Sign-Changing Solutions for Fractional Kirchhoff-Type Equations with Critical and Supercritical Nonlinearities.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 3,
Jing, Yongtao
and
Liu, Haidong
2021.
Nonexistence of ground state solutions for generalized quasilinear Schrödinger equations via dual approach.
Journal of Mathematical Physics,
Vol. 62,
Issue. 7,
Zhang, Hui
Meng, Fengjuan
and
Zhang, Jianjun
2022.
Nodal Solutions for Quasilinear Schrödinger Equations with Asymptotically 3-Linear Nonlinearity.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 12,
Huang, Chen
2022.
Multiplicity and asymptotic behavior of solutions for quasilinear elliptic equations with small perturbations.
Journal of Mathematical Analysis and Applications,
Vol. 505,
Issue. 2,
p.
125496.
Zhang, Hui
Liu, Zhisu
Tang, Chun-Lei
and
Zhang, Jianjun
2023.
Existence and multiplicity of sign-changing solutions for quasilinear Schrödinger equations with sub-cubic nonlinearity.
Journal of Differential Equations,
Vol. 365,
Issue. ,
p.
199.
Ma, Yiling
and
Huang, Chen
2025.
Existence of solution for quasilinear Schrödinger equations with general nonlinear terms and non-compact potentials.
Journal of Mathematical Analysis and Applications,
Vol. 546,
Issue. 2,
p.
129216.
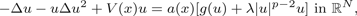 $$-\Delta u - u \Delta u^2 + V(x)u = a(x)[g(u) + \lambda \vert u \vert ^{p-2}u] \hbox{in} {\open R}^N,$$
$$-\Delta u - u \Delta u^2 + V(x)u = a(x)[g(u) + \lambda \vert u \vert ^{p-2}u] \hbox{in} {\open R}^N,$$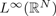 $L</italic>^{\infty}({\open R}^{N})$-estimative.
$L</italic>^{\infty}({\open R}^{N})$-estimative.

