Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Krishna, K. Mahesh
2023.
Absolutely Summing Morphisms between Hilbert C*-Modules and Modular Pietsch Factorization Problem.
SSRN Electronic Journal,
Krishna, K. Mahesh
2023.
Modular Dvoretzky, Type-Cotype, Khinchin-Kahane and Grothendieck Inequality Problems.
SSRN Electronic Journal,


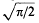 into the final constant. We show that this step can be avoided.
into the final constant. We show that this step can be avoided.