Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hazewinkel, Michiel
2000.
Encyclopaedia of Mathematics.
p.
141.
Xie, Ziqing
2002.
On the Summation of Generalized Arithmetic-Geometric Trigonometric Series.
The Fibonacci Quarterly,
Vol. 40,
Issue. 2,
p.
128.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
459.
Zhao, Xiqiang
and
Ding, Shuangshuang
2004.
A Generalized Summation Rule Related to Stirling Numbers.
The Fibonacci Quarterly,
Vol. 42,
Issue. 3,
p.
194.
GUO, LI
2005.
BAXTER ALGEBRAS, STIRLING NUMBERS AND PARTITIONS.
Journal of Algebra and Its Applications,
Vol. 04,
Issue. 02,
p.
153.
Xu, Aimin
and
Alves, Carlos J. S.
2012.
A Newton Interpolation Approach to Generalized Stirling Numbers.
Journal of Applied Mathematics,
Vol. 2012,
Issue. 1,


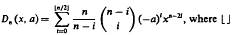 denotes the greatest integer function. In particular, we define
denotes the greatest integer function. In particular, we define 