No CrossRef data available.
Article contents
A counterexample of hermitian liftings
Published online by Cambridge University Press: 20 January 2009
Extract
Let X be a complex Banach space, and let 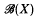 and
and 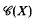 denote respectively the algebras of bounded and compact operators on X. The quotient algebra
denote respectively the algebras of bounded and compact operators on X. The quotient algebra 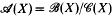 is called the Calkin algebra associated with X. It is known that both
is called the Calkin algebra associated with X. It is known that both 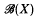 and
and 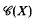 are complex Banach algebras with unit e. For such unital Banach algebras B, set
are complex Banach algebras with unit e. For such unital Banach algebras B, set
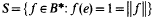
and define the numerical range of x ∈ B as
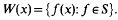
x is said to be hermitian if W(x)⊆R. It is known that
Fact 1. ([4 vol. I, p. 46]) x is hermitian if and only if ‖eiαx‖ = (or ≦)1 for all α ∈ R, where ex is defined by
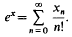
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1989


