Article contents
Characterizations of linear differential systems with a regular singular point
Published online by Cambridge University Press: 20 January 2009
Extract
The linear differential system

where w is a vector with n components and A is an n by n matrix is said to have z = 0 as a regular singular point if there exists a fundamental matrix of the form
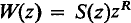
such that S is holomorphic at z = 0 and R is a constant matrix ((1), p. 111; (2), p. 73). For such systems A will have at most a pole at z = 0 and we may write
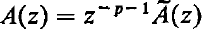
where p is an integer, Ã is holomorphic at z = 0, and Ã(0) ≠ 0. However, the converse is not true. When p ≦ − 1, A is holomorphic at z = 0, and every fundamental matrix is holomorphic at z = 0. If p ≧ 1, the non-negative integer p is called (after Poincaré) the rank of the singularity and there is a significant difference between the cases p = 0 and p ≧ 1. If p = 0 the linear differential system (1) is known to have z = 0 as a regular singular point ((1), p. 111) ; whereas, if p ≧ 1, z = 0 may or may not be a regular singular point.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 2 , December 1972 , pp. 93 - 98
- Copyright
- Copyright © Edinburgh Mathematical Society 1972
References
REFERENCES
- 2
- Cited by


