Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T01:26:39.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic integers as special values of modular units

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 November 2011

Ja Kyung Koo ,
Dong Hwa Shin  and
Dong Sung Yoon
Ja Kyung Koo
Affiliation:
Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 373-1, Korea ([email protected]; [email protected]; [email protected])
Dong Hwa Shin
Affiliation:
Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 373-1, Korea ([email protected]; [email protected]; [email protected])
Dong Sung Yoon
Affiliation:
Department of Mathematical Sciences, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 373-1, Korea ([email protected]; [email protected]; [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 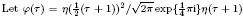, where η(τ) is the Dedekind eta function. We show that if τ0 is an imaginary quadratic argument and m is an odd integer, then 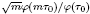is an algebraic integer dividing 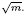This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when K is an imaginary quadratic field and θK is an element of K with Im(θK) > 0 which generates the ring of integers of K over ℤ, we find a sufficient condition on m which ensures that 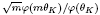is a unit.

Keywords

Dedekind eta functionmodular functionsautomorphic functions

MSC classification

Secondary: 11F20: Dedekind eta function, Dedekind sums 11F03: Modular and automorphic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 1 , February 2012 , pp. 167 - 179
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Berndt, B. C., Ramanujan's notebooks, III (Springer, 1991).CrossRefGoogle Scholar
2.Berndt, B. C., Chan, H. H. and Zhang, L. C., Ramanujan's remarkable product of theta-functions, Proc. Edinb. Math. Soc. 40 (1997), 583–612.CrossRefGoogle Scholar
3.Cox, D. A., Primes of the form x2 + ny2: Fermat, class field, and complex multiplication (Wiley–Interscience, New York, 1989).Google Scholar
4.Deuring, M., Die Klassenkörper der Komplexen Multiplikation, Enzyklopädie der mathematischen Wissenschaften, Volume 12, Issue 10, Part II (Teubner, Stuttgart, 1958).Google Scholar
5.Jung, H. Y., Koo, J. K. and Shin, D. H., Ray class invariants over imaginary quadratic fields, Tohoku Math. J. 63 (2011), 413–426.CrossRefGoogle Scholar
6.Koo, J. K. and Shin, D. H., On some arithmetic properties of Siegel functions, Math. Z. 264 (2010), 137–177.CrossRefGoogle Scholar
7.Kubert, D. and Lang, S., Modular units, Grundlehren der mathematischen Wissenschaften, Volume 244 (Spinger, 1981).Google Scholar
8.Lang, S., Elliptic functions, 2nd edn (Spinger, 1987).CrossRefGoogle Scholar
9.Ramachandra, K., Some applications of Kronecker's limit formula, Annals Math. (2) 80 (1964), 104–148.CrossRefGoogle Scholar
10.Ramanujan, S., Notebooks, two volumes (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
11.Shimura, G., Introduction to the arithmetic theory of automorphic functions (Iwanami Shoten and Princeton University Press, 1971).Google Scholar
12.Stevenhagen, P., Hilbert's 12th problem, complex multiplication and Shimura reciprocity, in Class field theory: its centenary and prospect, Advanced Studies in Pure Mathematics, Volume 30, pp. 161–176 (Mathematical Society of Japan, Tokyo, 2001).Google Scholar