Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T13:55:06.489Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on extensions of multilinear maps defined on multilinear varieties

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  30 April 2021

W. T. Gowers  and
L. Milićević
W. T. Gowers
Affiliation:
Collège de France and University of Cambridge, 11, Place Marcelin-Berthelot, Paris75231, France ([email protected])
L. Milićević
Affiliation:
Mathematical Institute of the Serbian Academy of Sciences and Arts, Kneza Mihaila 36, Belgrade11000, Serbia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $G_1, \ldots , G_k$ be finite-dimensional vector spaces over a prime field $\mathbb {F}_p$. A multilinear variety of codimension at most $d$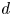 is a subset of $G_1 \times \cdots \times G_k$ defined as the zero set of $d$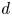 forms, each of which is multilinear on some subset of the coordinates. A map $\phi$ 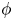defined on a multilinear variety $B$ 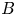is multilinear if for each coordinate $c$ 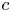and all choices of $x_i \in G_i$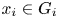, $i\not =c$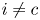, the restriction map $y \mapsto \phi (x_1, \ldots , x_{c-1}, y, x_{c+1}, \ldots , x_k)$ 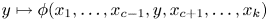is linear where defined. In this note, we show that a multilinear map defined on a multilinear variety of codimension at most $d$ coincides on a multilinear variety of codimension $O_{k}(d^{O_{k}(1)})$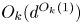 with a multilinear map defined on the whole of $G_1\times \cdots \times G_k$. Additionally, in the case of general finite fields, we deduce similar (but slightly weaker) results.

Keywords

multilinear mapsmultilinear varietiesextensions of maps

MSC classification

Primary: 11P99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 148 - 173
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhowmick, A. and Lovett, S., Bias vs structure of polynomials in large fields, and applications in effective algebraic geometry and coding theory, arXiv preprint (2015), arXiv:1506.02047Google Scholar
Bienvenu, P.-Y. and Lê, T. H., A bilinear Bogolyubov theorem, Eur. J. Comb. 77 (2019), 102–113.10.1016/j.ejc.2018.11.003CrossRefGoogle Scholar
Bienvenu, P.-Y., González-Sánchez, D. and Martínez, Á., A note on the bilinear Bogolyubov theorem: transverse and bilinear sets, Proc. Am. Math. Soc. 148 (2020), 23–31.10.1090/proc/14658CrossRefGoogle Scholar
Gowers, W. T. and Milićević, L., A quantitative inverse theorem for the $U^{4}$ norm over finite fields, arXiv preprint (2017), arXiv:1712.00241Google Scholar
Gowers, W. T. and Milićević, L., A bilinear version of Bogolyubov's theorem, Proc. Am. Math. Soc. 148 (2020), 4695–4704.10.1090/proc/15129CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., Linear forms and higher-degree uniformity for functions on $\mathbb {F}^{n}_p$, Geom. Funct. Anal. 21(1) (2011), 36–69.10.1007/s00039-010-0106-3CrossRefGoogle Scholar
Hosseini, K. and Lovett, S., A bilinear Bogolyubov-Ruzsa lemma with polylogarithmic bounds, Discrete Anal. 10 (2019), 1–14.Google Scholar
Janzer, O., Polynomial bound for the partition rank vs the analytic rank of tensors, Discrete Anal. 7 (2020), 1–18.Google Scholar
Kazhdan, D. and Ziegler, T., Extending weakly polynomial functions from high rank varieties, arXiv preprint (2018), arXiv:1808.09439Google Scholar
Kazhdan, D. and Ziegler, T., Properties of high rank subvarieties of affine spaces, arXiv preprint (2019), arXiv:1902.00767Google Scholar
Lovett, S., The analytic rank of tensors and its applications, Discrete Anal. 7 (2019), 1–10.Google Scholar
Milićević, L., Polynomial bound for partition rank in terms of analytic rank, Geom. Funct. Anal. 29(5) (2019), 1503–1530.10.1007/s00039-019-00505-4CrossRefGoogle Scholar
Naslund, E., The partition rank of a tensor and $k$-right corners in $\mathbb {F}_q^{n}$, J. Comb. Theory, Ser. A 174 (2020), Article 105190.10.1016/j.jcta.2019.105190CrossRefGoogle Scholar