Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T14:21:55.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Low Growth Equational Complexity

Part of: Representation theory of groups Varieties Semigroups

Published online by Cambridge University Press:  25 September 2018

Marcel Jackson
Marcel Jackson*
Affiliation:
Department of Mathematics and Statistics, La Trobe University, Victoria 3086, Australia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The equational complexity function 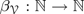$\beta \nu \,:\,{\open N} \to {\open N}$ of an equational class of algebras 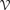bounds the size of equation required to determine the membership of n-element algebras in 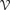. Known examples of finitely generated varieties 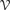with unbounded equational complexity have growth in Ω(nc), usually for c ≥ (1/2). We show that much slower growth is possible, exhibiting 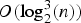$O(\log_{2}^{3}(n))$ growth among varieties of semilattice-ordered inverse semigroups and additive idempotent semirings. We also examine a quasivariety analogue of equational complexity, and show that a finite group has polylogarithmic quasi-equational complexity function, bounded if and only if all Sylow subgroups are abelian.

Keywords

quasivarietygroupequational complexitygrowth

MSC classification

Primary: 08B05: Equational logic, Mal′cev (Mal′tsev) conditions
Secondary: 20M07: Varieties and pseudovarieties of semigroups 20D99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 1 , February 2019 , pp. 197 - 210
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Almeida, J., Finite semigroups and universal algebra (World Scientific, Singapore, 1994).Google Scholar
2.Babai, L., Goodman, A. J., Kantor, W. M., Luks, E. M. and Pálfy, P. P., Short presentations for finite groups, J. Algebra 194 (1997), 79–112.Google Scholar
3.Birkhoff, G., On the structure of abstract algebras, Math. Proc. Camb. Philos. Soc. 31 (1935), 433–454.Google Scholar
4.Burris, S. and Sankappanavar, V. P., A course in universal algebra, Graduate Texts in Mathematics (Springer Verlag, 1981).Google Scholar
5.Eilenberg, S., Automata languages and machines, Pure and Applied Mathematics, Volume B (Academic Press, New York, 1976).Google Scholar
6.Eilenberg, S. and Schützenberger, M.-P., On pseudovarieties, Adv. Math. 19 (1976), 413–418.Google Scholar
7.Gorbunov, V. A., Algebraic theory of quasivarieties (Consultants Bureau, New York, 1998).Google Scholar
8.Higman, G., The orders of relatively free groups, In Proceedings of the International Conference on Theory of Groups, pp. 153–165, (Australian National University, Canberra, 1965).Google Scholar
9.Hirsch, R. and Hodkinson, I., Representability is not decidable for finite relation algebras, Trans. Amer. Math. Soc. 353 (2001), 1403–1425.Google Scholar
10.Howie, J. M., Fundamentals of semigroup theory, 2nd edn (Oxford University Press, New York, 1995).Google Scholar
11.Jackson, M., Flat algebras and the translation of universal Horn logic to equational logic, J. Symb. Logic 73 (2008), 90–128.Google Scholar
12.Jackson, M., Flexible constraint satisfiability and a problem in semigroup theory arXiv:1512.03127, 2015.Google Scholar
13.Jackson, M. and McKenzie, R., Interpreting graph colorability in finite semigroups, Int. J. Algebra Comput. 16 (2006), 119–140.Google Scholar
14.Jackson, M. and McNulty, G. F., The equational complexity of Lyndon's algebra, Algebra Univers. 65 (2011), 243–262.Google Scholar
15.Jackson, M. and Stokes, T., Identities in the algebra of partial maps, Int. J. Algebra Comput. 16 (2006), 1131–1159.Google Scholar
16.Klíma, O., Kunc, M. and Polák, L., Deciding piecewise k-testability, manuscript, 2014.Google Scholar
17.Kozik, M., On some complexity problems in finite algebras, PhD thesis, Vanderbilt University, 2004.Google Scholar
18.Kozik, M., A 2EXPTIME complete varietal membership problem, SIAM J. Comput. 38 (2009), 2443–2467.Google Scholar
19.Kun, G. and Vértesi, V., The membership problem in finite flat hypergraph algebras, Int. J. Algebra Comput. 17 (2007), 449–459.Google Scholar
20.Lawson, M. V., Inverse semigroups: the theory of partial symmetries (World Scientific, 1998.Google Scholar
21.Leech, J., Inverse monoids with a natural semilattice ordering, Proc. Lond. Math. Soc. 70(3) (1995), 146–182.Google Scholar
22.Leech, J., On the foundations of inverse monoids and inverse algebras, Proc. Edinb. Math. Soc. 41(2) (1998), 1–21.Google Scholar
23.McNulty, G. F., Székely, Z. and Willard, R., Equational complexity of the finite algebra membership problem, Int. J. Algebra Comput. 18 (2008), 1283–1319.Google Scholar
24.Neumann, P., Some indecomposable varieties of groups, Q. J. Math. 14 (1963), 46–50.Google Scholar
25.Neumann, H., Varieties of groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, Volume 37 (Springer-Verlag, 1967).Google Scholar
26.Oates, S. and Powell, M. B., Identical relations in finite groups, J. Algebra 1 (1964), 11–39.Google Scholar
27.Ol’s̆anskiıĭ, A. J., Conditional identities of finite groups, Sibirsk. Mat. Zh. 15 (1974), 1409–1413 (in Russian); English version in Siberian Math. J. 15 (1975), 1000–1003.Google Scholar
28.Petrich, M., Inverse semigroups (Wiley, 1984).Google Scholar
29.Rhodes, J. and Steinberg, B., The q-theory of finite semigroups, Springer Monographs in Mathematics (Springer, New York, 2009).Google Scholar
30.Volkov, M. V., Reflexive relations, extensive transformations and piecewise testable languages of a given height, Int. J. Algebra Comput. 14 (2004), 817–827.Google Scholar