Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T04:11:17.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields

Part of: Zeta and $L$-functions: analytic theory Algebraic number theory: global fields Elementary number theory

Published online by Cambridge University Press:  20 August 2018

Alexander Dahl  and
Vítězslav Kala
Alexander Dahl
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ON M3J1P3, Canada ([email protected])
Vítězslav Kala
Affiliation:
University of Göttingen, Mathematisches Institut, Bunsenstr. 3-5, D-37073 Göttingen, Germany Charles University, Faculty of Mathematics and Physics, Department of Algebra, Sokolov-ská 83, 18600 Praha 8, Czech Republic ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a random model to study the distribution of class numbers in special families of real quadratic fields 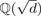${\open Q}(\sqrt d )$ arising from continued fractions. These families are obtained by considering continued fraction expansions of the form 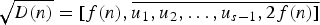$\sqrt {D(n)} = [f(n),\overline {u_1,u_2, \ldots ,u_{s-1} ,2f(n)]} $ with fixed coefficients u1, …, us−1 and generalize well-known families such as Chowla's 4n2 + 1, for which analogous results were recently proved by Dahl and Lamzouri [‘The distribution of class numbers in a special family of real quadratic fields’, Trans. Amer. Math. Soc. (2018), 6331–6356].

Keywords

class numberreal quadratic fieldcontinued fraction familyrandom model

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants
Secondary: 11R11: Quadratic extensions 11M20: Real zeros of $L(s, chi)$; results on $L(1, chi)$ 11A55: Continued fractions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1193 - 1212
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Biró, A., Yokoi's conjecture, Acta Arith. 106 (2003), 85–104.Google Scholar
2.Biró, A. and Granville, A., Zeta functions for ideal classes in real quadratic fields, at s = 0, J. Number Theory 132 (2012), 1807–1829.Google Scholar
3.Biró, A. and Lapkova, K., The class number one problem for the real quadratic fields $Q\left(\sqrt{(an)^2 + 4a} \right)$, Acta Arith. 172 (2016), 117–131.Google Scholar
4.Blomer, V. and Kala, V., Number fields without universal n-ary quadratic forms, Math. Proc. Cambridge Philos. Soc. 159 (2015), 239–252.Google Scholar
5.Dahl, A. and Lamzouri, Y., The distribution of class numbers in a special family of real quadratic fields, Trans. Amer. Math. Soc. (2018), 6331–6356.Google Scholar
6.Friesen, C., On continued fractions of given period, Proc. Amer. Math. Soc. 103 (1988), 8–14.Google Scholar
7.Granville, A. and Soundararajan, K., The distribution of values of L(1, χd), Geom. Funct. Anal. 13(5) (2003), 992–1028.Google Scholar
8.Halter-Koch, F., Continued fractions of given symmetric period, Fibonacci Q. 29 (1991), 298–303.Google Scholar
9.Kala, V., Universal quadratic forms and elements of small norm in real quadratic fields, Bull. Aust. Math. Soc. 94 (2016), 7–14.Google Scholar
10.Kala, V., Norms of indecomposable integers in real quadratic fields, J. Number Theory 166 (2016), 193–207.Google Scholar
11.Kawamoto, F. and Tomita, K., Continued fractions and certain real quadratic fields of minimal type, J. Math. Soc. Japan 60 (2008), 865–903.Google Scholar
12.Lamzouri, Y., Extreme values of class numbers of real quadratic fields, Int. Math. Res. Not. IMRN 22 (2015), 11847–11860.Google Scholar
13.Lamzouri, Y., The distribution of Euler–Kronecker constants of quadratic fields, Math. Anal. App. 432 (2015), 632–653.Google Scholar
14.Lapkova, K., Class number one problem for real quadratic fields of a certain type, Acta Arith. 153 (2012), 281–298.Google Scholar
15.Littlewood, J. E., On the class number of the corpus $P(\sqrt-k)$, Proc. Lond. Math. Soc. 27 (1928), 358–372.Google Scholar
16.Louboutin, S., Continued fractions and real quadratic fields, J. Number Theory 30 (1988), 167–176.Google Scholar
17.McLaughlin, J., Polynomial solutions of Pell's equation and fundamental units in real quadratic fields, J. Lond. Math. Soc. 67(2) (2003), 16–28.Google Scholar
18.Mollin, R. A., A survey of class numbers of quadratic fields in relation to integer solutions of Diophantine equations, in Steiermärkisches Mathematisches Symposium, Stift, Graz, 1986, Volume XVI, pp. 37–48.Google Scholar
19.Perron, O., Die Lehre von den Kettenbrüchen, Band 1 (B. G. Teubner, Stuttgart, 1954).Google Scholar
20.Schinzel, A., On some problems of the arithmetical theory of continued fractions, Acta Arith. 6 (1960/1961), 393–413.Google Scholar
21.Schinzel, A., On some problems of the arithmetical theory of continued fractions II, Acta Arith. 7 (1961/1962), 287–298.Google Scholar
22.Silverman, J. H., The arithmetic of elliptic curves, General Texts in Mathematics, Volume 106 (Springer, 1986).Google Scholar
23.van der Poorten, A. J. and Williams, H. C., On certain continued fraction expansions of fixed period length, Acta Arith. 89 (1999), 23–35.Google Scholar
24.Watkins, M., Class numbers of imaginary quadratic fields, Math. Comput. 73(246) (2004), 907–938.Google Scholar