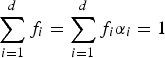Research Article
A CAPACITATED REPLENISHMENT-LIQUIDATION MODEL UNDER CONTRACTUAL AND SPOT MARKETS WITH STOCHASTIC DEMAND
-
- Published online by Cambridge University Press:
- 21 January 2014, pp. 223-269
-
- Article
- Export citation
SOME PROPERTIES OF BINARY SERIES-PARALLEL GRAPHS
-
- Published online by Cambridge University Press:
- 27 June 2014, pp. 565-572
-
- Article
- Export citation
SOME CONVEXITY PROPERTIES OF THE DISTRIBUTION OF LOWER k-RECORD VALUES WITH EXTENSIONS
-
- Published online by Cambridge University Press:
- 17 March 2014, pp. 389-399
-
- Article
-
- You have access
- Export citation
GENERALIZED BIRTHDAY PROBLEMS IN THE LARGE-DEVIATIONS REGIME
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 83-99
-
- Article
- Export citation
ASYMPTOTICS FOR A DISCRETE-TIME RISK MODEL WITH THE EMPHASIS ON FINANCIAL RISK
-
- Published online by Cambridge University Press:
- 27 June 2014, pp. 573-588
-
- Article
- Export citation
SOME REMARKS ON DISTRIBUTED SENSING WITH COSTS
-
- Published online by Cambridge University Press:
- 11 February 2014, pp. 271-277
-
- Article
- Export citation
THE OPTIMAL ADMISSION THRESHOLD IN OBSERVABLE QUEUES WITH STATE DEPENDENT PRICING
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 101-119
-
- Article
- Export citation
BIVARIATE EXTENSIONS OF SKELLAM'S DISTRIBUTION
-
- Published online by Cambridge University Press:
- 17 March 2014, pp. 401-417
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PES volume 28 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
PREVENTION OF CATASTROPHIC FAILURES WITH WEAK FOREWARNING SIGNALS
-
- Published online by Cambridge University Press:
- 19 November 2013, pp. 121-144
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PES volume 28 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 June 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PES volume 28 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PES volume 28 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 June 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
PES volume 28 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
PES volume 28 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PES volume 28 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PES volume 28 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 January 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation