We compute the first two moments and give a recursive formula for the generating function of the first k-record index for a sequence of independent and identically distributed random variables that take on a finite set of possible values. When the random variables have an infinite support, we bound the distribution of the index of the first k-record and show that its mean is infinite.

It is well known that the standard simulated annealing optimization method converges in distribution to the minimum of the cost function if the probability a for accepting an increase in costs goes to 0. α is controlled by the “temperature” parameter, which in the standard setup is a fixed sequence of values converging slowly to 0. We study a more general model in which the temperature may depend on the state of the search process. This allows us to adapt the temperature to the landscape of the cost function. The temperature may temporarily rise such that the process can leave a local optimum more easily. We give weak conditions on the temperature schedules such that the process of solutions finally concentrates near the optimal solutions. We also briefly sketch computational results for the job shop scheduling problem.

This note illustrates that a combination of the approach in our previous papers (Boucherie and Boxma, 1996, Probability in the Engineering and Informational Sciences10: 261–277; Jain and Sigman, 1996, Probability in the Engineering and Informational Sciences 10: 519–531) directly leads to a Pollaczek-Khintchine form for the workload in a queue with negative customers. The same technique is also applied to risk processes with lump additions.

We consider multiclass closed queueing networks. For these networks, a lot of work has been devoted to characterizing and weakening the conditions under which a product-form solution is obtained for the steady-state distribution. From this work, it is known that, under certain conditions, all networks in which each of the stations has either the first-come first-served or the random service discipline lead to the same (product-form expressions for the) steady-state probabilities of the (aggregated) states that for each station and each job class denote the number of jobs in service and the number of jobs in the queue. As a consequence, all these situations also lead to the same throughputs for the different job classes. One of the conditions under which these equivalence results hold states that at each station all job classes must have the same exponential service time distribution. In this paper, it is shown that these equivalence results can be extended to the case with different exponential service times for jobs of different classes, if the network consists of only one single-server or multiserver station. This extension can be made despite of the fact that the network is not a product-form network anymore in that case. The proof is based on the reversibility of the Markov process that is obtained under the random service discipline. By means of a counterexample, it is shown that the extension cannot be made for closed network with two or more stations.

Suppose customers pass through a network of two queues in parallel. A statedependent routing policy gives individuals their quickest journey. The Downs-Thomson effect is any increase in the long-run expected journey time caused by an increase in the service rates. This effect may occur.

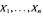Consider a sample from an exponential distribution with unknown parameter θ From the sample, we wish to estimate the entire distribution, 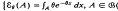(Borel sets). If an estimator 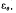is used for 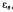, we are concerned with proximity of to 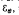, under total variation distance, 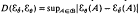the maximum likelihood estimate of θ, define 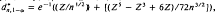, where 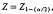, the 1 – (a/2) percentile from the standard normal. Then, 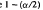. The preceding approximation to the 1 — α percentile of 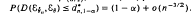is very accurate even for small 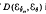n We also consider the problem of obtaining a confidence band for the survival function, possessing minimal maximum width. Finally, a class of estimators of is compared to the maximum likelihood estimator from the viewpoint of total variation distance loss function.

The blood bank system is a typical example of a perishable inventory system. The commodity arrival and customer demand processes are stochastic. However, the stored items have a constant lifetime. In this study, we introduce a diffusion approximation to this system. The stock level is represented by the amount of items arriving during the age of the oldest item; it is assumed to fluctuate as an alternating two-sided regulated Brownian motion between barriers 0 and 1. Hittings of level 0 are outdatings and hittings of level 1 are unsatisfied demands. Also, there are two predetermined switchover levels, a and b, with 0 ≤ a < b ≤ 1. Whenever the stock level process upcrosses level b, the controller generates a switch in the drift from γ = γ0 to γ = γ1, while downcrossings of level a generate switches from γ1 to γ0. A useful martingale is introduced for analyzing the stationary law of the controlled process as well as the total expected discounted cost.

In the standard (S – 1, S) stock model, demand follows a Poisson process. It has appeared to many stock analysts that this model causes an abundance of stock in reality. In case demand is caused by failure or is derived from another process, demand typically does not follow a Poisson process. In this paper, we discuss the (S – 1, S) stock model where demand follows a renewal process and the lead time is deterministic. Moreover, we will extend this to compound renewal demand and multi-echelon inventory systems. Our goal is to show the severe influence of taking the Poisson process for granted.

Consider a population having size X(t) at time t that undergoes a sequence of periods of linear birth, death, and immigration. This paper provides a general method for calculating the absolute probabilities pi, (t) = P(X(t) = i) at any stage in this sequence. In general, the different periods of birth, death, and immigration will have different parameters, although some special cases are also considered where certain parameters are common to all periods. Applications of this model can be found in fiber optics when considering a general cascade of erbium-doped fiber amplifiers. In this application, population size represents photon numbers, transmission through fibers causes attenuation (death), and amplification can be described by a linear birth, death, and immigration process.

The purpose of this paper is to study definitions and characterizations of orders based on reliability measures related with the doubly truncated random variable X[x, y] = (X|x ≤ X ≤ y). The relationship between these orderings and various existing orderings of life distributions are discussed. Moreover, we give two new characterizations of the likelihood ratio order based on double truncation. These new orders complete a general diagram between orders defined from truncation.