Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T08:54:05.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimation of an Exponential Distribution

Published online by Cambridge University Press:  27 July 2009

Mark Brown
Mark Brown
Affiliation:
Department of Mathematics, The City College, Cuny, New York, New York 10031
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a sample 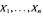from an exponential distribution with unknown parameter θ From the sample, we wish to estimate the entire distribution, 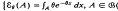(Borel sets). If an estimator 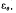is used for 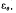, we are concerned with proximity of 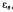to 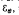, under total variation distance, 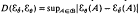the maximum likelihood estimate of θ, define 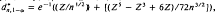, where 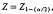, the 1 – (a/2) percentile from the standard normal. Then, 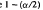. The preceding approximation to the 1 — α percentile of 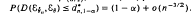is very accurate even for small n We also consider the problem of obtaining a confidence band for the survival function, possessing minimal maximum width. Finally, a class of estimators of 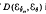is compared to the maximum likelihood estimator from the viewpoint of total variation distance loss function.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 11 , Issue 3 , July 1997 , pp. 341 - 359
Copyright
Copyright © Cambridge University Press 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barbour, A.D., Holst, L., & Janson, S. (1992). Poisson approximation. Oxford Studies in Probability 2. Oxford: Clarendon Press.CrossRefGoogle Scholar
2.Barlow, R.E., Bartholomew, D.J., Bremner, J.M., & Brunk, H.D. (1972). Statistical inference under order restrictions. New York: John Wiley and Sons.Google Scholar
3.Barlow, R.E. & Campo, R. (1975). Total time on test processes with applications to failure data analysis. In Barlow, R.E. et al. (eds.), Reliability and fault tree analysis. Philadelphia: S1AM, pp. 451–481.Google Scholar
4a.Barlow, R.E. & Proschan, F. (1969). A note on tests for monotone failure rate based on incomplete data. Annals of Mathematical Statistics 40: 595–600.CrossRefGoogle Scholar
4b.Barlow, R.E. & Proschan, F. (1975). Statistical theory of reliability and life testing. New York: Holt, Rinehart & Winston.Google Scholar
5.Brown, M. (1995). The distribution of total variation distance with applications to simultaneous confidence intervals. Computers and Operations Research 22(4): 373–381.CrossRefGoogle Scholar
6.Epstein, B. & Sobel, M. (1953). Life testing. Journal of the American Statistical Association 48: 486–502.CrossRefGoogle Scholar
7.Epstein, B. & Sobel, M. (1954). Some theorems relevant to life testing from an exponential distribution. Annals of Mathematical Statistics 25: 373–381.CrossRefGoogle Scholar
8.Gertsbakh, l.B. (1989). Statistical reliability theory. New York: Marcel Dekker.Google Scholar
9.Hall, P. (1992). The bootstrap and Edgeworth expansion. Springer Series in Statistics. New York: Springer-Verlag.CrossRefGoogle Scholar
10.Jensen, J.L. (1995). Saddlepoint approximations. Oxford Statistical Science Series. Oxford: Clarendon Press.CrossRefGoogle Scholar
11.Lehmann, E.L. (1983). Theory of point estimation. New York: John Wiley and Sons.CrossRefGoogle Scholar