Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T09:41:25.919Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOM FINITE SUBSETS WITH EXPONENTIAL DISTRIBUTIONS

Published online by Cambridge University Press:  15 December 2006

Kyle Siegrist
Kyle Siegrist
Affiliation:
Department of Mathematical Sciences, University of Alabama in Huntsville, Huntsville, AL, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S denote the collection of all finite subsets of 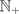. We define an operation on S that makes S into a positive semigroup with set inclusion as the associated partial order. Positive semigroups are the natural home for probability distributions with exponential properties, such as the memoryless and constant rate properties. We show that there are no exponential distributions on S, but that S can be partitioned into subsemigroups, each of which supports a one-parameter family of exponential distributions. We then find the distribution on S that is closest to exponential, in a certain sense. This work might have applications to the problem of selecting a finite sample from a countably infinite population in the most random way.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 21 , Issue 1 , January 2007 , pp. 117 - 132
Copyright
© 2007 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Azlarov, A.T. & Volodin, N.A. (1986). Characterization problems associated with the exponential distribution. Berlin: Springer-Verlag.CrossRef
Högnäs, G. & Mukherjea, A. (1995). Probability measures on semigroups. New York: Plenum Press.CrossRef
Matheron, G. (1975). Random sets and integral geometry. New York: Wiley.
Rowell, G.H. & Siegrist, K. (1998). Relative aging of distributions. Probability in the Engineering and Informational Sciences 12: 469–478.Google Scholar
Siegrist, K. (1994). Exponential distributions on semigroups. Journal of Theoretical Probability 7: 725–737.Google Scholar
Siegrist, K. (2006). Decomposition of exponential distributions on positive semigroups. Journal of Theoretical Probability 19: 204–220.Google Scholar
Siegrist, K. (2007). Exponential and gamma distributions on positive semigroups, with applications to Dirichlet distributions. Bernoulli (to appear).CrossRefGoogle Scholar