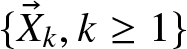1. Introduction
Consider an insurance company, which operates ![]() $m (m\ge2)$ lines of businesses at the same time and uses a common claim-number process. The claim sizes
$m (m\ge2)$ lines of businesses at the same time and uses a common claim-number process. The claim sizes  $\{\vec{X}_k=(X_{1k},\ldots,X_{mk})^T, k\ge 1\}$ form a sequence of independent and identically distributed (i.i.d.) non-negative random vectors with dependent components. Denoted claim arrival times are
$\{\vec{X}_k=(X_{1k},\ldots,X_{mk})^T, k\ge 1\}$ form a sequence of independent and identically distributed (i.i.d.) non-negative random vectors with dependent components. Denoted claim arrival times are  $\tau_k=\sum_{i=1}^{k}\theta_i, k\geq 1$ with
$\tau_k=\sum_{i=1}^{k}\theta_i, k\geq 1$ with ![]() $\tau_0=0$, where
$\tau_0=0$, where ![]() $\{\theta_i, i\ge1\}$ are the claim vectors inter-arrival times. Let
$\{\theta_i, i\ge1\}$ are the claim vectors inter-arrival times. Let ![]() $\{\theta_i, i\geq 1\}$ are identically distributed with a common finite positive mean
$\{\theta_i, i\geq 1\}$ are identically distributed with a common finite positive mean ![]() $1/\lambda$ and finite variance. Then, by time
$1/\lambda$ and finite variance. Then, by time ![]() $t(\ge 0)$, the number of claims is
$t(\ge 0)$, the number of claims is ![]() $N(t)=\sup\{k\ge 1:\tau_k\le t\}.$ In this way, the aggregate amount of claims up to time t are given by the compound sum of the form:
$N(t)=\sup\{k\ge 1:\tau_k\le t\}.$ In this way, the aggregate amount of claims up to time t are given by the compound sum of the form:
 \begin{equation}
\vec{S}(t)=\sum_{k=1}^{N(t)}{\vec{X}_k}=\left(
\begin{array}{c}
\sum_{k=1}^{N(t)}{X_{1k}} \\ \vdots \\ \sum_{k=1}^{N(t)}{X_{mk}} \\
\end{array}
\right),~~~t\ge 0.
\end{equation}
\begin{equation}
\vec{S}(t)=\sum_{k=1}^{N(t)}{\vec{X}_k}=\left(
\begin{array}{c}
\sum_{k=1}^{N(t)}{X_{1k}} \\ \vdots \\ \sum_{k=1}^{N(t)}{X_{mk}} \\
\end{array}
\right),~~~t\ge 0.
\end{equation} If ![]() $\{\theta_i; i\ge 1\}$ and
$\{\theta_i; i\ge 1\}$ and ![]() $\{\vec{X}_{k}; k\ge1\}$ are mutually independent and
$\{\vec{X}_{k}; k\ge1\}$ are mutually independent and ![]() $\{\theta_i; i\ge 1\}$ forms a sequence of
$\{\theta_i; i\ge 1\}$ forms a sequence of ![]() $i.i.d.$ random variable, then we obtain a standard multidimensional renewal risk model.
$i.i.d.$ random variable, then we obtain a standard multidimensional renewal risk model.
It is well known that, with the increasing diversification of insurance companies’ business types, the multidimensional risk model can reflect the influence of different businesses on insurance companies’ solvency more comprehensively. Therefore, the risk theory analysis of multidimensional risk model has attracted the attention of some researchers; see, for example, see, Chen et al. [Reference Chen, Yuen and Ng5], Loukissas [Reference Loukissas12], Fu and Liu [Reference Fu and Liu8], Lu [Reference Lu13], Shen et al. [Reference Shen, Ge and Fu15], Wang and Wang [Reference Wang and Wang19] and references therein.
Note that in above literature, the independent assumption between the claim sizes and the inter-arrival times may be unreasonable in many applications. Think that if the deductible applied to each loss is increased, then the claim sizes will be reduced and the inter-arrival time will be increased since the small losses will be retained by the insured. Therefore, during the last decade, many scholars have addressed this issue by proposing some nonstandard unidimensional renewal risk models, the reader is referred to Asimit and Badescu [Reference Asimit and Badescu1], Chen and Yuen [Reference Chen and Yuen4], Fu and Li [Reference Fu and Li7], Li et al. [Reference Li, Tang and Wu10], and references therein. It should be pointed out that these references study the influence of the dependent structure between the claim sizes and the inter-arrival time only for the unidimensional case. Considering that the multidimensional risk model is more genuine in insurance practice, Shen et al. [Reference Shen, Fu and Zhong14] investigated a class of multidimensional risk models, in which the claim-size vectors and inter-arrival times form a sequence of i.i.d. random pairs and each pair obeys m-dimensional size-dependence structure. In this case, the waiting time distribution of the next large claim-size vector depends only on the size of the latest claim-size vector. However, taking auto insurance as an example, the claim sizes in previous years is an important factor affecting the purchase of insurance, especially the premium in the next few years.
Then, based on the idea of the semi-Markov type dependence structure put forward by Bi and Zhang [Reference Bi and Zhang2], Li et al. [Reference Li, Bi and Zhang11] proposed the regression dependence structure under one-dimensional conditions as follows:
which means that the waiting time of a large claim depends not only on the size of the next claim, but also on the size of previous claims.
Motivated by Li et al. [Reference Li, Bi and Zhang11], we became interested in the regression dependence structure in the multidimensional case, which is more practical. For any fixed ![]() $1\le d \lt n$, suppose that
$1\le d \lt n$, suppose that ![]() $\theta_n (n\ge 1)$ is dependent on
$\theta_n (n\ge 1)$ is dependent on ![]() $\vec{X}_{n-d},\ldots$,
$\vec{X}_{n-d},\ldots$, ![]() $\vec{X}_{n-1}, \vec{X}_{n}$ and independent of
$\vec{X}_{n-1}, \vec{X}_{n}$ and independent of ![]() $\vec{X}_{1}, \vec{X}_{2},\ldots$,
$\vec{X}_{1}, \vec{X}_{2},\ldots$, ![]() $\vec{X}_{n-d-1}, \vec{X}_{n+1},\ldots$, i.e.,
$\vec{X}_{n-d-1}, \vec{X}_{n+1},\ldots$, i.e., ![]() $\vec{X}_{j}$ is only dependent on
$\vec{X}_{j}$ is only dependent on ![]() $\theta_j,\ldots, \theta_{j+d}$. In this case,
$\theta_j,\ldots, \theta_{j+d}$. In this case, ![]() $\{\theta_n, n\ge 1\}$ forms a d-dependent sequence. Then we have
$\{\theta_n, n\ge 1\}$ forms a d-dependent sequence. Then we have
 \begin{align}
\textsf{P}(\theta _k \gt t|\vec{X}_j,j\ge 1) = \begin{cases}
\textsf{P}(\theta _k \gt t|\vec{X}_{1},\ldots,\vec{X}_{k}), & k \le d \\
\textsf{P}(\theta _k \gt t|\vec{X}_{k-d},\ldots,\vec{X}_{k}), & k \gt d, \\
\end{cases}
\end{align}
\begin{align}
\textsf{P}(\theta _k \gt t|\vec{X}_j,j\ge 1) = \begin{cases}
\textsf{P}(\theta _k \gt t|\vec{X}_{1},\ldots,\vec{X}_{k}), & k \le d \\
\textsf{P}(\theta _k \gt t|\vec{X}_{k-d},\ldots,\vec{X}_{k}), & k \gt d, \\
\end{cases}
\end{align}which is an extension of the regression dependence structure in the unidimensional risk models.
Due to the regression dependence structure and the multidimensional risk model being more general, we are interested in the precise large deviations of  $\vec{S}(t)$ in an m-dimensional
$\vec{S}(t)$ in an m-dimensional ![]() $(m\ge2)$ risk model under the regression dependence structure. This paper points out that as long as there exists the strong law of large numbers for N(t) with dependent conditions, the precise large deviations for the multidimensional risk model
$(m\ge2)$ risk model under the regression dependence structure. This paper points out that as long as there exists the strong law of large numbers for N(t) with dependent conditions, the precise large deviations for the multidimensional risk model  $\vec{S}(t)$ with regression size-dependent structure still hold, which is the main result of our paper. The intuition behind it is that if the inter-arrival times
$\vec{S}(t)$ with regression size-dependent structure still hold, which is the main result of our paper. The intuition behind it is that if the inter-arrival times ![]() $\{\theta_n, n\ge 1\}$ is a sequence of identically distributed non-negative random variables with common mean and finite variance, in which
$\{\theta_n, n\ge 1\}$ is a sequence of identically distributed non-negative random variables with common mean and finite variance, in which ![]() $\{\theta_n, n\ge 1\}$ is d-dependent,
$\{\theta_n, n\ge 1\}$ is d-dependent, ![]() $d \ge 1,$ it will be dominated by the consistently varying distributions of the claim sizes. Our assumption extends the dependent structure of the nonstandard multidimensional risk model proposed by Shen et al. [Reference Shen, Fu and Zhong14], and our proof is essentially based on checking the conditions proposed by Li et al. [Reference Li, Bi and Zhang11].
$d \ge 1,$ it will be dominated by the consistently varying distributions of the claim sizes. Our assumption extends the dependent structure of the nonstandard multidimensional risk model proposed by Shen et al. [Reference Shen, Fu and Zhong14], and our proof is essentially based on checking the conditions proposed by Li et al. [Reference Li, Bi and Zhang11].
The rest of this paper is organized as follows. In Section 2, we introduce some preliminary knowledge and give the main result. Finally, in Section 3, we state some lemmas which are very important for the development of the main result and give proof of the main result by establishing corresponding asymptotic upper and lower bounds.
2. Preliminaries and main results
For convenience, we introduce the following notations which will be frequently used throughout this paper. For two positive functions g(x) and h(x), we write ![]() $g(x)\sim h(x)$, if
$g(x)\sim h(x)$, if ![]() $
\lim_{x\rightarrow \infty} g(x)/h(x)=1$,
$
\lim_{x\rightarrow \infty} g(x)/h(x)=1$, ![]() $g(x)\lesssim h(x),$ if
$g(x)\lesssim h(x),$ if ![]() $\lim\sup_{x\rightarrow \infty}g(x)/h(x)\le 1.$ For two positive bivariate functions
$\lim\sup_{x\rightarrow \infty}g(x)/h(x)\le 1.$ For two positive bivariate functions ![]() $g(\cdot ,\cdot )$ and
$g(\cdot ,\cdot )$ and ![]() $h(\cdot ,\cdot )$, we say that
$h(\cdot ,\cdot )$, we say that ![]() $g( x,t ) \lesssim h( x,t )$, as
$g( x,t ) \lesssim h( x,t )$, as ![]() $t\rightarrow\infty$, holds uniformly for
$t\rightarrow\infty$, holds uniformly for ![]() $
x\in \Delta _t\ne \emptyset$, if
$
x\in \Delta _t\ne \emptyset$, if
 \begin{equation*}
\limsup_{t\rightarrow \infty}\sup_{x\in \Delta _t}\frac{g( x,t )}{h( x,t )}\le 1.\end{equation*}
\begin{equation*}
\limsup_{t\rightarrow \infty}\sup_{x\in \Delta _t}\frac{g( x,t )}{h( x,t )}\le 1.\end{equation*} In risk theory, heavy-tailed distributions are often used to model large claim sizes, which play a key role in insurance, financial mathematics and queuing theory. We recall two types of important classes of heavy-tailed distributions. Denote the survival distribution of a random variable with a distribution F by ![]() $\overline {F}(x)=1-F(x) \gt 0$ for all
$\overline {F}(x)=1-F(x) \gt 0$ for all ![]() $x\ge 0.$ By definition, a distribution F on
$x\ge 0.$ By definition, a distribution F on ![]() $[0,\infty)$ belongs to the extended regular variation class, denoted by
$[0,\infty)$ belongs to the extended regular variation class, denoted by ![]() $F\in ERV (-\alpha,-\beta),$ if there are two constants α and β with
$F\in ERV (-\alpha,-\beta),$ if there are two constants α and β with ![]() $0 \lt \alpha\le\beta \lt \infty$ such that for all
$0 \lt \alpha\le\beta \lt \infty$ such that for all ![]() $\upsilon\ge 1$,
$\upsilon\ge 1$,
 \begin{equation*}
\upsilon^{-\beta}\le\liminf_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x )}{\overline{F}( x )}\le\limsup_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x)}{\overline{F}(x)}\le\upsilon^{-\alpha}.
\end{equation*}
\begin{equation*}
\upsilon^{-\beta}\le\liminf_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x )}{\overline{F}( x )}\le\limsup_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x)}{\overline{F}(x)}\le\upsilon^{-\alpha}.
\end{equation*} A larger class is the class ![]() $\mathcal{C}$ of distribution functions with consistent variation (also called intermediate regular variation), characterized by the relation:
$\mathcal{C}$ of distribution functions with consistent variation (also called intermediate regular variation), characterized by the relation:
 \begin{equation*}
\lim_{\upsilon\nearrow 1} \limsup_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x )}{\overline{F}( x )}=\lim_{\upsilon\searrow 1} \liminf_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x)}{\overline{F}(x)}=1.
\end{equation*}
\begin{equation*}
\lim_{\upsilon\nearrow 1} \limsup_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x )}{\overline{F}( x )}=\lim_{\upsilon\searrow 1} \liminf_{x\rightarrow \infty}\frac{\overline{F}(\upsilon x)}{\overline{F}(x)}=1.
\end{equation*} It is easily seen that ![]() $ERV(-\alpha,-\beta)\subset \mathcal{C}$. More discussions of the heavy-tailed distributions can be found in Embrechts et al. [Reference Embrechts, Klüppelberg and Mikosch6]. If
$ERV(-\alpha,-\beta)\subset \mathcal{C}$. More discussions of the heavy-tailed distributions can be found in Embrechts et al. [Reference Embrechts, Klüppelberg and Mikosch6]. If ![]() $F\in\mathcal{C}$, then the upper Matuszewska index of F denoted by
$F\in\mathcal{C}$, then the upper Matuszewska index of F denoted by ![]() $J_{F}^{+}$ is finite [Reference Tang and Tsitsiashvili17]. From Proposition 2.2 in Bingham et al. [Reference Bingham, Goldie and Teugels3], we can see that, for any
$J_{F}^{+}$ is finite [Reference Tang and Tsitsiashvili17]. From Proposition 2.2 in Bingham et al. [Reference Bingham, Goldie and Teugels3], we can see that, for any ![]() $p \gt J_{F}^{+}$, there are two positive constants C and x 0 such that:
$p \gt J_{F}^{+}$, there are two positive constants C and x 0 such that:
 \begin{equation}
\frac{\overline{F}( x )}{\overline{F}( x\upsilon )}\le C\upsilon^p,~{\rm for}~ x\upsilon\ge x\ge x_0.
\end{equation}
\begin{equation}
\frac{\overline{F}( x )}{\overline{F}( x\upsilon )}\le C\upsilon^p,~{\rm for}~ x\upsilon\ge x\ge x_0.
\end{equation}Then one can easily prove that the relation:
holds for all ![]() $p \gt J_{F}^{+}$ [Reference Tang and Tsitsiashvili17].
$p \gt J_{F}^{+}$ [Reference Tang and Tsitsiashvili17].
Thereafter, the following notations will be used throughout this paper. Let ![]() $\mathbb{I}:=\{1,\ldots,m\}$. For a nonempty subset
$\mathbb{I}:=\{1,\ldots,m\}$. For a nonempty subset ![]() $\mathbb{I}^z:=\{i_1,\ldots,i_z\}\subseteq\mathbb{I}$,
$\mathbb{I}^z:=\{i_1,\ldots,i_z\}\subseteq\mathbb{I}$, ![]() $\vec{x}_{\mathbb{I}^z}:=(x_i, i\in \mathbb{I}^z)^T$ is a z-dimensional subvector. As for m-dimensional vectors, we may omit the subscript
$\vec{x}_{\mathbb{I}^z}:=(x_i, i\in \mathbb{I}^z)^T$ is a z-dimensional subvector. As for m-dimensional vectors, we may omit the subscript ![]() $\mathbb{I}^m$ without any confusion. For notational convenience, we state the following assumptions about the claim sizes
$\mathbb{I}^m$ without any confusion. For notational convenience, we state the following assumptions about the claim sizes ![]() $\{\vec{X}_{k}, k\ge 1\}$ and the counting process N(t).
$\{\vec{X}_{k}, k\ge 1\}$ and the counting process N(t).
Assumption 2.1. Suppose that  $\{\vec{X}_k=(X_{1k},\ldots,X_{mk})^T$,
$\{\vec{X}_k=(X_{1k},\ldots,X_{mk})^T$, ![]() $k\ge 1\}$ are identically distributed with
$k\ge 1\}$ are identically distributed with  $\vec{X}=(X_{1},\ldots,X_{m})^T$ and finite mean vector
$\vec{X}=(X_{1},\ldots,X_{m})^T$ and finite mean vector ![]() ${\textsf{E}} \vec{X}=\vec{\mu}=(\mu_{1},\ldots,\mu_{m})^T$. As for the random vector
${\textsf{E}} \vec{X}=\vec{\mu}=(\mu_{1},\ldots,\mu_{m})^T$. As for the random vector ![]() $(X_1,\ldots, X_m)^T,$ suppose that the univariate marginal distribution functions
$(X_1,\ldots, X_m)^T,$ suppose that the univariate marginal distribution functions ![]() $F_i\in \mathcal{C}$(of Xi),
$F_i\in \mathcal{C}$(of Xi), ![]() $i\in \mathbb{I}$, and the joint survival function
$i\in \mathbb{I}$, and the joint survival function ![]() $\overline{F}(\vec{x})={\textsf{P}}(X_i \gt x_i, i\in \mathbb{I})$ is governed by a survival copula
$\overline{F}(\vec{x})={\textsf{P}}(X_i \gt x_i, i\in \mathbb{I})$ is governed by a survival copula ![]() $\hat{C}( \cdot ,\ldots,\cdot )$ satisfying
$\hat{C}( \cdot ,\ldots,\cdot )$ satisfying
 \begin{equation}
\hat{C}(u_i, i\in \mathbb{I}) \le g(m)\prod_{i\in \mathbb{I}}u_i,~(u_i,i\in \mathbb{I})^T\in[0,1]^m,
\end{equation}
\begin{equation}
\hat{C}(u_i, i\in \mathbb{I}) \le g(m)\prod_{i\in \mathbb{I}}u_i,~(u_i,i\in \mathbb{I})^T\in[0,1]^m,
\end{equation} where ![]() $g(\cdot)\ge 1$ is a finite positive function.
$g(\cdot)\ge 1$ is a finite positive function.
Assumption 2.2. For ![]() $n\ge 1$, suppose that
$n\ge 1$, suppose that ![]() $\{\theta_n, n\ge 1\}$ form a d-dependent sequence, for given
$\{\theta_n, n\ge 1\}$ form a d-dependent sequence, for given ![]() $d\ge 1$. Then there exists a nonnegative random variable
$d\ge 1$. Then there exists a nonnegative random variable ![]() $\theta^{\ast }$ with finite mean such that θn conditional on
$\theta^{\ast }$ with finite mean such that θn conditional on  $
(\vec{X}_{n-d} \gt \vec{x},\ldots,\vec{X}_{n} \gt \vec{x})$, is stochastically bounded by
$
(\vec{X}_{n-d} \gt \vec{x},\ldots,\vec{X}_{n} \gt \vec{x})$, is stochastically bounded by ![]() $\theta^{\ast}$ for all
$\theta^{\ast}$ for all  $\vec{x}=(x_{1},\ldots,x_{m})^T \gt \vec{0}$ large enough, i.e., there exists some constant vector
$\vec{x}=(x_{1},\ldots,x_{m})^T \gt \vec{0}$ large enough, i.e., there exists some constant vector ![]() $\vec{x}_0=(x_{10},\ldots,x_{m0})^T$ such that:
$\vec{x}_0=(x_{10},\ldots,x_{m0})^T$ such that:
holds for all ![]() $\vec{x} \gt \vec{x}_0$ and
$\vec{x} \gt \vec{x}_0$ and ![]() $t\in[ 0,\infty)$, where the vector inequality of
$t\in[ 0,\infty)$, where the vector inequality of ![]() $\vec{x} \gt \vec{x}_0$ is operated component-wisely.
$\vec{x} \gt \vec{x}_0$ is operated component-wisely.
Remark 2.1. From Assumption 2.1, it is easy to be seen that ![]() $\overline {F}(\vec{x})=\hat{C}(\overline{F}_i(x_i), i\in \mathbb{I})$ is due to Sklar’s Theorem. Hence, Assumptions 2.1 implies that the random vector
$\overline {F}(\vec{x})=\hat{C}(\overline{F}_i(x_i), i\in \mathbb{I})$ is due to Sklar’s Theorem. Hence, Assumptions 2.1 implies that the random vector ![]() $\vec{X}$ allows the components
$\vec{X}$ allows the components ![]() $X_{1},\ldots,X_{m}$ to depend on each other and satisfy the widely upper orthant dependent. This dependence structure is an important dependence structure introduced by Wang et al. [Reference Wang, Wang and Gao18], covering some common negative and positive dependence structures. Shen et al. [Reference Shen, Niu and Tian16] extend this dependence structure to the multidimensional risk model to describe the dependence relationship between the components of the claim-size vectors. For other copulas that satisfy Assumption 2.1, we refer the reader to Section 3 of Wang et al. [Reference Wang, Wang and Gao18] and Remark 2 of Shen et al. [Reference Shen, Niu and Tian16].
$X_{1},\ldots,X_{m}$ to depend on each other and satisfy the widely upper orthant dependent. This dependence structure is an important dependence structure introduced by Wang et al. [Reference Wang, Wang and Gao18], covering some common negative and positive dependence structures. Shen et al. [Reference Shen, Niu and Tian16] extend this dependence structure to the multidimensional risk model to describe the dependence relationship between the components of the claim-size vectors. For other copulas that satisfy Assumption 2.1, we refer the reader to Section 3 of Wang et al. [Reference Wang, Wang and Gao18] and Remark 2 of Shen et al. [Reference Shen, Niu and Tian16].
Remark 2.2. For the counting process ![]() $N(t), t \ge 0,$ assume
$N(t), t \ge 0,$ assume ![]() $\{\theta_n, n \ge 1\}$ forms a d-dependent sequence. Then
$\{\theta_n, n \ge 1\}$ forms a d-dependent sequence. Then
 \begin{equation}
\frac{N(t)}{t}\rightarrow \lambda,~a.s.
\end{equation}
\begin{equation}
\frac{N(t)}{t}\rightarrow \lambda,~a.s.
\end{equation}and
 \begin{equation}
\frac{{\it{E}}[N(t)]}{t}\rightarrow \lambda.
\end{equation}
\begin{equation}
\frac{{\it{E}}[N(t)]}{t}\rightarrow \lambda.
\end{equation}Going along the similar lines of the proofs of Theorem 4 and 6 in Korchevsky and Petrov [Reference Korchevsky and Petrov9], we can get (8) and (9) immediately. Accordingly, it is easy to see that
 \begin{equation}
\frac{N(t)-\lambda t}{t}\xrightarrow {P}0,~t\rightarrow \infty,
\end{equation}
\begin{equation}
\frac{N(t)-\lambda t}{t}\xrightarrow {P}0,~t\rightarrow \infty,
\end{equation}holds for the counting process in our model.
Now we are in the position to state the main result.
Theorem 2.1. Consider the aggregate amount of claims (1), where ![]() $\{\vec{X}_k, k\ge 1\}$ is a sequence of i.i.d. random vectors with the univariate marginal distribution functions
$\{\vec{X}_k, k\ge 1\}$ is a sequence of i.i.d. random vectors with the univariate marginal distribution functions ![]() $F_i\in \mathcal{C}$(of Xi),
$F_i\in \mathcal{C}$(of Xi), ![]() $i\in \mathbb{I}$. In addition to Assumption 2.1 and Assumption 2.2, suppose that
$i\in \mathbb{I}$. In addition to Assumption 2.1 and Assumption 2.2, suppose that ![]() $\textsf{Var}\theta^{\ast} \lt \infty$. Then, for any given
$\textsf{Var}\theta^{\ast} \lt \infty$. Then, for any given  $\vec{\gamma}=(\gamma_1,\ldots,\gamma_m)^T \gt \vec{0}$,
$\vec{\gamma}=(\gamma_1,\ldots,\gamma_m)^T \gt \vec{0}$,
 \begin{equation}
\textsf{P}(\vec{S}(t)-\vec{\mu} \lambda t \gt \vec{x})\sim (\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i),~~~t\rightarrow \infty,
\end{equation}
\begin{equation}
\textsf{P}(\vec{S}(t)-\vec{\mu} \lambda t \gt \vec{x})\sim (\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i),~~~t\rightarrow \infty,
\end{equation} holds uniformly for all ![]() $\vec{x}\ge \vec{\gamma} t$, i.e.,
$\vec{x}\ge \vec{\gamma} t$, i.e.,
 \begin{equation}
\lim_{t\rightarrow \infty}\sup_{\vec{x}\ge\vec{\gamma}t}\Big|\frac{\textsf{P}(\vec{S}(t)-\vec{\mu} \lambda t \gt \vec{x})}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}-1\Big|=0.
\end{equation}
\begin{equation}
\lim_{t\rightarrow \infty}\sup_{\vec{x}\ge\vec{\gamma}t}\Big|\frac{\textsf{P}(\vec{S}(t)-\vec{\mu} \lambda t \gt \vec{x})}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}-1\Big|=0.
\end{equation}Remark 2.3. Theorem 2.1 proposes the regression dependence structure in multidimensional risk model, which partially extends the results in Shen et al. [Reference Shen, Fu and Zhong14] and Li et al. [Reference Li, Bi and Zhang11]. If θn only depends on ![]() $\vec{X_n}, n \ge 1$, then we can retrieve the corresponding result of Shen et al. [Reference Shen, Fu and Zhong14]. This indicates that both the regression dependence structure between the claim sizes and the inter-arrival times and the dependence components of
$\vec{X_n}, n \ge 1$, then we can retrieve the corresponding result of Shen et al. [Reference Shen, Fu and Zhong14]. This indicates that both the regression dependence structure between the claim sizes and the inter-arrival times and the dependence components of ![]() $\vec{X}_k, k\ge 1$ does not affect the asymptotic behavior of the precise large deviations of
$\vec{X}_k, k\ge 1$ does not affect the asymptotic behavior of the precise large deviations of  $\vec{S}(t)$.
$\vec{S}(t)$.
3. Proofs
In this section, we begin to show the proof of Theorem 2.1. Based on Assumption 2.2 and the definition of regression dependence structure in the multidimensional case, we first construct a generalized multi-delayed renewal counting process. For given ![]() $d\ge1,$ set
$d\ge1,$ set
 \begin{align*}
\tau _{n}^{\ast}=\begin{cases}
\theta _{1}^{\ast}+\cdots +\theta _{n}^{\ast },& n\le md+1\\
\theta _{1}^{\ast}+\cdots +\theta _{md+1}^{\ast }+\sum_{k=md+2}^n{\theta _k},& n \gt md+1,\\
\end{cases}
\end{align*}
\begin{align*}
\tau _{n}^{\ast}=\begin{cases}
\theta _{1}^{\ast}+\cdots +\theta _{n}^{\ast },& n\le md+1\\
\theta _{1}^{\ast}+\cdots +\theta _{md+1}^{\ast }+\sum_{k=md+2}^n{\theta _k},& n \gt md+1,\\
\end{cases}
\end{align*} where the nonnegative random variables ![]() $\theta _{1}^{\ast}\ldots \theta _{md+1}^{\ast }$ are stochastically bounded by the random variable
$\theta _{1}^{\ast}\ldots \theta _{md+1}^{\ast }$ are stochastically bounded by the random variable ![]() $\theta ^{\ast}$, independent of all sources of randomness and identically distributed as θk conditional on
$\theta ^{\ast}$, independent of all sources of randomness and identically distributed as θk conditional on  $(\vec{X}_{k-d} \gt \vec{x},\ldots, \vec{X}_{k} \gt \vec{x}),$ respectively.
$(\vec{X}_{k-d} \gt \vec{x},\ldots, \vec{X}_{k} \gt \vec{x}),$ respectively.
Define the counting process
The following lemma gives the law of large numbers for ![]() $\{N^{\ast}(t), t\ge 0\}.$
$\{N^{\ast}(t), t\ge 0\}.$
Lemma 3.1. In addition to Assumption 2.2, assume that ![]() $\textsf{Var}\theta^{\ast }\in(0,\infty)$. Then, for any
$\textsf{Var}\theta^{\ast }\in(0,\infty)$. Then, for any ![]() $0 \lt \varepsilon \lt \lambda$ and
$0 \lt \varepsilon \lt \lambda$ and ![]() $m\ge 2$,
$m\ge 2$,
 \begin{equation}
\lim_{t\rightarrow \infty}
\textsf{P}\Big(\Big| \frac{N^{\ast}(t)-\lambda t}{t} \Big| \gt \varepsilon\Big) =0.
\end{equation}
\begin{equation}
\lim_{t\rightarrow \infty}
\textsf{P}\Big(\Big| \frac{N^{\ast}(t)-\lambda t}{t} \Big| \gt \varepsilon\Big) =0.
\end{equation}Proof. For a real number y, denote its positive integer part by ![]() $\lfloor y \rfloor$. Observe that, for all t large enough,
$\lfloor y \rfloor$. Observe that, for all t large enough,
 \begin{align}
\textsf{P}(| \frac{N^{\ast}(t)-\lambda t}{t} | \gt \varepsilon)
&=\textsf{P}\Big(N^{\ast}(t) \gt \lambda t+\varepsilon t\Big)+\textsf{P}\Big(N^{\ast}(t) \lt \lambda t-\varepsilon t\Big)
\nonumber\\
&\le \textsf{P}\Big(\sum_{k=md+2}^{\lfloor\lambda t+\varepsilon t\rfloor}\theta_k\le t\Big)+\textsf{P}\Big((md+1)\theta^{\ast}+\sum_{k=md+2}^{\lfloor\lambda t-\varepsilon t\rfloor+1}\theta_k \gt t\Big),
\end{align}
\begin{align}
\textsf{P}(| \frac{N^{\ast}(t)-\lambda t}{t} | \gt \varepsilon)
&=\textsf{P}\Big(N^{\ast}(t) \gt \lambda t+\varepsilon t\Big)+\textsf{P}\Big(N^{\ast}(t) \lt \lambda t-\varepsilon t\Big)
\nonumber\\
&\le \textsf{P}\Big(\sum_{k=md+2}^{\lfloor\lambda t+\varepsilon t\rfloor}\theta_k\le t\Big)+\textsf{P}\Big((md+1)\theta^{\ast}+\sum_{k=md+2}^{\lfloor\lambda t-\varepsilon t\rfloor+1}\theta_k \gt t\Big),
\end{align} where in the last step we used an independent and nonnegative random variable ![]() $\theta^{\ast}$ to bound
$\theta^{\ast}$ to bound ![]() $\theta^{\ast}_k(1\le k\le md+1)$. According to (10) and the law of large numbers for the partial sums
$\theta^{\ast}_k(1\le k\le md+1)$. According to (10) and the law of large numbers for the partial sums ![]() $\sum_{k=1}^{n}\theta_k$, (15) converges to zero as
$\sum_{k=1}^{n}\theta_k$, (15) converges to zero as ![]() $t\rightarrow\infty$, and then we complete the proof.
$t\rightarrow\infty$, and then we complete the proof.
Going along similar lines to proof of Lemma 3 by Shen et al. [Reference Shen, Fu and Zhong14], but with some obvious modifications, we can prove the following lemma immediately.
Lemma 3.2. Let ![]() $\{\vec{X}_k, k\ge 1\}$ be a sequence of i.i.d. random vectors with finite mean vector
$\{\vec{X}_k, k\ge 1\}$ be a sequence of i.i.d. random vectors with finite mean vector ![]() $\vec{\mu}$. Suppose that Assumptions 2.1 is satisfied, then for any
$\vec{\mu}$. Suppose that Assumptions 2.1 is satisfied, then for any  $\vec{\gamma} \gt \vec{0}$,
$\vec{\gamma} \gt \vec{0}$,
 \begin{equation}
\textsf{P}( \vec{S}_n-n\vec{\mu } \gt \vec{x} ) \sim n^m\prod_{i=1}^{m}\overline{F}_i(x_i),~~~ n\rightarrow \infty,
\end{equation}
\begin{equation}
\textsf{P}( \vec{S}_n-n\vec{\mu } \gt \vec{x} ) \sim n^m\prod_{i=1}^{m}\overline{F}_i(x_i),~~~ n\rightarrow \infty,
\end{equation} holds uniformly for all ![]() $\vec{x} \gt \vec{\gamma }n$, where
$\vec{x} \gt \vec{\gamma }n$, where  $\vec{S}_n=(S_{i,n},i\in \mathbb{I})^T:=(\sum_{k=1}^n{X_{i k}},i\in \mathbb{I})^T$.
$\vec{S}_n=(S_{i,n},i\in \mathbb{I})^T:=(\sum_{k=1}^n{X_{i k}},i\in \mathbb{I})^T$.
Lemma 3.3. Consider the aggregate amount of claims (1). Suppose that Assumptions 2.1 satisfies  $J_{F_i}^{+} \lt \infty, i\in \mathbb{I}$. Then for every
$J_{F_i}^{+} \lt \infty, i\in \mathbb{I}$. Then for every  $p \gt \max \{J_{F_1}^{+},\ldots, J_{F_m}^{+} \}
$, there exists some constant C > 0 (whose value may vary from place to place) such that, for any
$p \gt \max \{J_{F_1}^{+},\ldots, J_{F_m}^{+} \}
$, there exists some constant C > 0 (whose value may vary from place to place) such that, for any ![]() $n\ge md+1$ and
$n\ge md+1$ and ![]() $t\ge 0$,
$t\ge 0$,
 \begin{align}
\textsf{P}\Big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x},\tau_n\le t}\Big)
\le C\sum_{k=1}^{m}\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k} n^{mp+k}\textsf{P}(\tau _{n-md-1}\le t),
\end{align}
\begin{align}
\textsf{P}\Big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x},\tau_n\le t}\Big)
\le C\sum_{k=1}^{m}\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k} n^{mp+k}\textsf{P}(\tau _{n-md-1}\le t),
\end{align} holds for all ![]() $\vec{x}\ge \vec{0}$.
$\vec{x}\ge \vec{0}$.
Proof. Let ![]() $\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}$ be an arbitrary partition of
$\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}$ be an arbitrary partition of ![]() $\mathbb{I}, 1\le k\le m$, that is,
$\mathbb{I}, 1\le k\le m$, that is,
 \begin{equation}
\bigcup_{i=1}^{k}\mathbb{I}^i=\mathbb{I}, \mathbb{I}^i\cap\mathbb{I}^j=\emptyset, i\neq j.
\end{equation}
\begin{equation}
\bigcup_{i=1}^{k}\mathbb{I}^i=\mathbb{I}, \mathbb{I}^i\cap\mathbb{I}^j=\emptyset, i\neq j.
\end{equation} Let ![]() $\mathcal{J}_k$ be the set of all partitions with k subsets of
$\mathcal{J}_k$ be the set of all partitions with k subsets of ![]() $\mathbb{I}, 1\le k\le m$. The summation
$\mathbb{I}, 1\le k\le m$. The summation![]() $\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}$ is for all partitions
$\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}$ is for all partitions ![]() $\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}, 1\le k\le m$ over the collection
$\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}, 1\le k\le m$ over the collection ![]() $\mathcal{J}_k$. From the non-negativity of θ and the independence between θn and
$\mathcal{J}_k$. From the non-negativity of θ and the independence between θn and ![]() $\vec{X}_1, \vec{X}_2, \ldots, \vec{X}_{n-d-1},$
$\vec{X}_1, \vec{X}_2, \ldots, \vec{X}_{n-d-1},$ ![]() $\vec{X}_{n+1}, \ldots,$ we can get
$\vec{X}_{n+1}, \ldots,$ we can get
 \begin{align}
&\textsf{P}\Big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x},\tau_n\le t}\Big)
\nonumber\\ &\le\textsf{P}\Big(\bigcup_{j_i=1}^{n}(X_{i j_i} \gt \frac{x_i}{n}),
\tau_n\le t, i\in \mathbb{I}\Big)
\nonumber\\
&\le\sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}\big(X_{i j_i} \gt \frac{x_i}{n},
\tau_n\le t, i\in \mathbb{I}\big)
\nonumber\\
&=\sum_{j=1}^{n}\textsf{P}\big(X_{i j} \gt \frac{x_i}{n},
\tau_n\le t, i\in \mathbb{I}\big)
\nonumber\\
&\hspace{1.5cm}+\sum_{k=2}^{m}\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{\substack{1\le j_s\neq j_l\le n, s\neq l,\\ s,l=1,\ldots,k}}\textsf{P}\big(\bigcap_{h=1}^{k}
\{X_{q j_h} \gt \frac{x_q}{n},q\in \mathbb{I}^h\},
\tau_n\le t\big)
\nonumber\\
&=:I_1(\vec{x},t)+\sum_{k=2}^{m}I_{k}(\vec{x},t).
\end{align}
\begin{align}
&\textsf{P}\Big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x},\tau_n\le t}\Big)
\nonumber\\ &\le\textsf{P}\Big(\bigcup_{j_i=1}^{n}(X_{i j_i} \gt \frac{x_i}{n}),
\tau_n\le t, i\in \mathbb{I}\Big)
\nonumber\\
&\le\sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}\big(X_{i j_i} \gt \frac{x_i}{n},
\tau_n\le t, i\in \mathbb{I}\big)
\nonumber\\
&=\sum_{j=1}^{n}\textsf{P}\big(X_{i j} \gt \frac{x_i}{n},
\tau_n\le t, i\in \mathbb{I}\big)
\nonumber\\
&\hspace{1.5cm}+\sum_{k=2}^{m}\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{\substack{1\le j_s\neq j_l\le n, s\neq l,\\ s,l=1,\ldots,k}}\textsf{P}\big(\bigcap_{h=1}^{k}
\{X_{q j_h} \gt \frac{x_q}{n},q\in \mathbb{I}^h\},
\tau_n\le t\big)
\nonumber\\
&=:I_1(\vec{x},t)+\sum_{k=2}^{m}I_{k}(\vec{x},t).
\end{align} Inequality (4) implies that, for any fixed  $p \gt \max\{J_{F_i}^{+},i\in\mathbb{I}\}$, there are some large positive constant C and some constant vector
$p \gt \max\{J_{F_i}^{+},i\in\mathbb{I}\}$, there are some large positive constant C and some constant vector ![]() $\vec{x}_0$ such that the inequality
$\vec{x}_0$ such that the inequality ![]() $\textsf{P}( X_i \gt {x_i}/{n}) \le Cn^p\overline{F_i}(x_i), i\in \mathbb{I}$ holds for all
$\textsf{P}( X_i \gt {x_i}/{n}) \le Cn^p\overline{F_i}(x_i), i\in \mathbb{I}$ holds for all ![]() $\vec{x}\ge n\vec{x}_{0}$ (c.f. [Reference Chen and Yuen4]). Then, for
$\vec{x}\ge n\vec{x}_{0}$ (c.f. [Reference Chen and Yuen4]). Then, for ![]() $I_1(x,t)$, it follows from the above mentioned multidimensional regression property and Assumption 2.1, an upper bound can be constructed as follows:
$I_1(x,t)$, it follows from the above mentioned multidimensional regression property and Assumption 2.1, an upper bound can be constructed as follows:
 \begin{align}
I_1(\vec{x},t)
&\le\sum_{j=1}^{n}\textsf{P}\big(X_{i j} \gt \frac{x_i}{n},
\sum_{1\le z\neq j\le n}\theta_z\le t , i\in \mathbb{I}\big)
\nonumber\\
&\le n\textsf{P}(X_{i} \gt \frac{x_i}{n}, i\in \mathbb{I})\textsf{P}( \tau _{n-d-1}\le t )
\nonumber\\
&\le Cn^{mp+1}g(m)\prod_{i=1}^{m}\overline {F_i}(x_i)\textsf{P}( \tau _{n-d-1}\le t).
\end{align}
\begin{align}
I_1(\vec{x},t)
&\le\sum_{j=1}^{n}\textsf{P}\big(X_{i j} \gt \frac{x_i}{n},
\sum_{1\le z\neq j\le n}\theta_z\le t , i\in \mathbb{I}\big)
\nonumber\\
&\le n\textsf{P}(X_{i} \gt \frac{x_i}{n}, i\in \mathbb{I})\textsf{P}( \tau _{n-d-1}\le t )
\nonumber\\
&\le Cn^{mp+1}g(m)\prod_{i=1}^{m}\overline {F_i}(x_i)\textsf{P}( \tau _{n-d-1}\le t).
\end{align} As for ![]() $I_k(\vec{x},t), 2\le k \le m$, using (4) and Assumption 2.1 again, we have
$I_k(\vec{x},t), 2\le k \le m$, using (4) and Assumption 2.1 again, we have
 \begin{align}
I_k(\vec{x},t)&\le \sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{\substack{1\le j_s\neq j_l\le n, s\neq l,\\ s,l=1,\ldots,k}}\textsf{P}\Big(\bigcap_{h=1}^{k}\{X_{q j_h} \gt \frac{x_q}{n},q\in \mathbb{I}^h\},
\sum_{1\le z\neq j_1,\ldots, j_k\le n}\theta_z\le t\Big)
\nonumber\\
&\le\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}
\prod_{h=1}^{k}(n-h+1)\hat{C}_{\mathbb{I}^h}\big(\overline F(\frac{x_q}{n}),q\in \mathbb{I}^h\big)\textsf{P}(\tau _{n-kd-1}\le t)
\nonumber\\
&\le\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\prod_{h=1}^{k}(n-h+1)
\Big[g(m)\prod_{q\in \mathbb{I}^h}(Cn^p\overline F(x_q))\Big]\textsf{P}(\tau _{n-kd-1}\le t)
\nonumber\\
&\le C\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k} n^{mp+k}\textsf{P}(\tau _{n-kd-1}\le t),
\end{align}
\begin{align}
I_k(\vec{x},t)&\le \sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{\substack{1\le j_s\neq j_l\le n, s\neq l,\\ s,l=1,\ldots,k}}\textsf{P}\Big(\bigcap_{h=1}^{k}\{X_{q j_h} \gt \frac{x_q}{n},q\in \mathbb{I}^h\},
\sum_{1\le z\neq j_1,\ldots, j_k\le n}\theta_z\le t\Big)
\nonumber\\
&\le\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}
\prod_{h=1}^{k}(n-h+1)\hat{C}_{\mathbb{I}^h}\big(\overline F(\frac{x_q}{n}),q\in \mathbb{I}^h\big)\textsf{P}(\tau _{n-kd-1}\le t)
\nonumber\\
&\le\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\prod_{h=1}^{k}(n-h+1)
\Big[g(m)\prod_{q\in \mathbb{I}^h}(Cn^p\overline F(x_q))\Big]\textsf{P}(\tau _{n-kd-1}\le t)
\nonumber\\
&\le C\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k} n^{mp+k}\textsf{P}(\tau _{n-kd-1}\le t),
\end{align} where the identically distributed of θz and the independence between Xj and ![]() $\theta_1,\ldots, \theta_{j-1}, \theta_{j+d+1},\ldots$ are used in the first step, and then we complete the proof.
$\theta_1,\ldots, \theta_{j-1}, \theta_{j+d+1},\ldots$ are used in the first step, and then we complete the proof.
Now, we begin to show the proofs of Theorem 2.1.
In what follows, every limit relation is understood as valid uniformly for all ![]() $\vec{x}\ge \vec{\gamma }t$ as
$\vec{x}\ge \vec{\gamma }t$ as ![]() $t\rightarrow \infty$. Note that Theorem 2.1 follows immediate once we show that
$t\rightarrow \infty$. Note that Theorem 2.1 follows immediate once we show that
 \begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x})\lesssim (\lambda t )^m\prod_{i=1}^{m}\overline{F}_i(x_i),
\end{align}
\begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x})\lesssim (\lambda t )^m\prod_{i=1}^{m}\overline{F}_i(x_i),
\end{align}and
 \begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x} ) \gt rsim (\lambda t )^m\prod_{i=1}^{m}\overline{F}_i(x_i).
\end{align}
\begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x} ) \gt rsim (\lambda t )^m\prod_{i=1}^{m}\overline{F}_i(x_i).
\end{align} We first show the asymptotic upper bound. For small ![]() $\varepsilon \in (0,1)$, we have
$\varepsilon \in (0,1)$, we have
 \begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x})&=\textsf{P}\big(\vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x},N(t)\le\lambda t+\varepsilon t\big)
\nonumber\\
&\hspace{1.5cm}+\textsf{P}\big(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x},N(t) \gt \lambda t+\varepsilon t \big)
\nonumber\\
&=:K_1(\vec{x},t)+K_2(\vec{x},t).
\end{align}
\begin{align}
\textsf{P}(\vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x})&=\textsf{P}\big(\vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x},N(t)\le\lambda t+\varepsilon t\big)
\nonumber\\
&\hspace{1.5cm}+\textsf{P}\big(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x},N(t) \gt \lambda t+\varepsilon t \big)
\nonumber\\
&=:K_1(\vec{x},t)+K_2(\vec{x},t).
\end{align} As for ![]() $K_1(\vec{x},t)$, it follows from Lemma 3.2 and Assumption 2.1 that:
$K_1(\vec{x},t)$, it follows from Lemma 3.2 and Assumption 2.1 that:
 \begin{align}
K_1(\vec{x},t)&\le \textsf{P}\big(\vec{S}_{\lfloor \lambda t+\varepsilon t \rfloor} -\vec{\mu }\lambda t \gt \vec{x}\big)
\nonumber\\
&=\textsf{P}\big( \vec{S}_{\lfloor \lambda t+\varepsilon t\rfloor} -\vec{\mu}\lfloor \lambda t+\varepsilon t\rfloor \gt \vec{x}+\vec{\mu }\lambda t-\vec{\mu }\lfloor \lambda t+\varepsilon t \rfloor \big)
\nonumber\\
&\sim \big(\lfloor\lambda t+\varepsilon t\rfloor\big)^m\prod_{i=1}^{m}\overline{F}_i( x_{i}^{\prime})
\nonumber\\
&\lesssim \big(\lambda t+\varepsilon t\big)^m\prod_{i=1}^{m}\overline{F}_i\big( ( 1-\varepsilon\mu_i/\gamma_i)x_i \big),
\end{align}
\begin{align}
K_1(\vec{x},t)&\le \textsf{P}\big(\vec{S}_{\lfloor \lambda t+\varepsilon t \rfloor} -\vec{\mu }\lambda t \gt \vec{x}\big)
\nonumber\\
&=\textsf{P}\big( \vec{S}_{\lfloor \lambda t+\varepsilon t\rfloor} -\vec{\mu}\lfloor \lambda t+\varepsilon t\rfloor \gt \vec{x}+\vec{\mu }\lambda t-\vec{\mu }\lfloor \lambda t+\varepsilon t \rfloor \big)
\nonumber\\
&\sim \big(\lfloor\lambda t+\varepsilon t\rfloor\big)^m\prod_{i=1}^{m}\overline{F}_i( x_{i}^{\prime})
\nonumber\\
&\lesssim \big(\lambda t+\varepsilon t\big)^m\prod_{i=1}^{m}\overline{F}_i\big( ( 1-\varepsilon\mu_i/\gamma_i)x_i \big),
\end{align} where ![]() $x_{i}^{\prime}=x_i+\mu _i\lambda t-\mu_i\lfloor \lambda t+\varepsilon t\rfloor\ge (1-{\varepsilon\mu_i}/{\gamma _i})x_i$ for
$x_{i}^{\prime}=x_i+\mu _i\lambda t-\mu_i\lfloor \lambda t+\varepsilon t\rfloor\ge (1-{\varepsilon\mu_i}/{\gamma _i})x_i$ for ![]() $x_i\ge\gamma_i t$,
$x_i\ge\gamma_i t$, ![]() $i\in \mathbb{I}$. Then applying the condition
$i\in \mathbb{I}$. Then applying the condition ![]() $F_i\in \mathcal{C}$,
$F_i\in \mathcal{C}$, ![]() $i\in \mathbb{I}$, we have
$i\in \mathbb{I}$, we have
 \begin{align}
\lim_{\varepsilon \downarrow 0} \limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{K_1(\vec{x},t)}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}\le 1.
\end{align}
\begin{align}
\lim_{\varepsilon \downarrow 0} \limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{K_1(\vec{x},t)}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}\le 1.
\end{align} Next, we estimate ![]() $K_2(\vec{x},t)$. By (4), for every
$K_2(\vec{x},t)$. By (4), for every  $p \gt \max \{J_{F_i}^{+}, i\in \mathbb{I} \}$, it follows from Assumption 2.1, we have
$p \gt \max \{J_{F_i}^{+}, i\in \mathbb{I} \}$, it follows from Assumption 2.1, we have
 \begin{align}
K_2(\vec{x},t)&=\sum_{n \gt \lambda t+\varepsilon t}\textsf{P}\big(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x},N(t)=n\big)
\nonumber\\
&\le\sum_{n \gt \lambda t+\varepsilon t}\textsf{P}\big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x}},
\tau_n\le t\big)
\nonumber\\
&\le C\sum_{k=1}^{m}\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{n \gt \lambda t+\varepsilon t} n^{mp+k}\textsf{P}(\tau _{n-md-1}\le t),
\end{align}
\begin{align}
K_2(\vec{x},t)&=\sum_{n \gt \lambda t+\varepsilon t}\textsf{P}\big(\vec{S}(t)-\vec{\mu}\lambda t \gt \vec{x},N(t)=n\big)
\nonumber\\
&\le\sum_{n \gt \lambda t+\varepsilon t}\textsf{P}\big( \sum_{k=1}^n{\vec{X}_k \gt \vec{x}},
\tau_n\le t\big)
\nonumber\\
&\le C\sum_{k=1}^{m}\big(g(m)\big)^k\prod_{i=1}^{m}\overline F_i(x_i)\sum_{\{\mathbb{I}^1,\ldots,\mathbb{I}^k\}\in \mathcal{J}_k}\sum_{n \gt \lambda t+\varepsilon t} n^{mp+k}\textsf{P}(\tau _{n-md-1}\le t),
\end{align}where Lemmas 3.3 is used in the third step. Then, by Lemma 3.3 of Li et al. [Reference Li, Bi and Zhang11], we have
 \begin{align}
K_2(\vec{x},t)=o(t)\prod_{i=1}^{m}\overline {F}_i(x_i).
\end{align}
\begin{align}
K_2(\vec{x},t)=o(t)\prod_{i=1}^{m}\overline {F}_i(x_i).
\end{align}This, coupled with (26), gives (22).
In the sequel, we show the asymptotic lower bound. Notice that for any ![]() $\varepsilon \in (0,1)$ small enough and ν > 1, we get
$\varepsilon \in (0,1)$ small enough and ν > 1, we get
 \begin{align}
&\textsf{P}( \vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x} )
\nonumber\\
&\ge \sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}{\textsf{P}( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, N(t)=n)}
\nonumber\\
&\ge \sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}\textsf{P}\Big( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, \max_{1\le j_i\le n} X_{i j_i} \gt \nu x_i, N(t)=n, i\in \mathbb{I}\Big).
\end{align}
\begin{align}
&\textsf{P}( \vec{S}(t)-\vec{\mu }\lambda t \gt \vec{x} )
\nonumber\\
&\ge \sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}{\textsf{P}( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, N(t)=n)}
\nonumber\\
&\ge \sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}\textsf{P}\Big( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, \max_{1\le j_i\le n} X_{i j_i} \gt \nu x_i, N(t)=n, i\in \mathbb{I}\Big).
\end{align}By virtue of Bonferroni’s inequality, we can get
 \begin{align}
&\textsf{P}\Big( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, \max_{1\le j_i\le n} X_{i j_i} \gt \nu x_i, N(t)=n, i\in \mathbb{I}\Big)
\nonumber\\
&\ge \sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}(\vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I})
\nonumber\\
&\hspace{1.5cm}-\sum_{1\le j_1,\ldots,j_m, p_1\le n, j_1\neq p_1}{\textsf{P}(X_{1 p_1} \gt \nu x_1, X_{i j_i} \gt \nu x_i, N(t)= n, i\in \mathbb{I})}
\nonumber\\
&\hspace{2.5cm}\cdots
\nonumber\\
&\hspace{2.5cm}-\sum_{1\le j_1,\ldots,j_m, p_m\le n, j_m\neq p_m}{\textsf{P}(X_{m p_m} \gt \nu x_m, X_{i j_i} \gt \nu x_i, N(t)= n, i\in \mathbb{I})}
\nonumber\\
&=:J_0(\vec{x},t)-J_1(\vec{x},t)-\cdots-J_m(\vec{x},t).
\end{align}
\begin{align}
&\textsf{P}\Big( \vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, \max_{1\le j_i\le n} X_{i j_i} \gt \nu x_i, N(t)=n, i\in \mathbb{I}\Big)
\nonumber\\
&\ge \sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}(\vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I})
\nonumber\\
&\hspace{1.5cm}-\sum_{1\le j_1,\ldots,j_m, p_1\le n, j_1\neq p_1}{\textsf{P}(X_{1 p_1} \gt \nu x_1, X_{i j_i} \gt \nu x_i, N(t)= n, i\in \mathbb{I})}
\nonumber\\
&\hspace{2.5cm}\cdots
\nonumber\\
&\hspace{2.5cm}-\sum_{1\le j_1,\ldots,j_m, p_m\le n, j_m\neq p_m}{\textsf{P}(X_{m p_m} \gt \nu x_m, X_{i j_i} \gt \nu x_i, N(t)= n, i\in \mathbb{I})}
\nonumber\\
&=:J_0(\vec{x},t)-J_1(\vec{x},t)-\cdots-J_m(\vec{x},t).
\end{align} Let  $\vec{S}_{n,(j_1,\cdots, j_k)}=\vec{S}_{n}-\sum_{i=1}^{k}\vec{X}_{j_i}$.
$\vec{S}_{n,(j_1,\cdots, j_k)}=\vec{S}_{n}-\sum_{i=1}^{k}\vec{X}_{j_i}$.
Then we can derive that
 \begin{align}
J_0(\vec{x},t)&= \sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}(\vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I})
\nonumber\\
&\ge \sum_{\substack{1\le j_l\neq j_s\le n, l\neq s\\s,l=1,\ldots,m}}\textsf{P}\big(\vec{S}_{n,(j_1,\cdots, j_m)}-\vec{\mu }\lambda t \gt (1-\nu)\vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I}\big)
\nonumber\\
&\ge\sum_{\substack{1\le j_l\neq j_s\le n, l\neq s\\s,l=1,\ldots,m}}\{\textsf{P}\big(\vec{S}_{n,(\,j_1,\cdots, j_m)}-\vec{\mu }\lambda t \gt (1-\nu)\vec{x}, N(t)=n|\vec{X}_{j_i} \gt \nu \vec{x}, i\in \mathbb{I}\big)\textsf{P}(X_{i j_i} \gt \nu x_i,i\in \mathbb{I})\}
\nonumber\\
&\ge n(n-1)\cdots (n-m+1)\textsf{P}\big(\vec{S}_{n,
(1,2\ldots,m)}-\vec{\mu}\lambda t \gt (1-\nu )\vec{x},N^{\ast}(t)=n\big)\prod_{i=1}^{m}\overline{F}_i(\nu x_i),
\end{align}
\begin{align}
J_0(\vec{x},t)&= \sum_{1\le j_1,\ldots,j_m\le n}\textsf{P}(\vec{S}_n-\vec{\mu }\lambda t \gt \vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I})
\nonumber\\
&\ge \sum_{\substack{1\le j_l\neq j_s\le n, l\neq s\\s,l=1,\ldots,m}}\textsf{P}\big(\vec{S}_{n,(j_1,\cdots, j_m)}-\vec{\mu }\lambda t \gt (1-\nu)\vec{x}, X_{i j_i} \gt \nu x_i, N(t) =n, i\in \mathbb{I}\big)
\nonumber\\
&\ge\sum_{\substack{1\le j_l\neq j_s\le n, l\neq s\\s,l=1,\ldots,m}}\{\textsf{P}\big(\vec{S}_{n,(\,j_1,\cdots, j_m)}-\vec{\mu }\lambda t \gt (1-\nu)\vec{x}, N(t)=n|\vec{X}_{j_i} \gt \nu \vec{x}, i\in \mathbb{I}\big)\textsf{P}(X_{i j_i} \gt \nu x_i,i\in \mathbb{I})\}
\nonumber\\
&\ge n(n-1)\cdots (n-m+1)\textsf{P}\big(\vec{S}_{n,
(1,2\ldots,m)}-\vec{\mu}\lambda t \gt (1-\nu )\vec{x},N^{\ast}(t)=n\big)\prod_{i=1}^{m}\overline{F}_i(\nu x_i),
\end{align} where ![]() $N^{\ast}(t)$ is a generalized multi-delayed renewal counting process constructed as in (13). By choosing positive ɛ small enough such that
$N^{\ast}(t)$ is a generalized multi-delayed renewal counting process constructed as in (13). By choosing positive ɛ small enough such that ![]() $( 1-\varepsilon) \lambda \mu _i-\lambda \mu _i \gt (1-\nu) \gamma _i$ for
$( 1-\varepsilon) \lambda \mu _i-\lambda \mu _i \gt (1-\nu) \gamma _i$ for ![]() $i\in \mathbb{I}$, then it follows from the laws of large numbers for the partial sums
$i\in \mathbb{I}$, then it follows from the laws of large numbers for the partial sums  $\vec{S}_{n,(1,\ldots, m)}, n\ge 1,$
$\vec{S}_{n,(1,\ldots, m)}, n\ge 1,$
 \begin{align}
\textsf{P}\big(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x}\big)=1.
\end{align}
\begin{align}
\textsf{P}\big(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x}\big)=1.
\end{align}Then, the relation (31) yields
 \begin{align}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}J_0(\vec{x},t) &\ge \textsf{P}
\bigg(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x},\Big|\frac{N^{\ast}(t)-\lambda t}{t}\Big|\le \varepsilon \bigg)
\nonumber\\
&\hspace{3.5cm}\cdot(\lfloor\lambda t-\varepsilon t\rfloor) \ldots (\lfloor\lambda t-\varepsilon t-m+1\rfloor) \prod_{i=1}^{m}\overline{F}_i(\nu x_i)
\nonumber\\
&\ge \bigg(\textsf{P}
\big(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x}\big)-\textsf{P}\big(\Big|\frac{N^{\ast}(t)-\lambda t}{t}\Big| \gt \varepsilon \big)\bigg)
\nonumber\\
&\hspace{3.5cm}\cdot(\lfloor\lambda t-\varepsilon t\rfloor) \ldots (\lfloor\lambda t-\varepsilon t-m+1\rfloor) \prod_{i=1}^{m}\overline{F}_i(\nu x_i).
\end{align}
\begin{align}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}J_0(\vec{x},t) &\ge \textsf{P}
\bigg(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x},\Big|\frac{N^{\ast}(t)-\lambda t}{t}\Big|\le \varepsilon \bigg)
\nonumber\\
&\hspace{3.5cm}\cdot(\lfloor\lambda t-\varepsilon t\rfloor) \ldots (\lfloor\lambda t-\varepsilon t-m+1\rfloor) \prod_{i=1}^{m}\overline{F}_i(\nu x_i)
\nonumber\\
&\ge \bigg(\textsf{P}
\big(\vec{S}_{\lfloor\lambda t-\varepsilon t\rfloor,(1,\ldots,m)}-\vec{\mu} \lambda t \gt ( 1-\nu ) \vec{x}\big)-\textsf{P}\big(\Big|\frac{N^{\ast}(t)-\lambda t}{t}\Big| \gt \varepsilon \big)\bigg)
\nonumber\\
&\hspace{3.5cm}\cdot(\lfloor\lambda t-\varepsilon t\rfloor) \ldots (\lfloor\lambda t-\varepsilon t-m+1\rfloor) \prod_{i=1}^{m}\overline{F}_i(\nu x_i).
\end{align} Hence, by the condition ![]() $F_i\in \mathcal{C}$ for
$F_i\in \mathcal{C}$ for ![]() $i\in\mathbb{I}$, we have
$i\in\mathbb{I}$, we have
 \begin{align}
\lim_{\varepsilon \downarrow 0} \lim_{\nu \downarrow 1} \liminf_{t\rightarrow \infty}\inf_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}J_0(\vec{x},t)}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}\ge 1,
\end{align}
\begin{align}
\lim_{\varepsilon \downarrow 0} \lim_{\nu \downarrow 1} \liminf_{t\rightarrow \infty}\inf_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}J_0(\vec{x},t)}{(\lambda t)^m\prod_{i=1}^{m}\overline{F}_i(x_i)}\ge 1,
\end{align} where the Lemma 3.1 and (32) are used. As for ![]() $J_1(\vec{x},t)$, by interchanging the order of summations, we have
$J_1(\vec{x},t)$, by interchanging the order of summations, we have
 \begin{align*}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) \le &\sum_{\substack{j_1\neq p_1,\\1\le j_1,\ldots,j_m, p_1\le\lfloor\lambda t+\varepsilon t\rfloor }}\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}{\textsf{P}(N(t)= n|X_{1 p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})}
\nonumber\\
&\hspace{4.5cm} \cdot\textsf{P}(X_{1p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})
\nonumber\\
&\le\sum_{\substack{j_1\neq p_1,\\1\le j_1,\ldots,j_m, p_1\le\lfloor\lambda t+\varepsilon t\rfloor }}\textsf{P}(X_{1 p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I}).
\end{align*}
\begin{align*}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) \le &\sum_{\substack{j_1\neq p_1,\\1\le j_1,\ldots,j_m, p_1\le\lfloor\lambda t+\varepsilon t\rfloor }}\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t}{\textsf{P}(N(t)= n|X_{1 p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})}
\nonumber\\
&\hspace{4.5cm} \cdot\textsf{P}(X_{1p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})
\nonumber\\
&\le\sum_{\substack{j_1\neq p_1,\\1\le j_1,\ldots,j_m, p_1\le\lfloor\lambda t+\varepsilon t\rfloor }}\textsf{P}(X_{1 p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I}).
\end{align*} By Assumption 2.1, the largest one of ![]() $\textsf{P}(X_{1p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})$ in the above display is
$\textsf{P}(X_{1p_1} \gt \nu x_1, X_{ij_i} \gt \nu x_i, i\in \mathbb{I})$ in the above display is  $\big(g(m)\big)^{\frac{(m+1)}{2}}\overline {F}_1(\nu x_1)\prod_{i=1}^{m}\overline {F}_i(\nu x_i)$. Hence,
$\big(g(m)\big)^{\frac{(m+1)}{2}}\overline {F}_1(\nu x_1)\prod_{i=1}^{m}\overline {F}_i(\nu x_i)$. Hence,
 \begin{align*}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) &\le\big(g(m)\big)^{\frac{(m+1)}{2}}(\lfloor\lambda t+\varepsilon t\rfloor)^{m+1}\overline {F}_1(\nu x_1)\prod_{i=1}^{m}\overline {F}_i(\nu x_i).
\end{align*}
\begin{align*}
\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) &\le\big(g(m)\big)^{\frac{(m+1)}{2}}(\lfloor\lambda t+\varepsilon t\rfloor)^{m+1}\overline {F}_1(\nu x_1)\prod_{i=1}^{m}\overline {F}_i(\nu x_i).
\end{align*} Then, by virtue of ![]() $\mu_1 \lt \infty$, we have
$\mu_1 \lt \infty$, we have  $t\overline{F}_1(\nu x_1)\le {\gamma}_{1}^{-1}{x_1}\overline{F}_1(\nu x_1)\rightarrow 0$, which implies that
$t\overline{F}_1(\nu x_1)\le {\gamma}_{1}^{-1}{x_1}\overline{F}_1(\nu x_1)\rightarrow 0$, which implies that
 \begin{align}
\lim_{\nu \downarrow 1}\limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) }{(\lambda t)^m\prod_{i=1}^{m}\overline {F}_i(\nu x_i)}=0.
\end{align}
\begin{align}
\lim_{\nu \downarrow 1}\limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_1(\vec{x},t) }{(\lambda t)^m\prod_{i=1}^{m}\overline {F}_i(\nu x_i)}=0.
\end{align}Similarly, we can show
 \begin{align}
\lim_{\nu \downarrow 1}\limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_s(\vec{x},t) }{(\lambda t)^m\prod_{i=1}^{m}\overline {F}_i(\nu x_i)}=0, s=2,\ldots,m.
\end{align}
\begin{align}
\lim_{\nu \downarrow 1}\limsup_{t\rightarrow \infty}\sup_{\vec{x}\ge \vec{\gamma }t}\frac{\sum_{\lambda t-\varepsilon t\le n\le \lambda t+\varepsilon t} J_s(\vec{x},t) }{(\lambda t)^m\prod_{i=1}^{m}\overline {F}_i(\nu x_i)}=0, s=2,\ldots,m.
\end{align}Hence, by combining (34)–(36), (23) follows, as desired, and the proof of Theorem 2.1 is completed.
Acknowledgments
The authors are very grateful to all the reviewers for their useful suggestions in improving this paper. In particular, according to the suggestions of members of the editorial board, the authors have strengthened the discussions on technical novelty in the introduction of the paper to make our contribution more transparent.
Funding statement
This work is supported by the National Natural Science Foundation of China (Nos. 12371150 and 11971432) and Zhejiang Provincial Natural Science Foundation of China (No. LY23A010001).
Competing interest
The authors declare that they have no competing interest.