Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T21:02:15.703Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPLICIT SOLUTIONS FOR CONTINUOUS-TIME QBD PROCESSES BY USING RELATIONS BETWEEN MATRIX GEOMETRIC ANALYSIS AND THE PROBABILITY GENERATING FUNCTIONS METHOD

Part of: Operations research and management science Computer system organization Special processes

Published online by Cambridge University Press:  03 January 2020

Gabi Hanukov Open the ORCID record for Gabi Hanukov [Opens in a new window]  and
Uri Yechiali
Gabi Hanukov
Affiliation:
Department of Management, Bar-Ilan University, Ramat Gan 5290002, Israel E-mail: [email protected]
Uri Yechiali
Affiliation:
Department of Statistics and Operations Research, School of Mathematical Sciences, Tel Aviv University, Tel Aviv 6997801, Israel E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two main methods are used to solve continuous-time quasi birth-and-death processes: matrix geometric (MG) and probability generating functions (PGFs). MG requires a numerical solution (via successive substitutions) of a matrix quadratic equation A0 + RA1 + R2A2 = 0. PGFs involve a row vector 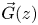$\vec{G}(z)$ of unknown generating functions satisfying 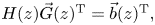$H(z)\vec{G}{(z)^\textrm{T}} = \vec{b}{(z)^\textrm{T}},$ where the row vector 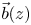$\vec{b}(z)$ contains unknown “boundary” probabilities calculated as functions of roots of the matrix H(z). We show that: (a) H(z) and 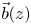$\vec{b}(z)$ can be explicitly expressed in terms of the triple A0, A1, and A2; (b) when each matrix of the triple is lower (or upper) triangular, then (i) R can be explicitly expressed in terms of roots of 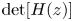$\det [H(z)]$; and (ii) the stability condition is readily extracted.

Keywords

continuous-time QBD processesprobability generating functionsmatrix geometriccalculation of the rate matrix R

MSC classification

Primary: 60K25: Queueing theory
Secondary: 68M20: Performance evaluation; queueing; scheduling 90B22: Queues and service
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 35 , Issue 3 , July 2021 , pp. 565 - 580
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Altman, E., Jiménez, T., Núñez Queija, R., & Yechiali, U. (2004). Optimal routing among · /M/1 queues with partial information. Stochastic Models 20(2): 149–171.CrossRefGoogle Scholar
2.Armony, M., Perel, E., Perel, N., & Yechiali, U. (2019). Exact analysis for multi-server queueing systems with cross selling. Annals of Operations Research 274(1–2): 75–100.CrossRefGoogle Scholar
3.Artalejo, J.R., & Gómez-Corral, A. (2008). Retrial queueing systems: A computational approach. Berlin, Heidelberg: Springer-Verlag.CrossRefGoogle Scholar
4.Bini, D.A., Latouche, G., & Meini, B. (2005). Numerical methods for structured Markov chains. Oxford University Press.CrossRefGoogle Scholar
5.Hanukov, G., Avinadav, T., Chernonog, T., Spiegel, U., & Yechiali, U. (2017). A queueing system with decomposed service and inventoried preliminary services. Applied Mathematical Modeling 47: 276–293.CrossRefGoogle Scholar
6.Hanukov, G., Avinadav, T., Chernonog, T., Spiegel, U., & Yechiali, U. (2018). Improving efficiency in service systems by performing and storing “preliminary services”. International Journal of Production Economics 197: 174–185.CrossRefGoogle Scholar
7.Hanukov, G., Avinadav, T., Chernonog, T., & Yechiali, U. (2019). Performance improvement of a service system via stocking perishable preliminary services. European Journal of Operational Research 274(3): 1000–1011.CrossRefGoogle Scholar
8.Haviv, M. (2013). A Course in Queueing Theory.CrossRefGoogle Scholar
9.Jolles, A., Perel, E., & Yechiali, U. (2018). Alternating server with non-zero switch-over times and opposite-queue threshold-based switching policy. Performance Evaluation 126: 22–38.CrossRefGoogle Scholar
10.Kapodistria, S., & Palmowski, Z. (2017). Matrix geometric approach for random walks: Stability condition and equilibrium distribution. Stochastic Models 33(4): 572–597.CrossRefGoogle Scholar
11.Latouche, G., & Ramaswami, V. (1999) Introduction to matrix analytic methods in stochastic modeling. Philadelphia, PA: ASA-SIAM Series on Statistics and Applied Probability, SIAM.CrossRefGoogle Scholar
12.Levy, Y., & Yechiali, U. (1976). An M/M/s queue with servers’ vacations. INFOR: Information Systems and Operational Research 14(2): 153–163.Google Scholar
13.Neuts, M. (1981). Matrix-geometric solutions in stochastic models: An algorithmic approach. Baltimore, MD: Johns Hopkins University Press.Google Scholar
14.Paz, N., & Yechiali, U. (2014). An M/M/1 queue in random environment with disasters. Asia-Pacific Journal of Operational Research 31(3): 1450016.CrossRefGoogle Scholar
15.Perel, E., & Yechiali, U. (2008). Queues where customers of one queue act as servers of the other queue. Queueing Systems 60(3–4): 271–288.CrossRefGoogle Scholar
16.Perel, N., & Yechiali, U. (2013). The Israeli queue with priorities. Stochastic Models 29(3): 353–379.CrossRefGoogle Scholar
17.Perel, N., & Yechiali, U. (2014). The Israeli queue with infinite number of groups. Probability in the Engineering and Informational Sciences 28(1): 1–19.CrossRefGoogle Scholar
18.Perel, E., & Yechiali, U. (2017). Two-queue polling systems with switching policy based on the queue that is not being served. Stochastic Models 33(3): 430–450.CrossRefGoogle Scholar
19.Phung-Duc, T. (2017). Exact solutions for M/M/c/setup queues. Telecommunication Systems 64(2): 309–324.CrossRefGoogle Scholar
20.Van Leeuwaarden, J.S.H., & Winands, E.M.M. (2006). Quasi-birth-and-death processes with an explicit rate matrix. Stochastic Models 22(1): 77–98.CrossRefGoogle Scholar
21.Van Houdt, B., & van Leeuwaarden, J.S.H. (2011). Triangular M/G/1-type and tree-like quasi-birth-death Markov chains. INFORMS Journal on Computing 23(1): 165–171.CrossRefGoogle Scholar
22.Van Leeuwaarden, J.S.H., Squillante, M.S., & Winands, E.M. (2009). Quasi-birth-and-death processes, lattice path counting, and hypergeometric functions. Journal of Applied Probability 46(2): 507–520.CrossRefGoogle Scholar