Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T06:25:09.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Customer Scheduling with Incomplete Information

Published online by Cambridge University Press:  27 July 2009

Ulrich Rieder  and
Jürgen Weishaupt
Ulrich Rieder
Affiliation:
Department of Mathematics, University of Ulm, 89069 Ulm, Germany
Jürgen Weishaupt
Affiliation:
Department of Mathematics, University of Ulm, 89069 Ulm, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

A stochastic scheduling model with linear waiting costs and unknown routing probabilities is considered. Using a Bayesian approach and methods of Bayesian dynamic programming, we investigate the finite-horizon stochastic scheduling problem with incomplete information. In particular, we study an equivalent nonstationary bandit model and show the monotonicity of the total expected reward and of the Gittins index. We derive the monotonicity and well-known structural properties of the (greatest) maximizers, the so-called stay-on-a-winnerproperty and the stopping-property. The monotonicity results are based on a special partial ordering on .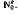

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 9 , Issue 2 , April 1995 , pp. 269 - 284
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baras, J.S., Dorsey, A.J. & Makowski, A.M. (1985). Two competing queues with linear costs and geometric service requirements: The μc-rule is often optimal. Advances in Applied Probability 17: 186–209.CrossRefGoogle Scholar
2.Berry, D.A. & Fristedt, B. (1985). Bandit problems. London: Chapman & Hall.CrossRefGoogle Scholar
3.Burnetas, A.P. & Katehakis, M.N. (1993). On sequencing two types of tasks on a single processor under incomplete information. Probability in the Engineering and Informational Sciences 7: 85–119.CrossRefGoogle Scholar
4.Buyukkoc, C., Varaiya, P. & Walrand, J. (1985). The cμ rule revisited. Advances in Applied Probability 17: 237–238.CrossRefGoogle Scholar
5.Gittins, J.C. (1989). Multi-armed bandit allocation indices. Chichester: Wiley.Google Scholar
6.Gittins, J.C. & Glazebrook, K.D. (1977). On Bayesian models in stochastic scheduling. Journal of Applied Probability 14: 556–565.CrossRefGoogle Scholar
7.Glazebrook, K.D. (1978). On the optimal allocation of two or more treatments in a controlled clinical trial. Biometrika 65: 335–340.CrossRefGoogle Scholar
8.Rieder, U. (1975). Bayesian dynamic programming. Advances in Applied Probability 7: 330–348.CrossRefGoogle Scholar
9.Rieder, U. (1988). Bayessche Kontrollmodelle. Skript, Universität Ulm.Google Scholar
10.Rieder, U. & Wagner, H. (1991). Structured policies in the sequential design of experiments. Annals of Operations Research 32: 165–188.CrossRefGoogle Scholar
11.Ross, S.M. (1983). Introduction to stochastic dynamic programming. New York: Academic Press.Google Scholar
12.Tcha, D.W. & Pliska, S.R. (1977). Optimal control of single server queueing networks and multiclass M/G/l queues with feedback. Operations Research 25: 248–258.CrossRefGoogle Scholar
13.Weishaupt, J. (1992). Optimalitatsaussagen für stochastische Schedulingprobleme. Dissertation, Universität Ulm.Google Scholar
14.Weishaupt, J. (1994). Optimal myopic policies and index policies for stochastic scheduling problems. ZOR — Mathematical Methods of Operations Research 40: 75–89.CrossRefGoogle Scholar