Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T07:38:22.120Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC BEHAVIOR OF EXTREMAL EVENTS FOR AGGREGATE DEPENDENT RANDOM VARIABLES

Published online by Cambridge University Press:  13 August 2013

Die Chen ,
Tiantian Mao  and
Taizhong Hu
Die Chen
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China; Department of School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China E-mail: [email protected]
Tiantian Mao
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China E-mails: [email protected]; [email protected]
Taizhong Hu
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, Anhui 230026, China E-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a portfolio of n identically distributed risks X1, …, Xn with dependence structure modelled by an Archimedean survival copula. It is known that the probability of a large aggregate loss of 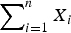$\sum\nolimits_{i=1}^{n} X_{i}$ is in proportion to the probability of a large individual loss of X1. The proportionality factor depends on the dependence strength and the tail behavior of the individual risk. In this paper, we establish analogous results for an aggregate loss of the form g(X1, …, Xn) under the more general model in which the Xi's have different but tail-equivalent distributions and the copula remains unchanged, where g is a homogeneous function of order 1. Properties of these factors are studied, and asymptotic Value-at-Risk behaviors of functions of dependent risks are also given. The main results generalize those in Wüthrich [16], Alink, Löwe, and Wüthrich [2], Barbe, Fougères, and Genest [4], and Embrechts, Nešlehová, and Wüthrich [9].

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 27 , Issue 4 , October 2013 , pp. 507 - 531
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alink, S. (2007). Copulas and extreme values. PhD thesis, Radboud University Nijmegen.Google Scholar
2.Alink, S., Löwe, M., & Wüthrich, M.V. (2004). Diversification of aggregate dependent risks. Insurance: Mathematics and Economics 35: 77–95.Google Scholar
3.Alink, S., Löwe, M., & Wüthrich, M.V. (2007). Diversification for general copula dependence. Statistica Neerlandica 61: 446–465.CrossRefGoogle Scholar
4.Barbe, P., Fougères, A.-L., & Genest, C. (2006). On the tail behavior of sums of dependent risks. Astin Bulletin 36: 361–373.CrossRefGoogle Scholar
5.Bingham, N.H., Goldie, C.M., & Teugels, J.L. (1987). Regular variation. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
6.Chen, D., Mao, T., Pan, X., & Hu, T. (2012). Extreme value behavior of aggregate dependent risks. Insurance: Mathematics and Economics 50: 99–108.Google Scholar
7.de Haan, L. & Ferreira, A. (2006). Extreme value theory. Springer Series in Operations Research and Financial Engineering. New York: Springer.CrossRefGoogle Scholar
8.Embrechts, P., Klüppelberg, C., & Mikosch, T. (1997). Modelling extremal events for finance and insurance. Berlin: Springer-Verlag.CrossRefGoogle Scholar
9.Embrechts, P., Nešlehová, J., & Wüthrich, M.V. (2009). Additivity properties for value-at-risk under Archimedean dependence and heavy-tailedness. Insurance: Mathematics and Economics 44: 164–169.Google Scholar
10.Joe, H. (1997). Multivariate models and dependence concepts. London: Chapman & Hall.Google Scholar
11.McNeil, A.J. & Nešlehová, J. (2009). Multivariate Archimedean copulas, d-monotone functions and ℓ1-norm symmetric distributions. Annals of Statistics 37: 3059–3097.CrossRefGoogle Scholar
12.Müller, A. & Stoyan, D. (2002). Comparison methods for stochastic models and risks. West Sussex: John Wiley & Sons, Ltd.Google Scholar
13.Nelsen, R.B. (2006). An introduction to copulas 2nd ed.New York: Springer.Google Scholar
14.Resnick, S.I. (2007). Heavy-tail phenomena. Springer Series in Operations Research and Financial Engineering, New York: Springer.Google Scholar
15.Shaked, M. & Shanthikumar, J.G. (2007). Stochastic orders. New York: Springer.CrossRefGoogle Scholar
16.Wüthrich, M.V. (2003). Asymptotic value-at-risk estimates for sums of dependent random variables. Astin Bulletin 33: 75–92.CrossRefGoogle Scholar