Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T07:11:04.706Z Has data issue: false hasContentIssue false
  • English
  • Français

A closed-form pricing formula for catastrophe equity options

Published online by Cambridge University Press:  15 July 2021

Puneet Pasricha Open the ORCID record for Puneet Pasricha [Opens in a new window] ,
Anubha Goel Open the ORCID record for Anubha Goel [Opens in a new window]  and
Song-Ping Zhu
Puneet Pasricha
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia. E-mails: [email protected], [email protected]
Anubha Goel
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi 110016, India. E-mail: [email protected]
Song-Ping Zhu
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, NSW 2522, Australia. E-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we derive a closed-form pricing formula for catastrophe equity put options under a stochastic interest rate framework. A distinguishing feature of the proposed solution is its simplified form in contrast to several recently published formulae that require evaluating several layers of infinite sums of 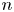$n$-fold convoluted distribution functions. As an application of the proposed formula, we consider two different frameworks and obtain the closed-form formula for the joint characteristic function of the asset price and the losses, which is the only required ingredient in our pricing formula. The prices obtained by the newly derived formula are compared with those obtained using Monte-Carlo simulations to show the accuracy of our formula.

Keywords

Catastrophe put optionJoint characteristic functionJump-diffusionStochastic interest rate
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1103 - 1115
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carr, P. & Madan, D. (1999). Option valuation using the fast Fourier transform. Journal of Computational Finance 2(4): 61–73.CrossRefGoogle Scholar
Chang, L.-f. & Hung, M.-w. (2009). Analytical valuation of catastrophe equity options with negative exponential jumps. Insurance: Mathematics and Economics 44(1): 59–69.Google Scholar
Chang, C.-C., Lin, S.-K., & Yu, M.-T. (2011). Valuation of catastrophe equity puts with Markov-modulated Poisson processes. Journal of Risk and Insurance 78(2): 447–473.CrossRefGoogle Scholar
Cox, S.H., Fairchild, J.R., & Pedersen, H.W. (2004). Valuation of structured risk management products. Insurance: Mathematics and Economics 34(2): 259–272.Google Scholar
Griebsch, S.A. & Wystup, U. (2011). On the valuation of fader and discrete barrier options in Heston's stochastic volatility model. Quantitative Finance 11(5): 693–709.CrossRefGoogle Scholar
Heston, S.L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies 6(2): 327–343.CrossRefGoogle Scholar
Huang, J., Zhu, W., & Ruan, X. (2014). Option pricing using the fast Fourier transform under the double exponential jump model with stochastic volatility and stochastic intensity. Journal of Computational and Applied Mathematics 263: 152–159.CrossRefGoogle Scholar
Hull, J. & White, A. (1993). One-factor interest-rate models and the valuation of interest-rate derivative securities. Journal of Financial and Quantitative Analysis 28(2): 235–254.CrossRefGoogle Scholar
Jaimungal, S. & Wang, T. (2006). Catastrophe options with stochastic interest rates and compound Poisson losses. Insurance: Mathematics and Economics 38(3): 469–483.Google Scholar
Kim, H.-S., Kim, B., & Kim, J. (2014). Pricing perpetual American CatEPut options when stock prices are correlated with catastrophe losses. Economic Modelling 41: 15–22.CrossRefGoogle Scholar
Lin, X.S. & Wang, T. (2009). Pricing perpetual American catastrophe put options: a penalty function approach. Insurance: Mathematics and Economics 44(2): 287–295.Google Scholar
Shephard, N.G. (1991). From characteristic function to distribution function: a simple framework for the theory. Econometric Theory 7(4): 519–529.CrossRefGoogle Scholar
Vasicek, O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics 5(2): 177–188.CrossRefGoogle Scholar
Wang, X. (2016). Catastrophe equity put options with target variance. Insurance: Mathematics and Economics 71: 79–86.Google Scholar
Yu, J. (2015). Catastrophe options with double compound Poisson processes. Economic Modelling 50: 291–297.CrossRefGoogle Scholar