Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T00:19:04.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Product Gaussian Quadrature on Circular Lunes

Published online by Cambridge University Press:  28 May 2015

Gaspare Da Fies  and
Marco Vianello
Gaspare Da Fies
Affiliation:
Department of Mathematics, University of Padova, Italy
Marco Vianello*
Affiliation:
Department of Mathematics, University of Padova, Italy
*
*Corresponding author.Email address:[email protected]
Get access

Abstract

Resorting to recent results on subperiodic trigonometric quadrature, we provide three product Gaussian quadrature formulas exact on algebraic polynomials of degree n on circular lunes. The first works on any lune, and has 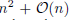cardinality. The other two have restrictions on the lune angular intervals, but their cardinality is

Keywords

65D32Product Gaussian quadraturesubperiodic trigonometric quadraturecircular lunes
Type
Research Article
Information
Numerical Mathematics: Theory, Methods and Applications , Volume 7 , Issue 2 , May 2014 , pp. 251 - 264
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bauman, B. and Xiao, H., Gaussian quadrature for optical design with noncircular pupils and fields, and broad wavelength range, Proc. SPIE 7652(2) (2010), 1–12.Google Scholar
[2] Bos, L. and Vianello, M., Subperiodic trigonometric interpolation and quadrature, Appl. Math. Comput. 218 (2012), 10630–10638.Google Scholar
[3] Da Fies, G., Sommariva, A. and Vianello, M., Algebraic cubature by linear blending of elliptical arcs, Appl. Numer. Math. 74 (2013), 49–61.CrossRefGoogle Scholar
[4] Da Fies, G. and Vianello, M., Algebraic cubature on planar lenses and bubbles, Dolomites Res. Notes Approx. 5 (2012), 7–12.Google Scholar
[5] Da Fies, G. and Vianello, M., Trigonometric Gaussian quadrature on subintervals of the period, Electron. Trans. Numer. Anal. 39 (2012), 102–112.Google Scholar
[6] Da Fies, G. and Vianello, M., On the Lebesgue constant of subperiodic trigonometric interpolation, J. Approx>. Theory 167 (2013), 59–64.Google Scholar
[7] Da Fies, G., Sommariva, A. and Vianello, M., Matlab functions for subperiodic trigonometric quadrature and for product Gaussian quadrature on circular sections, online at: http://www.math.unipd.it/∼marcov/CAAsoft.html.Google Scholar
[8] Gautschi, W., Orthogonal Polynomials: Computation and Approximation, Oxford University Press, New York, 2004.Google Scholar
[9] Gautschi, W., Orthogonal polynomials (in Matlab), J. Comput. Appl. Math. 178 (2005), 215–234, software online at: http://www.cs.purdue.edu/archives/2002/wxg/codes.Google Scholar
[10] Gautschi, W., Sub-range Jacobi polynomials, Numer. Algorithms 61 (2012), 649–657.Google Scholar
[11] Langton, S.G., The quadrature of lunes, from Hippocrates to Euler, Euler at 300, 5362, MAA Spectrum, Math. Assoc. America, Washington, DC, 2007.Google Scholar
[12] Meurant, G. and Sommariva, A., Fast variants of the Golub and Welsch algorithm for symmetric weight functions in Matlab, Numer. Algorithms, published online 23 November 2013.Google Scholar
[13] Pleśniak, W., Multivariate polynomial inequalities via pluripotential theory and subanalytic geometry methods, Banach Center Publ. 72 (2006), 251–261.CrossRefGoogle Scholar
[14] Pleśniak, W., Multivariate Jackson Inequality, J. Comput. Appl. Math. 233 (2009), 815–820.Google Scholar
[15] Postnikov, M.M., The problem of squarable lunes, American Mathematical Monthly 107 (2000), 645–651 (translated from the Russian by Abe Shenitzer).Google Scholar
[16] Santin, G., Sommariva, A. and Vianello, M., An algebraic cubature formula on curvilinear polygons, Appl. Math. Comput. 217 (2011), 10003–10015.Google Scholar
[17] Sommariva, A. and Vianello, M., Gauss-Green cubature and moment computation over arbitrary geometries, J. Comput. Appl. Math. 231 (2009), 886–896.Google Scholar
[18] Stasica, J., The Whitney condition for subanalytic sets, Zeszyty Nauk. Uniw. Jagiellon. Prace Mat. 23 (1982), 211–221.Google Scholar