Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-14T10:52:49.262Z Has data issue: false hasContentIssue false
  • English
  • Français

Zum Begriff der Borelmessbarkeit

Published online by Cambridge University Press:  22 January 2016

Robert Zobel
Robert Zobel*
Affiliation:
Universität Braunschweig
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In dieser Arbeit werden die Voraussetzungen untersucht, die an einen topologischen Raum (X, 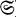) mit dem System offener Mengen 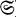zu stellen sind, damit einige der in der Literatur geläufigen Begriffe der Borelmeβbarkeit reellwertiger Funktionen äquivalent sind.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 78 , May 1980 , pp. 57 - 63
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1980

References

Literatur

[1] Bourbaki, N., Eléments de mathématique. Intégration Livre XIII, Chap. IV, Hermann, Paris.Google Scholar
[2] Courrège, P., Théorie de la mesure. Centre de Documentation Universtiaire, Paris (1962).Google Scholar
[3] Est, W. T. van and Freudenthal, H., Trennung durch stetige Funktionen in topologischen Räumen. Indagationes Math. 13 (1951), 359–368.Google Scholar
[4] Kölzow, D., Differentiation von Maβen, Lecture Notes in Mathematics 65, Springer, Berlin (1968).Google Scholar
[5] Segal, I. E., Equivalence of measure spaces, Amer. J. Math. 73 (1951), 275–313.Google Scholar
[6] Stones, M. H., The generalized Weierstrass approximation theorem, Math. Mag. ‘21 (1947/48), 237–254.Google Scholar
[7] Wage, M. L., A generalization of Lusin’s theorem, Proc. Amer. Math. Soc. 52 (1975), 327–332.Google Scholar