Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-07T23:18:19.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique Continuation for Parabolic Equations of Higher Order

Published online by Cambridge University Press:  22 January 2016

Lu-San Chen  and
Tadashi Kuroda
Lu-San Chen
Affiliation:
Department of Mathematics, Taiwan provincial Cheng-Kung University, Tainan and Mathematical Institute, Nagoya University, Nagoya
Tadashi Kuroda
Affiliation:
Department of Mathematics, Taiwan provincial Cheng-Kung University, Tainan and Mathematical Institute, Nagoya University, Nagoya
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let x = (xl,…xn) be a point in the n-dimensional Euclidean space and let 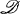be the unit sphere 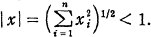In the (n + 1)-dimensional Euclidean space with coordinate (x, t), we put

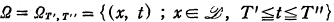
and

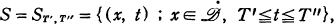
where 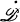denotes the boundary of 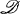. We also use the following notation:

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 26 , February 1966 , pp. 115 - 120
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Edmunds, D. E.: Two uniqueness theorems associated with parabolic differential operators, Journ. London Math. Soc., 39 (1964), 345–354.Google Scholar
[2] Gårding, A.: Dirichlet’s problem for linear elliptic partial differential equation, Math, Scand., 1 (1953), 55–72.CrossRefGoogle Scholar
[3] Ito, S. and Yamabe, H.: A unique continuation theorem for solutions of a parabolic equation, Journ. Math. Soc. Jap., 10 (1958), 314–321.Google Scholar
[4] Lees, M.: Asymptotic behaviour of solutions of parabolic differential inequalities, Canad. Journ. Math., 14 (1962), 626–631.Google Scholar
[5] Lees, M. and Protter, M. H.: Unique continuation for parabolic differential equations and inequalities, Duke Math. Journ., 28 (1961), 369–382.Google Scholar
[6] Lions, J. L. and Malgrange, B.: Sur l’unicité rétrograde dans les problemes mixtes paraboliques, Math. Scand., 8 (1960), 277–286.CrossRefGoogle Scholar
[7] Mizohata, S.: Unicité du prolongement des solutions pour quelques opérateurs différentiels paraboliques, Mem. Coll. Sci., Univ. Kyoto, A 31 (1958), 219–239.Google Scholar
[8] Nirenberg, L.: Remarks on strongly elliptic partial differential equations, Comm. Pure Appl. Math., 8 (1955), 648–674.Google Scholar
[9] Protter, M. H.: Properties of solutions of parabolic equations and inequalities, Canad. Journ. Math., 13 (1961), 331–345.CrossRefGoogle Scholar
[10] Yamabe, H.: A unique continuation theorem of a diffusion equation, Ann. of Math., 69 (1959), 462–466.CrossRefGoogle Scholar
[11] Yosida, K.: An abstract analyticity in time for solutions of a diffusion equation, Proc. Jap. Acad., 35 (1959), 109–113.Google Scholar