Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-03T09:08:10.768Z Has data issue: false hasContentIssue false
  • English
  • Français

A Property of Some Poincaré Theta-Series

Published online by Cambridge University Press:  22 January 2016

Tohru Akaza
Tohru Akaza*
Affiliation:
Mathematical Institute, Kanazawa University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider circles cν(ν = ±1, ±2, …) with centers ξν on the real axis of the z-plane such that they are disjoint from each other and cluster to infinity z = ∞ from the both sides of the real axis. Here, without loss of generality, we may assume that 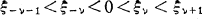for every positive integer ν.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 16 , February 1960 , pp. 189 - 194
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1960

References

[1] Burnside, W., On a class of automorphic functions, Proc. London Math. Soc., 23 (1891), 49–88.Google Scholar
[2] Myrberg, L., Normalintegral auf zweiblättrigen Riemannschen Flächen mit reelen Verzweigungspunkten, Ann. Acad. Sci. Fenn., A-I, 71 (1950), 1–50.Google Scholar
[3] Myrberg, P. J., Über analytische Funktionen auf transzendenten zweiblättrigen Riemannschen Flächen mit reelen Verzweigungspunkten, Acta Math., 76 (1944), 184–224.Google Scholar
[4] Myrberg, P. J., Über Integrale auf transzendenten symmetrischen Riemannschen Flachen, Ann. Acad. Sci. Fenn., A-I, 31 (1945), 1–20.Google Scholar
[5] Myrberg, P. J., Über analytische Funktionen auf transzendenten Riemannschen Flächen, X. Congr. Math. Scand., Copenhagen, (1946), 77–96.Google Scholar