Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T23:42:21.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial regularity and applications

Published online by Cambridge University Press:  22 January 2016

Tadato Matsuzawa
Tadato Matsuzawa*
Affiliation:
Department of Mathematics, Faculty of Science, Nagoya University, Chikusa-ku, Nagoya 464, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem to determine the Gevrey index of solutions of a given hypoelliptic partial differential equation seems to be not yet well investigated. In this paper, we shall show the Gevrey indices of solutions of the equations of Grushin type, [6], are determined by a rather simple application of a straightforward extension of the results given in [7], [8] and [13]. For simplicity to construct left parametrices in the operator valued sense, we shall consider the equations under the stronger condition than that of [6] (cf. Condition 1 of Section 3). Typical examples of Grushin type are given by 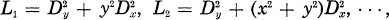which will be discussed in Section 4. We remark that our approach may be compared with the one to a similar problem discussed in [17] by using suitable L2-estimates constructed in [16].

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 103 , October 1986 , pp. 133 - 143
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[1] Baouendi, M. S. and Goulaouic, C., Nonanalytic hypoellipticity for some degenerate elliptic operators, Bull. Amer. Math. Soc, 78, No. 3 (1972), 483–486.Google Scholar
[2] Beals, R., Spatially inhomogeneous pseudodifferential operators, II, Comm. Pure Appl. Math., XXVII, (1974), 161–205.Google Scholar
[3] Croc, E., Dermenjian, Y. et Iftimie, V., Une classe d’ opérateurs pseudodifferentiels partiellement hypoelliptique-analytiques, J. Math, pures et appi., 57 (1978), 255–278.Google Scholar
[4] Friberg, J., Estimates for partially hypoelliptic differential operators, Comm. Mem. math. Univ. Lund, 17 (1963), 1–97.Google Scholar
[5] Gârdng, L. et Malgrange, B., Opérateurs différentiels partiellement hypoelliptiques et partiellement elliptiques, Mat. Scand., 9 (1961), 5–21.CrossRefGoogle Scholar
[6] Grushin, V. V., Hypoelliptic differential equations and pseudodifferential operators with operator valued symbols, Math. USSR Sbornik, 17 (1972), 497–514.Google Scholar
[7] Hashimoto, S., Matsuzawa, T. et Morimoto, Y., Opérateurs pseudodifférentiels et classes de Gevrey, Comm. in Partial Diff. Eqs., 8 (12), (1983), 1277–1289.Google Scholar
[8] Hashimoto, Y. and Matsuzawa, T., On a class of degenerate elliptic equations, Nagoya Math. J., 55 (1974), 181–204.Google Scholar
[9] Hörmander, L., On the theory of general partial differential operators, Acta Math., 94 (1955), 161–248.Google Scholar
[10] Hörmander, L., Pseudodifferential operators and hypoelliptic equations, Proc. Symp. Pure Math., 83 (1966), 129–209.Google Scholar
[11] Hörmander, L., Uniqueness theorems and wave front sets for solutions of linear differential equations with analytic coefficients, Comm. Pure Appl. Math., 24 (1971), 671–704.Google Scholar
[12] Matsuzawa, T., Opérateurs pseudodifférentiels et classes de Gevrey, Journées “Eqs aux Dér. parts.”, Saint-Jean-de-Monts (1982).Google Scholar
[13] Matsuzawa, T., Partially hypoelliptic pseudodifferential operators, Comm. in Partial Diff. Eqs., 9(11), (1984), 1059–1084.Google Scholar
[14] Métivier, G., Non hypoellipticité analytique pour C. R. Acad. Sc, 292 (1981), 401–404.Google Scholar
[15] Okaji, T., On the Gevrey index for some hypoelliptic operators, to appear.Google Scholar
[16] Parenti, C. and Rodino, L., Parametrices for a class of pseudodifferential operators, I, II, Annali Mat. Pura ed Appl., 125 (1980), 221–278.Google Scholar
[17] Rodino, L., Gevrey hypoellipticity for a class of operators with multiple characteristics, Astérisque, 89–90 (1981), 249–262.Google Scholar
[18] Treves, F., Introduction to pseudodifferential and Fourier integral operators, Vol. 1, Plenum Press (1981).Google Scholar