Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-14T22:00:52.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal control of ultimately bounded stochastic processes

Published online by Cambridge University Press:  22 January 2016

Yoshio Miyahara
Yoshio Miyahara*
Affiliation:
Shizuoka University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall consider the optimal control for a system governed by a stochastic differential equation

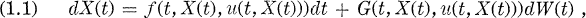
where u(t, x) is an admissible control and W(t) is a standard Wiener process. By an optimal control we mean a control which minimizes the cost and in addition makes the corresponding Markov process stable.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 53 , May 1974 , pp. 157 - 170
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1974

References

[1] Haussmann, U. G.; Optimal Stationary Control with State and Control Dependent Noise, SIAM J. Control, Vol. 9 No. 2 (1971) pp. 184–198.CrossRefGoogle Scholar
[2] Miyahara, Y.; Ultimate Boundedness of the Systems Governed by Stochastic Differential Equations, Nagoya Math. J. Vol. 47 (1972), pp. 111–144.Google Scholar
[3] Miyahara, Y.; Invariant Measures of Ultimately Bounded Stochastic Process, Nagoya Math. J. Vol. 49 (1973) pp. 149–153.CrossRefGoogle Scholar
[4] Wonham, W. M.; Optimal Stationary Control of a Linear System with State-dependent Noise, SIAM J. Control, Vol. 5, No. 3 (1967).CrossRefGoogle Scholar
[5] Wonham, W. M.; On Pole assignment in Multi-input Controllable linear systems, IEEE Trans. Automatic Control, AC-12 (1967), pp. 660–665.Google Scholar