Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bank, Steven B.
1972.
On solutions of algebraic differential equations whose coefficients are analytic functions in the unit disk.
Annali di Matematica Pura ed Applicata,
Vol. 92,
Issue. 1,
Bank, Steven B.
1973.
On Determining the Growth of Meromorphic Solutions of Algebraic Differential Equations Having Arbitrary Entire Coefficients.
Nagoya Mathematical Journal,
Vol. 49,
Issue. ,
p.
53.
Gol'dberg, A. A.
1975.
Meromorphic functions.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 2,
p.
157.
1993.
Nevanlinna Theory and Complex Differential Equations.
p.
311.
Kaufman, Robert
and
Langley, Jim
1997.
Steven barry bank 1939–1994.
Complex Variables, Theory and Application: An International Journal,
Vol. 34,
Issue. 1-2,
p.
1.


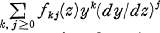 is a polynomial in
is a polynomial in 