Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-03T08:49:43.912Z Has data issue: false hasContentIssue false
  • English
  • Français

On Algebraic Groups Defined by Norm Forms of Separable Extensions

Published online by Cambridge University Press:  22 January 2016

Takashi Ono
Takashi Ono*
Affiliation:
Mathematical Institute Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be any field, and L a separable extension of K of finite degree. L has a structure of vector space over K, and we shall denote this space by V. The space of endomorphisms of V will be denoted by 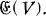Let x be any element of L, and N(x) the norm of x relative to the extension L/K. N is then a function defined on V with values in K. We shall call N the norm form on V. The multiplicative groups of non-zero elements of K and L will be denoted by K* and L* respectively. Let H be any subgroup of if K*. Then the elements z of L* such that N(z)∈H form a subgroup of L*, which we shall denote by GH. On the other hand the elements s of 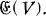such that N(sx) = Λ(s)N(x) with Λ(s)∈H for all X∈V, form obviously a subgroup of GL(V), which we shall denote by becomes an algebraic group if H=K* or {1}. In case 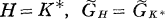will mean the group of linear transformations of V leaving semi-invariant the norm form of L/K and in case 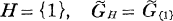will mean the group of linear transformations of V leaving invariant the norm form of L/K.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 11 , February 1957 , pp. 125 - 130
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1957

References

1) For definition, see p. 127, footnote 3).

2) Théorie des groupes de Lie: Vol. 2, Hermann, Paris, 1951, p. 170. We shall quote this book as C. II. We shall also quote Vol. 3 (1955) of the series as C. III.

3) We say that a group G is a semi-direct product of a normal subgroup N and a subgroup H if we have G = N·H and N∩H={e}, e being the identity in G. We see that μ(GH) is normal in ĞH by the relation σμ(z)<-1 = μ(<(z)),

4) Cf. C. III. Chap. VI §1.

5) C. II. Chap. II. §6. Prop. 8. If the characteristic of K is zero, we get dim K.μ(G) = n-1 by C. II. Chap. II. §14. Théorème 12.

6) C. II. Chap. II. §5. Prop. 4, §7. Prop. 2. Cor. 1.

7) Nm means the extension of N to VM . It is also the norm of the algebra LM over M with respect to the regular representation.

8) C. II. Chap. II. §6. Prop. 8. Cor.

9) C. III. Chap. VI. §1 Prop. 14.

10) C.f. C. II. Chap. II. §6. p. 119.

11) C.f. Dickson, Linear Groups, pp. 77-83.