Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-14T10:36:17.274Z Has data issue: false hasContentIssue false
  • English
  • Français

Microscopic asymptotics for solutions of some semilinear Elliptic equations

Published online by Cambridge University Press:  22 January 2016

Takayoshi Ogawa  and
Takashi Suzuki
Takayoshi Ogawa
Affiliation:
Graduate School of Polymathematics, Nagoya University, Furôchô, Chikusa-ku, Nagoya, 464-01, Japan
Takashi Suzuki
Affiliation:
Department of Mathematics, Osaka University, Machikaneyamachô, Toyonaka, Osaka 560, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In our previous work [8], we picked up the elliptic equation

(1)

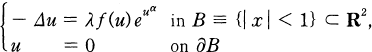
with the nonlinearity f(u) ⊇ 0 in C1. We studied the asymptotics of the family {(λ, u(x))} of classical solutions satisfying

(2)

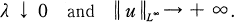
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 138 , June 1995 , pp. 33 - 50
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Adimurthi, , Existence of positive solutions of the semilinear Dirichlet problem with critical growth for the w-Laplacian, Ann. Scou. Norm. Sup. Pisa, 17 (1990), 393–413.Google Scholar
[ 2 ] Atkinson, F. V., Peletier, L. A., Ground states of — Δu = f(u) and the Emden-Fowler equation, Arch. Rat. Mech. Anal., 96 (1986), 147–165.Google Scholar
[ 3 ] Brezis, H., Merle, F., Uniform estimates and blow-up behavior for solutions of — Δu = V(x)eu in two dimensions, Comm. in Partial Differential Equations, 16 (1991), 1223–1253.Google Scholar
[ 4 ] Carleson, L., Chang, S-Y. A., On the existence of an extremal function for an inequality of J. Moser, Bull. Sc. Math., 110 (1986), 113–127.Google Scholar
[ 5 ] Gidas, B., Ni, W-M., Nirenberg, L., Symmetry and related properties via the maximum principle, Comm. Math. Phys., 68 (1979), 209–243.Google Scholar
[ 6 ] McLeod, J. B., Peletier, L. A., Observation on Moser’s inequality, Arch. Rat. Mech. Anal., 106 (1989), 261–285.Google Scholar
[ 7 ] Moser, J., A sharp form of an inequality by Trudinger, N., Indiana Univ. Math. J., 11 (1971), 1077–1092.CrossRefGoogle Scholar
[ 8 ] Ogawa, T., Suzuki, T., Nonlinear elliptic equations with critical growth related to the Trudinger inequality, to appear in Asymptotic Analysis.Google Scholar
[ 9 ] Shaw, M. C, Eigenfunctions of the nonlinear equation in R2 , Pacific J. Math., 129 (1987), 349–356.Google Scholar
[10] Struwe, M., Critical points of into Orlicz spaces, Ann. Inst. H. Poincaré Analyse non linéaire, 5 (1988), 425–464.Google Scholar
[11] Trudinger, N., On imbedding into Orlicz space and some applications, J. Math. Mech., 17 (1967), 473–484.Google Scholar