Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T12:44:58.488Z Has data issue: false hasContentIssue false
  • English
  • Français

The first line of the Bockstein spectral sequence on a monochromatic spectrum at an odd prime

Published online by Cambridge University Press:  11 January 2016

Ryo Kato  and
Katsumi Shimomura
Ryo Kato
Affiliation:
Graduate school of Mathematics, Nagoya University, Aichi, 464-8601, Japan, [email protected]
Katsumi Shimomura
Affiliation:
Department of Mathematics, Faculty of Science, Kochi University, Kochi, 780-8520, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The chromatic spectral sequence was introduced by Miller, Ravenel, and Wilson to compute the E2-term of the Adams-Novikov spectral sequence for computing the stable homotopy groups of spheres. The E1-term 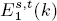of the spectral sequence is an Ext group of BP*BP-comodules. There is a sequence of Ext groups 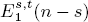for nonnegative integers n with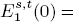 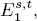and there are Bockstein spectral sequences computing a module 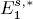(n – s) from 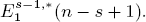So far, a small number of the E1-terms are determined. Here, we determine the 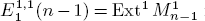for p > 2 and n > 3 by computing the Bockstein spectral sequence with E1-term 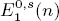for s = 1, 2. As an application, we study the nontriviality of the action of α1 and β1 in the homotopy groups of the second Smith-Toda spectrum V(2).

Keywords

55Q9955T9955Q45
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 207 , September 2012 , pp. 139 - 157
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2012

References

[1] Arita, Y. and Shimomura, K., The chromatic E1-term H1 M1 1 at the prime 3, Hiroshima Math. J. 26 (1996), 415–431.Google Scholar
[2] Henn, H.-W., Centralizers of elementary abelian p-subgroups and mod-p cohomology of profinite groups, Duke Math. J. 91 (1998), 561–585.Google Scholar
[3] Hirata, H. and Shimomura, K., The chromatic E1-term H1M2 1 for an odd prime, in preparation.Google Scholar
[4] Kraines, D., Massey higher products, Trans. Amer. Math. Soc. 124 (1966), 431–449.CrossRefGoogle Scholar
[5] May, J. P., “A general algebraic approach to Steenrod operations” in The Steenrod Algebra and its Applications (Columbus, Ohio, 1970), Lecture Notes in Math. 168, Springer, Berlin, 1970, 153–231.Google Scholar
[6] Miller, H. R. and Ravenel, D. C., Morava stabilizer algebras and the localization of Novikov’s E2-term, Duke Math. J. 44 (1977), 433–447.Google Scholar
[7] Miller, H. R., Ravenel, D. C., and Wilson, W. S., Periodic phenomena in AdamsNovikov spectral sequence, Ann. of Math. (2) 106 (1977), 469–516.Google Scholar
[8] Nakai, H., The chromatic E1-term H0M1 2 for p> 3, New York J. Math. 6 (2000), 21–54.Google Scholar
[9] Nakai, H., The structure of Mem. Fac. Sci. Kochi Univ. Ser. A Math. 23 (2002), 27–44.Google Scholar
[10] Ravenel, D. C., The cohomology of the Morava stabilizer algebras, Math. Z. 152 (1977), 287–297.CrossRefGoogle Scholar
[11] Ravenel, D. C., Localization with respect to certain periodic homology theories, Amer. J. Math. 106 (1984), 351–414.Google Scholar
[12] Ravenel, D. C., Nilpotence and Periodicity in Stable Homotopy Theory, Ann. of Math. Stud. 128, Princeton University Press, Princeton, 1992.Google Scholar
[13] Ravenel, D. C., Complex Cobordism and Stable Homotopy Groups of Spheres, AMS Chelsea Publishing, Providence, 2004.Google Scholar
[14] Shimomura, K., On the Adams-Novikov spectral sequence and products of β-elements, Hiroshima Math. J. 16 (1986), 209–224.CrossRefGoogle Scholar
[15] Shimomura, K., The chromatic E1-term H1M2 1 and its application to the homology of the Toda-Smith spectrum V(1), J. Fac. Educ. Tottori Univ. (Nat. Sci.) 39 (1990), 63–83; Correction, J. Fac. Educ. Tottori Univ. (Nat. Sci.) 41 (1992), 7–11.Google Scholar
[16] Shimomura, K., The chromatic E1-term , J. Fac. Educ. Tottori Univ. (Nat. Sci.) 39 (1990), 103–121.Google Scholar
[17] Shimomura, K., The homotopy groups of the L2-localized Toda-Smith spectrum V(1) at the prime 3, Trans. Amer. Math. Soc. 349 (1997), 1821-1850.Google Scholar
[18] Shimomura, K., The homotopy groups of the L2-localized mod 3 Moore spectrum, J. Math. Soc. Japan 52 (2000), 65–90.CrossRefGoogle Scholar
[19] Shimomura, K. and H. Tamura, Nontriviality of some compositions of β-elements in the stable homotopy of the Moore spaces, Hiroshima Math. J. 16 (1986), 121–133.Google Scholar
[20] Shimomura, K. and Wang, X., The homotopy groups π*(L2S0) at the prime 3, Topology 41 (2002), 1183–1198.CrossRefGoogle Scholar
[21] Shimomura, K. and Yabe, A., The homotopy groups π*(L2S0), Topology 34 (1995), 261–289.Google Scholar
[22] Toda, H., On spectra realizing exterior parts of the Steenrod algebra, Topology 10 (1971), 53–65.Google Scholar