Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T20:45:53.914Z Has data issue: false hasContentIssue false
  • English
  • Français

The Centralizer of a Nilpotent Section

Published online by Cambridge University Press:  11 January 2016

George J. McNinch
George J. McNinch*
Affiliation:
Department of Mathematics, Tufts University, 503 Boston Avenue, Medford, MA 02155, USA, [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be an algebraically closed field and let G be a semisimple F-algebraic group for which the characteristic of F is very good. If X ∈ Lie(G) = Lie(G)(F) is a nilpotent element in the Lie algebra of G, and if C is the centralizer in G of X, we show that (i) the root datum of a Levi factor of C, and (ii) the component group C/C° both depend only on the Bala-Carter label of X; i.e. both are independent of very good characteristic. The result in case (ii) depends on the known case when G is (simple and) of adjoint type.

The proofs are achieved by studying the centralizer 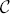of a nilpotent section X in the Lie algebra of a suitable semisimple group scheme over a Noetherian, normal, local ring 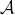. When the centralizer of X is equidimensional on Spec(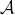), a crucial result is that locally in the étale topology there is a smooth 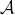-subgroup scheme L of 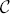such that Lt is a Levi factor of 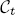for each t ∈ Spec ().

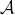Keywords

20G15
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 190 , 2008 , pp. 129 - 181
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2008

References

[Al 79] Alekseevskiĭ, A. V., Component groups of centralizes of unipotent elements in semisimple algebraic groups, Akad. Nauk Gruzin. SSR Trudy Tbiliss. Mat. Inst. Razmadze, 62 (1979). Collection of articles on algebra, 2.Google Scholar
[Bor 91] Borel, Armand, Linear Algebraic Groups, 2nd ed., Grad. Texts in Math., vol. 126, Springer Verlag, 1991.Google Scholar
[Ca 93] Carter, Roger W., Finite groups of Lie type: conjugacy classes and complex characters, John Wiley & Sons Ltd., Chichester, 1993. Reprint of the 1985 original.Google Scholar
[EGA IV] Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Inst. Hautes Études Sci. Publ. Math., 28 (1966), 255.Google Scholar
[SGA 1] Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Documents Mathématiques 3, Société Mathématique de France, Paris, 2003. Séminaire de Géometrie Algébrique du Bois Marie. [Updated and annotated reprint of the 1971 original publication in Lecture Notes in Math., 224, Springer, Berlin.]Google Scholar
[SGA 3] Grothendieck, A. and Demazure, M., Schémas en Groupes (SGA 3). I, II, III, Lectures Notes in Math., vol. 151, 152, 153, Springer Verlag, Heidelberg, 1965. Séminaire de Géometrie Algébrique du Bois Marie.Google Scholar
[Hu 95] Humphreys, James E., Conjugacy classes in semisimple algebraic groups, Math. Surveys and Monographs, vol. 43, Amer. Math. Soc., 1995.Google Scholar
[Ja 04] Jantzen, Jens Carsten, Nilpotent orbits in representation theory, Lie Theory: Lie Algebras and Representations (J.-P. Anker and B. Orsted, eds.), Progress in Mathematics, vol. 228, Birkhäuser, Boston, 2004, pp. 1–211.Google Scholar
[Ja 03] Jantzen, Jens Carsten, Representations of algebraic groups, 2nd ed., Mathematical Surveys and Monographs, vol. 107, American Mathematical Society, Providence, RI, 2003.Google Scholar
[Ke78] Kempf, George R., Instability in invariant theory, Ann. of Math. (2), 108 (1978), no. 2, 299–316.CrossRefGoogle Scholar
[KMRT] Knus, Max-Albert, Alexander Merkurjev, Markus Rost and Jean-Pierre Tignol, The book of involutions, Amer. Math. Soc., Colloq. Publ., vol. 44, Amer. Math. Soc., 1998.Google Scholar
[Li 02] Liu, Qing, Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, vol. 6, Oxford University Press, 2002. Translated from the French by Reinie Erné.Google Scholar
[MS 03] McNinch, George J. and Sommers, Eric, Component groups of unipotent centralizes in good characteristic, J. Algebra, 260 (2003), no. 1, 323–337. Special issue celebrating the 80th birthday of Robert Steinberg. math.RT/0204275.CrossRefGoogle Scholar
[MT 07] McNinch, George J. and Testerman, Donna M., Completely reducible SL(2)-homomorphisms, Trans. Amer. Math. Soc., 359 (2007), no. 9, 4489–4510.CrossRefGoogle Scholar
[Mc 04] McNinch, George J., Nilpotent orbits over ground fields of good characteristic, Math. Annalen, 329 (2004), 49–85. arXiv:math.RT/0209151.CrossRefGoogle Scholar
[Mc 05] McNinch, George J., Optimal SL(2)-homomorphisms, Comment. Math. Helv., 80 (2005), 391–426. arXiv:math.RT/0309385.CrossRefGoogle Scholar
[Mc 06] McNinch, George J., On the centralizer of the sum of commuting nilpotent elements, J. Pure and Applied Algebra, 206 (2006), 123–140. arXiv:math.RT/0412283.CrossRefGoogle Scholar
[Mil 80] Milne, James, Etale Cohomology, Princeton University Press, 1980.CrossRefGoogle Scholar
[Miz 80] Mizuno, Kenzo, The conjugate classes of unipotent elements of the Chevalley groups E7 and E8 , Tokyo J. Math., 3 (1980), no. 2, 391–461.CrossRefGoogle Scholar
[Pr 03] Premet, Alexander, Nilpotent orbits in good characteristic and the Kempf-Rousseau theory, J. Algebra, 260 (2003), no. 1, 338–366. Special issue celebrating the 80th birthday of Robert Steinberg.CrossRefGoogle Scholar
[Ri 82] Richardson, R. W., On orbits of algebraic groups and Lie groups, Bull. Austral. Math. Soc., 25 (1982), no. 1, 1–28.CrossRefGoogle Scholar
[Se 79] Serre, Jean-Pierre, Local Fields, Springer Verlag, 1979.CrossRefGoogle Scholar
[Ser 05] Serre, Jean-Pierre, Complète Réductibilité, Astérisque, 299 (2005), Exposés 924-937, pp. 195–217. Séminaire Bourbaki 2003/2004.Google Scholar
[So 98] Sommers, Eric, A generalization of the Bala-Carter theorem for nilpotent orbits, Internat. Math. Res. Notices (1998), no. 11, 539–562.CrossRefGoogle Scholar
[Sp 98] Springer, Tonny A., Linear algebraic groups, 2nd ed., Progr. in Math., vol. 9, Birkhäuser, Boston, 1998.Google Scholar
[St 68] Steinberg, Robert, Endomorphisms of linear algebraic groups, Memoirs of the American Mathematical Society, No. 80, American Mathematical Society, Providence, R.I., 1968.Google Scholar