Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T17:09:53.157Z Has data issue: false hasContentIssue false
  • English
  • Français

C∞-Convergence of Circle Patterns to Minimal Surfaces

Published online by Cambridge University Press:  11 January 2016

Shi-Yi Lan  and
Dao-Qing Dai
Shi-Yi Lan
Affiliation:
Department of Mathematics, Guangxi University for Nationalities, Nanning 530006, P. R. China
Dao-Qing Dai
Affiliation:
Department of Mathematics, Sun Yat-Sen (Zhongshan) University, Guangzhou 510275, P. R. China, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a smooth minimal surface F: Ω → ℝ3 defined on a simply connected region Ω in the complex plane ℂ, there is a regular SG circle pattern 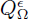. By the Weierstrass representation of F and the existence theorem of SG circle patterns, there exists an associated SG circle pattern 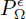in ℂ with the combinatoric of 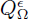. Based on the relationship between the circle pattern 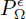and the corresponding discrete minimal surface F∊: 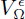→ ℝ3 defined on the vertex set 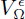of the graph of 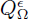, we show that there exists a family of discrete minimal surface Γ∊: 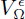→ ℝ3, which converges in C∞(Ω) to the minimal surface F: Ω → ℝ3 as ∊ → 0.

Keywords

52C2653A1053C42
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 194 , 2009 , pp. 149 - 167
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2009

References

[1] Agafonov, S. I., Imbedded circle patterns with the combinatorics of the square grid and discrete Painlevé equations, Discrete Comput. Geom., 29 (2003), no. 2, 305–319.Google Scholar
[2] Bobenko, A. I., Hoffmann, T., and Springborn, B. A., Minimal surfaces from circle patterns: Geometry from combinatorics, Ann. of Math., 164 (2006), 231–264.Google Scholar
[3] Bobenko, A. I. and Pinkall, U., Disrete isothermic surfaces, J. Reine Angew. Math., 475 (1996), 187–208.Google Scholar
[4] Bokenko, A. I. and Suris, Y. B., Discrete Differnetial Geometry. Consistency as Intergrabilty, arXiv:math.DG/0504358 v1, 18 Apr. 2005.Google Scholar
[5] Doyle, P. G., He, Z.-X. and Rodin, B., Second derivatives of circle packings and conformal mappings, Disrete Comput. Geom., 11 (1994), 35–49.Google Scholar
[6] Dierkes, U., Hildebrandt, S., Küster, A. and Wohlrab, O., Minimal Surfaces I, Springer-Verlag, Berlin, 1992.Google Scholar
[7] He, Z.-X. and Schramm, O., On the convergence of circle packings to the Riemann map, Invent. Math., 125 (1996), 285–305.Google Scholar
[8] He, Z.-X. and Schramm, O., The C∞-convergence of hexagonal disk packings to the Riemann map, Acta Math., 180 (1998), 219–245.Google Scholar
[9] Kapouleas, N., Complete embedded minimal surfaces of finite total curvature, J. Differential Geom., 47 (1997), 95–169.Google Scholar
[10] Nitsche, J. C., Lectures on Minimal Surfaces, Vol. 1, Cambridge Univ. Press, 1989.Google Scholar
[11] Rodin, B. and Sullivan, D., The convergence of circle packings to the Riemann mapping, J. Differential Geom., 26 (1987), 349–360.Google Scholar
[12] Schramm, O., Circle patterns with the combinatorics of the square grid, Duke Math. J., 86 (1997), no. 2, 347–389.Google Scholar
[13] Thurston, W., The geometry and topology of 3-manifolds, Chapter 13, Princeton University Notes, Princeton, N.J., 1980.Google Scholar