Published online by Cambridge University Press: 27 February 2018
Ringel’s right-strongly quasi-hereditary algebras are a distinguished class of quasi-hereditary algebras of Cline–Parshall–Scott. We give characterizations of these algebras in terms of heredity chains and right rejective subcategories. We prove that any artin algebra of global dimension at most two is right-strongly quasi-hereditary. Moreover we show that the Auslander algebra of a representation-finite algebra 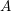 $A$ is strongly quasi-hereditary if and only if
$A$ is strongly quasi-hereditary if and only if 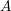 $A$ is a Nakayama algebra.
$A$ is a Nakayama algebra.
This work is supported by Grant-in-Aid for JSPS Fellowships No. H15J09492.