No CrossRef data available.
Article contents
SELMER GROUPS OF ELLIPTIC CURVES OVER THE 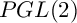 $PGL(2)$ EXTENSION
$PGL(2)$ EXTENSION
Published online by Cambridge University Press: 30 May 2022
Abstract
Iwasawa theory of elliptic curves over noncommutative
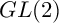 $GL(2)$
extension has been a fruitful area of research. Over such a noncommutative p-adic Lie extension, there exists a structure theorem providing the structure of the dual Selmer groups for elliptic curves in terms of reflexive ideals in the Iwasawa algebra. The central object of this article is to study Iwasawa theory over the
$GL(2)$
extension has been a fruitful area of research. Over such a noncommutative p-adic Lie extension, there exists a structure theorem providing the structure of the dual Selmer groups for elliptic curves in terms of reflexive ideals in the Iwasawa algebra. The central object of this article is to study Iwasawa theory over the
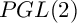 $PGL(2)$
extension and connect it with Iwasawa theory over the
$PGL(2)$
extension and connect it with Iwasawa theory over the
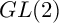 $GL(2)$
extension, deriving consequences to the structure theorem when the reflexive ideal is the augmentation ideal of the center. We also show how the dual Selmer group over the
$GL(2)$
extension, deriving consequences to the structure theorem when the reflexive ideal is the augmentation ideal of the center. We also show how the dual Selmer group over the
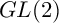 $GL(2)$
extension being torsion is related with that of the
$GL(2)$
extension being torsion is related with that of the
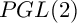 $PGL(2)$
extension.
$PGL(2)$
extension.
MSC classification
- Type
- Article
- Information
- Copyright
- © (2022) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
This work started with the Pacific Institute for the Mathematical Sciences and the Centre National de la Recherche Scientifique research funding received by Jishnu Ray. Later on, he also received funding from the Tata Institute of Fundamental Research and the Institute for Advancing Intelligence, The Chatterjee Group—Centres for Research and Education in Science and Technology in writing the revised versions. R. Sujatha gratefully acknowledges support from the Natural Sciences and Engineering Research Council of Canada Discovery grant 2019-03987.



