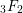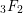1 Introduction
For
![]() $\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{j}\in \mathbb{C}$
with
$\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{j}\in \mathbb{C}$
with
![]() $\unicode[STIX]{x1D6FD}_{j}\not \in \mathbb{Z}_{{\leqslant}0}$
, the generalized hypergeometric function is defined by a power series expansion
$\unicode[STIX]{x1D6FD}_{j}\not \in \mathbb{Z}_{{\leqslant}0}$
, the generalized hypergeometric function is defined by a power series expansion
where
denotes the Pochhammer symbol. When
![]() $p=2$
, this is called the Gauss hypergeometric function. This has an analytic continuation to
$p=2$
, this is called the Gauss hypergeometric function. This has an analytic continuation to
![]() $\mathbb{C}$
, and then becomes a multivalued function which is holomorphic on
$\mathbb{C}$
, and then becomes a multivalued function which is holomorphic on
![]() $\mathbb{C}\setminus \{0,1\}$
. A number of formulas have been discovered since 19th century (e.g., [Reference Olver, Lozier, Boisvert and Clark10, Chapters 15, 16]), and they have been applied in various areas in mathematics. At present, the theory of hypergeometric function is one of the most important tools in mathematics.
$\mathbb{C}\setminus \{0,1\}$
. A number of formulas have been discovered since 19th century (e.g., [Reference Olver, Lozier, Boisvert and Clark10, Chapters 15, 16]), and they have been applied in various areas in mathematics. At present, the theory of hypergeometric function is one of the most important tools in mathematics.
In [Reference Asakura, Otsubo and Terasoma5], we discussed the special values of
![]() $_{3}F_{2}({1,1,q\atop a,b};x)$
at
$_{3}F_{2}({1,1,q\atop a,b};x)$
at
![]() $x=1$
, and gave a sufficient condition for it to be a
$x=1$
, and gave a sufficient condition for it to be a
![]() $\overline{\mathbb{Q}}$
-linear combination of logarithms of algebraic numbers, namely
$\overline{\mathbb{Q}}$
-linear combination of logarithms of algebraic numbers, namely
 $$\begin{eqnarray}\displaystyle & & \displaystyle \,_{3}F_{2}{1,1,q\atop a,b};1\in \overline{\mathbb{Q}}+\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }\nonumber\\ \displaystyle & & \displaystyle \quad :=\left\{\left.a+\mathop{\sum }_{i=1}^{n}b_{i}\log c_{i}\,\right|a,b_{i},c_{i}\in \overline{\mathbb{Q}},\,c_{i}\neq 0,\,n\in \mathbb{Z}_{{\geqslant}0}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \,_{3}F_{2}{1,1,q\atop a,b};1\in \overline{\mathbb{Q}}+\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }\nonumber\\ \displaystyle & & \displaystyle \quad :=\left\{\left.a+\mathop{\sum }_{i=1}^{n}b_{i}\log c_{i}\,\right|a,b_{i},c_{i}\in \overline{\mathbb{Q}},\,c_{i}\neq 0,\,n\in \mathbb{Z}_{{\geqslant}0}\right\}.\nonumber\end{eqnarray}$$
The goal of this paper is to give its functional version. To be precise, set
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\mathbb{Q}(x)}+\overline{\mathbb{Q}(x)}\log \overline{\mathbb{Q}(x)}^{\times }\nonumber\\ \displaystyle & & \displaystyle \quad :=\left\{\left.f+\mathop{\sum }_{i=1}^{n}g_{i}\log h_{i}\,\right|f,g_{i},h_{i}\in \overline{\mathbb{Q}(x)},\,h_{i}\neq 0,\,n\in \mathbb{Z}_{{\geqslant}0}\right\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\mathbb{Q}(x)}+\overline{\mathbb{Q}(x)}\log \overline{\mathbb{Q}(x)}^{\times }\nonumber\\ \displaystyle & & \displaystyle \quad :=\left\{\left.f+\mathop{\sum }_{i=1}^{n}g_{i}\log h_{i}\,\right|f,g_{i},h_{i}\in \overline{\mathbb{Q}(x)},\,h_{i}\neq 0,\,n\in \mathbb{Z}_{{\geqslant}0}\right\}\nonumber\end{eqnarray}$$
where
![]() $\overline{\mathbb{Q}(x)}$
denotes the algebraic closure of the field of rational functions
$\overline{\mathbb{Q}(x)}$
denotes the algebraic closure of the field of rational functions
![]() $\mathbb{Q}(x)$
. We say that the logarithmic formula holds for a function
$\mathbb{Q}(x)$
. We say that the logarithmic formula holds for a function
![]() $F(x)$
if it belongs to the above set. The main theorem gives a sufficient condition on
$F(x)$
if it belongs to the above set. The main theorem gives a sufficient condition on
![]() $(a,b,q)$
for
$(a,b,q)$
for
![]() $_{3}F_{2}({1,1,q\atop a,b};x)$
to satisfy a logarithmic formula. Recall that two proofs are presented in [Reference Asakura, Otsubo and Terasoma5]. One of the proofs uses hypergeometric fibrations and the other uses Fermat surfaces. In this paper we follow the method of hypergeometric fibrations, while employing a new ingredient from [Reference Asakura and Otsubo3]. It seems impossible to prove the functional log formula using the method of Fermat surfaces.
$_{3}F_{2}({1,1,q\atop a,b};x)$
to satisfy a logarithmic formula. Recall that two proofs are presented in [Reference Asakura, Otsubo and Terasoma5]. One of the proofs uses hypergeometric fibrations and the other uses Fermat surfaces. In this paper we follow the method of hypergeometric fibrations, while employing a new ingredient from [Reference Asakura and Otsubo3]. It seems impossible to prove the functional log formula using the method of Fermat surfaces.
By developing the technique here, we can get explicit log formulas in some cases. For example, let
 $$\begin{eqnarray}\displaystyle e_{1}(x) & := & \displaystyle \frac{1}{2}+x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle e_{2}(x) & := & \displaystyle \frac{1}{2}+e^{-2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,e^{2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle e_{3}(x) & := & \displaystyle \frac{1}{2}+e^{2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,e^{-2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{1}(x) & := & \displaystyle \frac{1}{2}+x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle e_{2}(x) & := & \displaystyle \frac{1}{2}+e^{-2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,e^{2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle e_{3}(x) & := & \displaystyle \frac{1}{2}+e^{2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}+\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\\ \displaystyle & & \displaystyle +\,e^{-2\unicode[STIX]{x1D70B}i/3}x^{-1/3}\left(-\frac{1}{4}+\frac{x}{8}-\frac{1}{4}\sqrt{1-x}\right)^{1/3}\nonumber\end{eqnarray}$$
Then

However, there remain technical difficulties arising from algebraic cycles to obtain explicit log formulas in more general cases.
2 Main theorem
Let
![]() $\hat{\mathbb{Z}}=\mathop{\varprojlim }\nolimits_{n}\mathbb{Z}/n\mathbb{Z}$
be the completion, and
$\hat{\mathbb{Z}}=\mathop{\varprojlim }\nolimits_{n}\mathbb{Z}/n\mathbb{Z}$
be the completion, and
![]() $\hat{\mathbb{Z}}^{\times }=\mathop{\varprojlim }\nolimits_{n}(\mathbb{Z}/n\mathbb{Z})^{\times }$
the group of units. The ring
$\hat{\mathbb{Z}}^{\times }=\mathop{\varprojlim }\nolimits_{n}(\mathbb{Z}/n\mathbb{Z})^{\times }$
the group of units. The ring
![]() $\hat{\mathbb{Z}}$
acts on the additive group
$\hat{\mathbb{Z}}$
acts on the additive group
![]() $\mathbb{Q}/\mathbb{Z}$
in a natural way, and then it induces
$\mathbb{Q}/\mathbb{Z}$
in a natural way, and then it induces
![]() $\hat{\mathbb{Z}}^{\times }\cong \text{Aut}(\mathbb{Q}/\mathbb{Z})$
. We denote by
$\hat{\mathbb{Z}}^{\times }\cong \text{Aut}(\mathbb{Q}/\mathbb{Z})$
. We denote by
![]() $\{x\}:=x-\lfloor x\rfloor$
the fractional part of
$\{x\}:=x-\lfloor x\rfloor$
the fractional part of
![]() $x\in \mathbb{Q}$
. The map
$x\in \mathbb{Q}$
. The map
![]() $\{-\}:\mathbb{Q}\rightarrow [0,1)$
factors through
$\{-\}:\mathbb{Q}\rightarrow [0,1)$
factors through
![]() $\mathbb{Q}/\mathbb{Z}$
, which we denote by the same notation.
$\mathbb{Q}/\mathbb{Z}$
, which we denote by the same notation.
Theorem 2.1. (Logarithmic formula)
Let
![]() $q,a,b\in \mathbb{Q}$
satisfy the property that none of
$q,a,b\in \mathbb{Q}$
satisfy the property that none of
![]() $q,a,b,q-a,q-b,q-a-b$
is an integer. Suppose
$q,a,b,q-a,q-b,q-a-b$
is an integer. Suppose
for
![]() $\forall s\in \hat{\mathbb{Z}}^{\times }$
. Then
$\forall s\in \hat{\mathbb{Z}}^{\times }$
. Then
for any integers
![]() $n_{i}>0$
.
$n_{i}>0$
.
As we shall see in Section 4, one can shift the indices
![]() $n_{i}$
,
$n_{i}$
,
![]() $q,a,b$
by arbitrary integers by applying differential operators. Thus it is enough to prove the log formula for
$q,a,b$
by arbitrary integers by applying differential operators. Thus it is enough to prove the log formula for
![]() $_{3}F_{2}({1,1,q\atop a,~b};x)$
.
$_{3}F_{2}({1,1,q\atop a,~b};x)$
.
Recall the main theorem of [Reference Asakura, Otsubo and Terasoma5] which asserts that if
for
![]() $\forall s\in \hat{\mathbb{Z}}^{\times }$
, then
$\forall s\in \hat{\mathbb{Z}}^{\times }$
, then
as long as it converges (
![]() $\Leftrightarrow$
$\Leftrightarrow$
![]() $a+b>q+2$
). It is easy to see (2.1)
$a+b>q+2$
). It is easy to see (2.1)
![]() $\Rightarrow$
(2.2) while the converse is no longer true (e.g.,
$\Rightarrow$
(2.2) while the converse is no longer true (e.g.,
![]() $(a,b,q)=(1/6,1/4,1/2)$
). Therefore Theorem 2.1 does not imply all of the main theorem of [Reference Asakura, Otsubo and Terasoma5].
$(a,b,q)=(1/6,1/4,1/2)$
). Therefore Theorem 2.1 does not imply all of the main theorem of [Reference Asakura, Otsubo and Terasoma5].
Conjecture 2.2. (Cf. [Reference Asakura, Otsubo and Terasoma5, Conjecture 5.2])
The converse of Theorem 2.1 is true.
In the seminal paper [Reference Beukers and Heckman7], Beukers and Heckman gave a necessary and sufficient condition for
![]() $_{p}F_{p-1}$
to be an algebraic function, or equivalently for its monodromy group to be finite. Let
$_{p}F_{p-1}$
to be an algebraic function, or equivalently for its monodromy group to be finite. Let
![]() $a_{i},b_{j}\in \mathbb{Q}$
. Then their theorem states that, under the condition that
$a_{i},b_{j}\in \mathbb{Q}$
. Then their theorem states that, under the condition that
![]() $\{a_{i}\}\neq \{b_{j}\}$
and
$\{a_{i}\}\neq \{b_{j}\}$
and
![]() $\{a_{i}\}\neq 0$
,
$\{a_{i}\}\neq 0$
,
if and only if
![]() $(\{sa_{1}\},\ldots ,\{sa_{p}\})$
and
$(\{sa_{1}\},\ldots ,\{sa_{p}\})$
and
![]() $(0,\{sb_{1}\},\ldots ,\{sb_{p-1}\})$
interlace for all
$(0,\{sb_{1}\},\ldots ,\{sb_{p-1}\})$
interlace for all
![]() $s\in \hat{\mathbb{Z}}^{\times }$
[Reference Beukers and Heckman7, Theorem 4.8]. Here we say that two sets
$s\in \hat{\mathbb{Z}}^{\times }$
[Reference Beukers and Heckman7, Theorem 4.8]. Here we say that two sets
![]() $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{p})$
and
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{p})$
and
![]() $(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{p})$
interlace if and only if
$(\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{p})$
interlace if and only if
when ordering
![]() $\unicode[STIX]{x1D6FC}_{1}<\cdots <\unicode[STIX]{x1D6FC}_{p}$
and
$\unicode[STIX]{x1D6FC}_{1}<\cdots <\unicode[STIX]{x1D6FC}_{p}$
and
![]() $\unicode[STIX]{x1D6FD}_{1}<\cdots <\unicode[STIX]{x1D6FD}_{p}$
. In this terminology, (2.1) is translated into that
$\unicode[STIX]{x1D6FD}_{1}<\cdots <\unicode[STIX]{x1D6FD}_{p}$
. In this terminology, (2.1) is translated into that
![]() $(0,\{sq\})$
and
$(0,\{sq\})$
and
![]() $(\{sa\},\{sb\})$
interlace. Our main Theorem 2.1 is not directly related to their theorem, while they are obviously comparable.
$(\{sa\},\{sb\})$
interlace. Our main Theorem 2.1 is not directly related to their theorem, while they are obviously comparable.
3 Hypergeometric fibrations
We mean by a fibration over a ring
![]() $k$
a projective flat morphism of quasiprojective smooth
$k$
a projective flat morphism of quasiprojective smooth
![]() $k$
-schemes.
$k$
-schemes.
3.1 Definition
Let
![]() $f:X\rightarrow \mathbb{P}^{1}$
be a fibration over a field
$f:X\rightarrow \mathbb{P}^{1}$
be a fibration over a field
![]() $k$
. For simplicity we assume
$k$
. For simplicity we assume
![]() $k=\overline{k}$
and fix an embedding
$k=\overline{k}$
and fix an embedding
![]() $k\subset \mathbb{C}$
. Let
$k\subset \mathbb{C}$
. Let
![]() $R$
be a finite-dimensional semisimple commutative
$R$
be a finite-dimensional semisimple commutative
![]() $\mathbb{Q}$
-algebra. We mean by a multiplication on
$\mathbb{Q}$
-algebra. We mean by a multiplication on
![]() $R^{1}f_{\ast }\mathbb{Q}$
by
$R^{1}f_{\ast }\mathbb{Q}$
by
![]() $R$
a homomorphism
$R$
a homomorphism
![]() $\unicode[STIX]{x1D70C}:R\rightarrow \text{End}_{\text{VHS}}(R^{1}f_{\ast }\mathbb{Q}|_{U})$
of rings where
$\unicode[STIX]{x1D70C}:R\rightarrow \text{End}_{\text{VHS}}(R^{1}f_{\ast }\mathbb{Q}|_{U})$
of rings where
![]() $U\subset \mathbb{P}^{1}$
is the maximal Zariski open set such that
$U\subset \mathbb{P}^{1}$
is the maximal Zariski open set such that
![]() $f$
is smooth over
$f$
is smooth over
![]() $U$
. Let
$U$
. Let
![]() $e:R\rightarrow E$
be a projection onto a number field
$e:R\rightarrow E$
be a projection onto a number field
![]() $E$
. We say
$E$
. We say
![]() $f$
is a hypergeometric fibration with multiplication by
$f$
is a hypergeometric fibration with multiplication by
![]() $(R,e)$
(HG fibration) if the following conditions hold. We fix an inhomogeneous coordinate
$(R,e)$
(HG fibration) if the following conditions hold. We fix an inhomogeneous coordinate
![]() $t\in \mathbb{P}^{1}$
.
$t\in \mathbb{P}^{1}$
.
(a)
 $f$
is smooth over
$f$
is smooth over
 $\mathbb{P}^{1}\setminus \{0,1,\infty \}$
,
$\mathbb{P}^{1}\setminus \{0,1,\infty \}$
,(b)
 $\dim _{E}H^{1}(X_{t},\mathbb{Q})(e)=2$
where
$\dim _{E}H^{1}(X_{t},\mathbb{Q})(e)=2$
where
 $X_{t}=f^{-1}(t)$
is a general fiber and we write
$X_{t}=f^{-1}(t)$
is a general fiber and we write
 $V(e):=E\otimes _{e,R}V$
the
$V(e):=E\otimes _{e,R}V$
the
 $e$
-part,
$e$
-part,(c) Let
 $\text{Pic}_{f}^{0}\rightarrow \mathbb{P}^{1}\setminus \{0,1,\infty \}$
be the Picard fibration whose general fiber is the Picard variety
$\text{Pic}_{f}^{0}\rightarrow \mathbb{P}^{1}\setminus \{0,1,\infty \}$
be the Picard fibration whose general fiber is the Picard variety
 $\text{Pic}^{0}(f^{-1}(t))$
, and let
$\text{Pic}^{0}(f^{-1}(t))$
, and let
 $\text{Pic}_{f}^{0}(e)$
be the component associated to the
$\text{Pic}_{f}^{0}(e)$
be the component associated to the
 $e$
-part
$e$
-part
 $R^{1}f_{\ast }\mathbb{Q}(e)$
(this is well defined up to isogeny). Then
$R^{1}f_{\ast }\mathbb{Q}(e)$
(this is well defined up to isogeny). Then
 $\text{Pic}_{f}^{0}(e)\rightarrow \mathbb{P}^{1}\setminus \{0,1,\infty \}$
has totally degenerate semistable reduction at
$\text{Pic}_{f}^{0}(e)\rightarrow \mathbb{P}^{1}\setminus \{0,1,\infty \}$
has totally degenerate semistable reduction at
 $t=1$
.
$t=1$
.
The last condition (c) is equivalent to saying that the local monodromy
![]() $T$
on
$T$
on
![]() $H^{1}(X_{t},\mathbb{Q})(e)$
at
$H^{1}(X_{t},\mathbb{Q})(e)$
at
![]() $t=1$
is unipotent and the rank of log monodromy
$t=1$
is unipotent and the rank of log monodromy
![]() $N:=\log (T)$
is maximal, namely
$N:=\log (T)$
is maximal, namely
![]() $\text{rank}(N)={\textstyle \frac{1}{2}}\dim _{\mathbb{Q}}H^{1}(X_{t},\mathbb{Q})(e)$
(
$\text{rank}(N)={\textstyle \frac{1}{2}}\dim _{\mathbb{Q}}H^{1}(X_{t},\mathbb{Q})(e)$
(
![]() $=[E:\mathbb{Q}]$
by condition (b)).
$=[E:\mathbb{Q}]$
by condition (b)).
3.2 HG fibration of Gauss type
Let
![]() $f:X\rightarrow \mathbb{P}^{1}$
be a fibration over
$f:X\rightarrow \mathbb{P}^{1}$
be a fibration over
![]() $\overline{\mathbb{Q}}$
whose general fiber
$\overline{\mathbb{Q}}$
whose general fiber
![]() $X_{t}=f^{-1}(t)$
is the nonsingular projective model of the affine curve
$X_{t}=f^{-1}(t)$
is the nonsingular projective model of the affine curve
![]() $f$
is smooth outside
$f$
is smooth outside
![]() $\{0,1,\infty \}$
so that the condition (a) is satisfied. The group
$\{0,1,\infty \}$
so that the condition (a) is satisfied. The group
![]() $\unicode[STIX]{x1D707}_{N}$
of
$\unicode[STIX]{x1D707}_{N}$
of
![]() $N$
th roots of unity acts on
$N$
th roots of unity acts on
![]() $f^{-1}(t)$
by
$f^{-1}(t)$
by
![]() $(x,y,t)\mapsto (x,\unicode[STIX]{x1D701}y,t)$
for
$(x,y,t)\mapsto (x,\unicode[STIX]{x1D701}y,t)$
for
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
, which gives rise to a multiplication on
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
, which gives rise to a multiplication on
![]() $R^{1}f_{\ast }\mathbb{Q}$
by the group ring
$R^{1}f_{\ast }\mathbb{Q}$
by the group ring
![]() $R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}]$
.
$R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}]$
.
Lemma 3.1. [Reference Asakura and Otsubo4, Proposition 3.1] Let
![]() $e_{0}:R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}]\rightarrow E_{0}$
be a projection onto a number field
$e_{0}:R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}]\rightarrow E_{0}$
be a projection onto a number field
![]() $E_{0}$
. Then
$E_{0}$
. Then
![]() $(R_{0},e_{0})$
satisfies the conditions (b) and (c) if and only if
$(R_{0},e_{0})$
satisfies the conditions (b) and (c) if and only if
![]() $ad\not \equiv 0$
and
$ad\not \equiv 0$
and
![]() $bd\not \equiv 0$
modulo
$bd\not \equiv 0$
modulo
![]() $N$
where
$N$
where
![]() $d:=\sharp \text{Ker}[\unicode[STIX]{x1D707}_{N}\rightarrow R_{0}^{\times }\overset{e_{0}}{\rightarrow }E_{0}^{\times }]$
.
$d:=\sharp \text{Ker}[\unicode[STIX]{x1D707}_{N}\rightarrow R_{0}^{\times }\overset{e_{0}}{\rightarrow }E_{0}^{\times }]$
.
Definition 3.2. We say that
![]() $f$
is a HG fibration of Gauss type with multiplication by
$f$
is a HG fibration of Gauss type with multiplication by
![]() $(\mathbb{Q}[\unicode[STIX]{x1D707}_{N}],e)$
if
$(\mathbb{Q}[\unicode[STIX]{x1D707}_{N}],e)$
if
![]() $ad\not \equiv 0$
and
$ad\not \equiv 0$
and
![]() $bd\not \equiv 0$
modulo
$bd\not \equiv 0$
modulo
![]() $N$
.
$N$
.
Let
![]() $\unicode[STIX]{x1D712}:R_{0}\rightarrow \overline{\mathbb{Q}}$
be a homomorphism of
$\unicode[STIX]{x1D712}:R_{0}\rightarrow \overline{\mathbb{Q}}$
be a homomorphism of
![]() $\mathbb{Q}$
-algebras factoring through
$\mathbb{Q}$
-algebras factoring through
![]() $e$
. Let
$e$
. Let
![]() $n$
be an integer such that
$n$
be an integer such that
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
for all
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
for all
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
. Note
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
. Note
![]() $\gcd (n,N)=1$
. By [Reference Archinard1, p. 917, (13)],
$\gcd (n,N)=1$
. By [Reference Archinard1, p. 917, (13)],
![]() $H_{\text{dR}}^{1}(X_{t})(\unicode[STIX]{x1D712})\cap H^{1,0}$
is spanned by the 1-form
$H_{\text{dR}}^{1}(X_{t})(\unicode[STIX]{x1D712})\cap H^{1,0}$
is spanned by the 1-form
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D714}_{n}:={\displaystyle \frac{x^{a_{n}}(1-x)^{b_{n}}(1-tx)^{c_{n}}}{y^{n}}}\,dx, & \displaystyle \nonumber\\ \displaystyle & a_{n}:=\left\lfloor {\displaystyle \frac{an}{N}}\right\rfloor ,\qquad b_{n}:=\left\lfloor {\displaystyle \frac{bn}{N}}\right\rfloor ,\qquad c_{n}:=\left\lfloor {\displaystyle \frac{Nn-bn}{N}}\right\rfloor =n-b_{n}-1. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D714}_{n}:={\displaystyle \frac{x^{a_{n}}(1-x)^{b_{n}}(1-tx)^{c_{n}}}{y^{n}}}\,dx, & \displaystyle \nonumber\\ \displaystyle & a_{n}:=\left\lfloor {\displaystyle \frac{an}{N}}\right\rfloor ,\qquad b_{n}:=\left\lfloor {\displaystyle \frac{bn}{N}}\right\rfloor ,\qquad c_{n}:=\left\lfloor {\displaystyle \frac{Nn-bn}{N}}\right\rfloor =n-b_{n}-1. & \displaystyle \nonumber\end{eqnarray}$$
Let
![]() $P_{1}$
(resp.
$P_{1}$
(resp.
![]() $P_{2}$
) be a point of
$P_{2}$
) be a point of
![]() $X_{t}$
above
$X_{t}$
above
![]() $x=0$
(resp.
$x=0$
(resp.
![]() $x=1$
). There are
$x=1$
). There are
![]() $\text{gcd}(N,a)$
-points above
$\text{gcd}(N,a)$
-points above
![]() $x=0$
(resp.
$x=0$
(resp.
![]() $\text{gcd}(N,b)$
-points above
$\text{gcd}(N,b)$
-points above
![]() $x=1$
). Let
$x=1$
). Let
![]() $u$
be a path from
$u$
be a path from
![]() $P_{1}$
to
$P_{1}$
to
![]() $P_{2}$
above the real interval
$P_{2}$
above the real interval
![]() $x\in [0,1]$
. It defines a homology cycle
$x\in [0,1]$
. It defines a homology cycle
![]() $u\in H_{1}(X_{t},\{P_{1},P_{2}\};\mathbb{Z})$
with boundary. Put
$u\in H_{1}(X_{t},\{P_{1},P_{2}\};\mathbb{Z})$
with boundary. Put
![]() $d_{1}:=\text{gcd}(N,a)$
,
$d_{1}:=\text{gcd}(N,a)$
,
![]() $d_{2}:=\text{gcd}(N,b)$
. Let
$d_{2}:=\text{gcd}(N,b)$
. Let
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D707}_{N}$
be an automorphism. Since
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D707}_{N}$
be an automorphism. Since
![]() $\unicode[STIX]{x1D70E}^{d_{1}}P_{1}=P_{1}$
and
$\unicode[STIX]{x1D70E}^{d_{1}}P_{1}=P_{1}$
and
![]() $\unicode[STIX]{x1D70E}^{d_{2}}P_{2}=P_{2}$
, one has a homology cycle
$\unicode[STIX]{x1D70E}^{d_{2}}P_{2}=P_{2}$
, one has a homology cycle
By an integral expression of Gauss hypergeometric functions (e.g., [Reference Bailey6, p. 4, 1.5] or [Reference Slater11, p. 20, (1.6.6)]), one has
where
![]() $B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}):=\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FD})/\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
is the beta function,
$B(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}):=\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FD})/\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})$
is the beta function,
![]() $\unicode[STIX]{x1D701}$
is defined by
$\unicode[STIX]{x1D701}$
is defined by
![]() $\unicode[STIX]{x1D70E}(y)=\unicode[STIX]{x1D701}y$
and we put
$\unicode[STIX]{x1D70E}(y)=\unicode[STIX]{x1D701}y$
and we put
This shows that the monodromy on the 2-dimensional
![]() $H_{1}(X_{t},\mathbb{C})(\unicode[STIX]{x1D712})$
is isomorphic to the monodromy of the hypergeometric equation
$H_{1}(X_{t},\mathbb{C})(\unicode[STIX]{x1D712})$
is isomorphic to the monodromy of the hypergeometric equation
with the Riemann scheme
 $$\begin{eqnarray}\left\{\begin{array}{@{}ccc@{}}t=0 & t=1 & t=\infty \\ 0 & 0 & \unicode[STIX]{x1D6FC}_{n}\\ 1-\unicode[STIX]{x1D6FC}_{n}-\unicode[STIX]{x1D6FD}_{n} & 0 & \unicode[STIX]{x1D6FD}_{n}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ccc@{}}t=0 & t=1 & t=\infty \\ 0 & 0 & \unicode[STIX]{x1D6FC}_{n}\\ 1-\unicode[STIX]{x1D6FC}_{n}-\unicode[STIX]{x1D6FD}_{n} & 0 & \unicode[STIX]{x1D6FD}_{n}\end{array}\right\}\end{eqnarray}$$
In particular, the monodromy is irreducible as
![]() $\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n}\not \in \mathbb{Z}$
.
$\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n}\not \in \mathbb{Z}$
.
3.3 Hodge numbers
Let
![]() $f:X\rightarrow \mathbb{P}^{1}$
be a HG fibration with multiplication by
$f:X\rightarrow \mathbb{P}^{1}$
be a HG fibration with multiplication by
![]() $(R_{0},e_{0})$
. Following [Reference Asakura and Otsubo3, Section 4.1], we consider motivic sheaves
$(R_{0},e_{0})$
. Following [Reference Asakura and Otsubo3, Section 4.1], we consider motivic sheaves
![]() $\mathscr{M}$
and
$\mathscr{M}$
and
![]() $\mathscr{H}$
which are defined in the following way. Let
$\mathscr{H}$
which are defined in the following way. Let
![]() $S:=\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}$
be defined over
$S:=\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}$
be defined over
![]() $\overline{\mathbb{Q}}$
with coordinate
$\overline{\mathbb{Q}}$
with coordinate
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $\mathbb{P}_{S}^{1}:=\mathbb{P}^{1}\times S$
and denote the coordinates by
$\mathbb{P}_{S}^{1}:=\mathbb{P}^{1}\times S$
and denote the coordinates by
![]() $(t,\unicode[STIX]{x1D706})$
. Put
$(t,\unicode[STIX]{x1D706})$
. Put
![]() $\mathbb{P}_{S}^{1}\supset \mathscr{U}:=(\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}\times S)\setminus \unicode[STIX]{x1D6E5}$
where
$\mathbb{P}_{S}^{1}\supset \mathscr{U}:=(\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}\times S)\setminus \unicode[STIX]{x1D6E5}$
where
![]() $\unicode[STIX]{x1D6E5}$
is the diagonal subscheme. Let
$\unicode[STIX]{x1D6E5}$
is the diagonal subscheme. Let
![]() $l\geqslant 1$
be an integer. Let
$l\geqslant 1$
be an integer. Let
![]() $\unicode[STIX]{x1D70B}:\mathbb{P}_{S}^{1}\rightarrow \mathbb{P}_{S}^{1}$
be a morphism over
$\unicode[STIX]{x1D70B}:\mathbb{P}_{S}^{1}\rightarrow \mathbb{P}_{S}^{1}$
be a morphism over
![]() $S$
given by
$S$
given by
![]() $(t,\unicode[STIX]{x1D706})\mapsto (\unicode[STIX]{x1D706}-t^{l},\unicode[STIX]{x1D706})$
. Then we define
$(t,\unicode[STIX]{x1D706})\mapsto (\unicode[STIX]{x1D706}-t^{l},\unicode[STIX]{x1D706})$
. Then we define
a variation of Hodge–de Rham structures (VHdR) on
![]() $\mathscr{U}$
and
$\mathscr{U}$
and
a variation of mixed Hodge–de Rham structures (VMHdR) on
![]() $S$
, where the terminology is as in [Reference Asakura and Otsubo3, Section 2.1] or [Reference Asakura and Otsubo4, Section 2.1]. For the reader’s convenience, we give a description of the stalk
$S$
, where the terminology is as in [Reference Asakura and Otsubo3, Section 2.1] or [Reference Asakura and Otsubo4, Section 2.1]. For the reader’s convenience, we give a description of the stalk
![]() $H_{a}=\mathscr{H}|_{\{a\}}$
and
$H_{a}=\mathscr{H}|_{\{a\}}$
and
![]() $\mathscr{M}_{a}=\mathscr{M}|_{\text{pr}_{2}^{-1}(a)}=\mathscr{M}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}$
at
$\mathscr{M}_{a}=\mathscr{M}|_{\text{pr}_{2}^{-1}(a)}=\mathscr{M}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}$
at
![]() $a\in S$
is given in the following way. Let
$a\in S$
is given in the following way. Let
![]() $\unicode[STIX]{x1D70B}_{a}:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
be the map given by
$\unicode[STIX]{x1D70B}_{a}:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
be the map given by
![]() $t\mapsto a-t^{l}$
. Let
$t\mapsto a-t^{l}$
. Let

be a Cartesian diagram, and
![]() $i$
a desingularization along the singular fibers. Put
$i$
a desingularization along the singular fibers. Put
![]() $U_{a}:=\unicode[STIX]{x1D70B}_{a}^{-1}(\mathbb{A}^{1}\setminus \{0,1,a\})$
. Then
$U_{a}:=\unicode[STIX]{x1D70B}_{a}^{-1}(\mathbb{A}^{1}\setminus \{0,1,a\})$
. Then
 $$\begin{eqnarray}\displaystyle \mathscr{M}_{a} & = & \displaystyle \unicode[STIX]{x1D70B}_{a\ast }\mathbb{Q}\otimes R^{1}f_{\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}=\unicode[STIX]{x1D70B}_{a\ast }\unicode[STIX]{x1D70B}_{a}^{\ast }R^{1}f_{\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{a\ast }R^{1}f_{a\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}},\nonumber\\ \displaystyle H_{a} & = & \displaystyle H^{1}(\mathbb{A}^{1}\setminus \{0,1,a\},\mathscr{M}_{a})\nonumber\\ \displaystyle & \cong & \displaystyle H^{1}(U_{a},R^{1}f_{a\ast }\mathbb{Q})\subset H^{2}(f_{a}^{-1}(U_{a}),\mathbb{Q}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{M}_{a} & = & \displaystyle \unicode[STIX]{x1D70B}_{a\ast }\mathbb{Q}\otimes R^{1}f_{\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}=\unicode[STIX]{x1D70B}_{a\ast }\unicode[STIX]{x1D70B}_{a}^{\ast }R^{1}f_{\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D70B}_{a\ast }R^{1}f_{a\ast }\mathbb{Q}|_{\mathbb{A}^{1}\setminus \{0,1,a\}},\nonumber\\ \displaystyle H_{a} & = & \displaystyle H^{1}(\mathbb{A}^{1}\setminus \{0,1,a\},\mathscr{M}_{a})\nonumber\\ \displaystyle & \cong & \displaystyle H^{1}(U_{a},R^{1}f_{a\ast }\mathbb{Q})\subset H^{2}(f_{a}^{-1}(U_{a}),\mathbb{Q}).\end{eqnarray}$$
The weights of
![]() $\mathscr{H}$
are at most
$\mathscr{H}$
are at most
![]() $2,3,4$
, and hence there is an exact sequence
$2,3,4$
, and hence there is an exact sequence
of VMHdR structures on
![]() $S$
. By (3.6), there is a canonical surjective map
$S$
. By (3.6), there is a canonical surjective map
where we put
![]() $H^{2}(X_{a},\mathbb{Q})_{0}:=\text{Ker}[H^{2}(X_{a},\mathbb{Q})\rightarrow H^{2}(f_{a}^{-1}(t),\mathbb{Q})]$
,
$H^{2}(X_{a},\mathbb{Q})_{0}:=\text{Ker}[H^{2}(X_{a},\mathbb{Q})\rightarrow H^{2}(f_{a}^{-1}(t),\mathbb{Q})]$
,
![]() $t\in U_{a}$
.
$t\in U_{a}$
.
Let
![]() $\unicode[STIX]{x1D707}_{l}$
be the group of
$\unicode[STIX]{x1D707}_{l}$
be the group of
![]() $l$
th roots of unity which acts on
$l$
th roots of unity which acts on
![]() $\unicode[STIX]{x1D70B}_{\ast }\mathbb{Q}$
in a natural way. Then
$\unicode[STIX]{x1D70B}_{\ast }\mathbb{Q}$
in a natural way. Then
![]() $\mathscr{M}$
has multiplication by the group ring
$\mathscr{M}$
has multiplication by the group ring
![]() $R:=R_{0}[\unicode[STIX]{x1D707}_{l}]$
. Let
$R:=R_{0}[\unicode[STIX]{x1D707}_{l}]$
. Let
![]() $e:R\rightarrow E$
be a projection onto a number field
$e:R\rightarrow E$
be a projection onto a number field
![]() $E$
such that
$E$
such that
![]() $\text{Ker}(e)\supset \text{Ker}(e_{0})$
. There is a unique embedding
$\text{Ker}(e)\supset \text{Ker}(e_{0})$
. There is a unique embedding
![]() $E_{0}{\hookrightarrow}E$
making the diagram
$E_{0}{\hookrightarrow}E$
making the diagram

commutative.
For
![]() $\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
factoring through
$\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
factoring through
![]() $e$
, we denote by
$e$
, we denote by
![]() $V(\unicode[STIX]{x1D712})$
the
$V(\unicode[STIX]{x1D712})$
the
![]() $\unicode[STIX]{x1D712}$
-part which is defined to be the subspace on which
$\unicode[STIX]{x1D712}$
-part which is defined to be the subspace on which
![]() $r\in R$
acts as multiplication by
$r\in R$
acts as multiplication by
![]() $\unicode[STIX]{x1D712}(r)$
.
$\unicode[STIX]{x1D712}(r)$
.
Theorem 3.3. Let
![]() $T_{p}$
denote the local monodromy on
$T_{p}$
denote the local monodromy on
![]() $R^{1}f_{\ast }\overline{\mathbb{Q}}(\unicode[STIX]{x1D712})$
at
$R^{1}f_{\ast }\overline{\mathbb{Q}}(\unicode[STIX]{x1D712})$
at
![]() $t=p$
. Let
$t=p$
. Let
![]() $\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}$
(resp.
$\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}$
(resp.
![]() $\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
) for
$\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
) for
![]() $j=1,2$
be rational numbers such that
$j=1,2$
be rational numbers such that
![]() $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}}$
(resp.
$e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}}$
(resp.
![]() $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}}$
) are eigenvalues of
$e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}}$
) are eigenvalues of
![]() $T_{0}$
(resp.
$T_{0}$
(resp.
![]() $T_{\infty }$
). Let
$T_{\infty }$
). Let
![]() $k$
be an integer such that
$k$
be an integer such that
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701}_{l})=\unicode[STIX]{x1D701}_{l}^{k}$
for
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701}_{l})=\unicode[STIX]{x1D701}_{l}^{k}$
for
![]() $\unicode[STIX]{x1D701}_{l}\in \unicode[STIX]{x1D707}_{l}$
. Suppose that
$\unicode[STIX]{x1D701}_{l}\in \unicode[STIX]{x1D707}_{l}$
. Suppose that
![]() $k/l,-k/l+\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
and
$k/l,-k/l+\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
and
![]() $\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}\in \mathbb{Z}$
. Write
$\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}\in \mathbb{Z}$
. Write
![]() $h_{\unicode[STIX]{x1D712}}^{p,2-p}:=\dim _{\overline{\mathbb{Q}}}\text{Gr}_{F}^{p}W_{2}\mathscr{H}(\unicode[STIX]{x1D712})$
. Put
$h_{\unicode[STIX]{x1D712}}^{p,2-p}:=\dim _{\overline{\mathbb{Q}}}\text{Gr}_{F}^{p}W_{2}\mathscr{H}(\unicode[STIX]{x1D712})$
. Put
Then
 $$\begin{eqnarray}(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=\left\{\begin{array}{@{}ll@{}}(1,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,2,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,1,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=\left\{\begin{array}{@{}ll@{}}(1,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,2,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,1,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0.\end{array}\right.\end{eqnarray}$$
Note that
![]() $d_{\unicode[STIX]{x1D712}}$
takes values only in
$d_{\unicode[STIX]{x1D712}}$
takes values only in
![]() $0,1$
or
$0,1$
or
![]() $2$
. Indeed
$2$
. Indeed
and each
![]() $\unicode[STIX]{x1D6FF}_{i}$
is either
$\unicode[STIX]{x1D6FF}_{i}$
is either
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Proof. We first note that
![]() $\dim _{E}W_{2}\mathscr{H}(e)=2$
[Reference Asakura and Otsubo3, Section 4.3]. We employ two results from [Reference Asakura and Fresán2] and [Reference Fedorov9], respectively. First of all, it follows from [Reference Asakura and Fresán2, Theorem 4.2] that one has the Hodge numbers of the determinant
$\dim _{E}W_{2}\mathscr{H}(e)=2$
[Reference Asakura and Otsubo3, Section 4.3]. We employ two results from [Reference Asakura and Fresán2] and [Reference Fedorov9], respectively. First of all, it follows from [Reference Asakura and Fresán2, Theorem 4.2] that one has the Hodge numbers of the determinant
![]() $D:=\text{det}_{E}W_{2}\mathscr{H}(e)=\bigwedge _{E}^{2}W_{2}\mathscr{H}(e)$
. The result is
$D:=\text{det}_{E}W_{2}\mathscr{H}(e)=\bigwedge _{E}^{2}W_{2}\mathscr{H}(e)$
. The result is
 $$\begin{eqnarray}(D_{\unicode[STIX]{x1D712}}^{4,0},D_{\unicode[STIX]{x1D712}}^{3,1},D_{\unicode[STIX]{x1D712}}^{2,2},D_{\unicode[STIX]{x1D712}}^{1,3},D_{\unicode[STIX]{x1D712}}^{0,4})=\left\{\begin{array}{@{}ll@{}}(0,1,0,0,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,0,1,0,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,0,0,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(D_{\unicode[STIX]{x1D712}}^{4,0},D_{\unicode[STIX]{x1D712}}^{3,1},D_{\unicode[STIX]{x1D712}}^{2,2},D_{\unicode[STIX]{x1D712}}^{1,3},D_{\unicode[STIX]{x1D712}}^{0,4})=\left\{\begin{array}{@{}ll@{}}(0,1,0,0,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,0,1,0,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,0,0,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0\end{array}\right.\end{eqnarray}$$
where we put
![]() $D_{\unicode[STIX]{x1D712}}^{p,4-p}:=\dim \text{Gr}_{F}^{p}D(\unicode[STIX]{x1D712})$
. Since
$D_{\unicode[STIX]{x1D712}}^{p,4-p}:=\dim \text{Gr}_{F}^{p}D(\unicode[STIX]{x1D712})$
. Since
![]() $D_{\unicode[STIX]{x1D712}}^{p,4-p}=1$
$D_{\unicode[STIX]{x1D712}}^{p,4-p}=1$
![]() $\Leftrightarrow$
$\Leftrightarrow$
![]() $2h_{\unicode[STIX]{x1D712}}^{2,0}+h_{\unicode[STIX]{x1D712}}^{1,1}=p$
, this implies
$2h_{\unicode[STIX]{x1D712}}^{2,0}+h_{\unicode[STIX]{x1D712}}^{1,1}=p$
, this implies
 $$\begin{eqnarray}(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=\left\{\begin{array}{@{}ll@{}}(1,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,2,0)\text{ or }(1,0,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,1,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=\left\{\begin{array}{@{}ll@{}}(1,1,0)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=2,\\ (0,2,0)\text{ or }(1,0,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=1,\\ (0,1,1)\quad & \text{if }d_{\unicode[STIX]{x1D712}}=0\end{array}\right.\end{eqnarray}$$
which completes the proof in the case
![]() $d_{\unicode[STIX]{x1D712}}\neq 1$
. Suppose
$d_{\unicode[STIX]{x1D712}}\neq 1$
. Suppose
![]() $d_{\unicode[STIX]{x1D712}}=1$
. We want to show that
$d_{\unicode[STIX]{x1D712}}=1$
. We want to show that
![]() $(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
cannot happen. By [Reference Asakura and Otsubo3, Theorem 5.8], the underlying connection of
$(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
cannot happen. By [Reference Asakura and Otsubo3, Theorem 5.8], the underlying connection of
![]() $W_{2}\mathscr{H}(\unicode[STIX]{x1D712})$
is defined by the hypergeometric differential operator as in loc. cit. One can apply the main theorem in [Reference Fedorov9] and then the possible triplets of the Hodge numbers are at most
$W_{2}\mathscr{H}(\unicode[STIX]{x1D712})$
is defined by the hypergeometric differential operator as in loc. cit. One can apply the main theorem in [Reference Fedorov9] and then the possible triplets of the Hodge numbers are at most
![]() $(2,0,0),(0,2,0),(0,0,2)$
. In particular, the case
$(2,0,0),(0,2,0),(0,0,2)$
. In particular, the case
![]() $(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
is excluded. This completes the proof in case
$(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
is excluded. This completes the proof in case
![]() $d_{\unicode[STIX]{x1D712}}=1$
.◻
$d_{\unicode[STIX]{x1D712}}=1$
.◻
Remark 3.4. For the latter half of the proof of Theorem 3.3, there is an alternative discussion without using the main theorem of [Reference Fedorov9]. Let
![]() $\unicode[STIX]{x1D70B}_{0}:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
be the map given by
$\unicode[STIX]{x1D70B}_{0}:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$
be the map given by
![]() $t\mapsto -t^{l}$
. Let
$t\mapsto -t^{l}$
. Let
![]() $\mathscr{M}_{0}:=\unicode[STIX]{x1D70B}_{0\ast }\mathbb{Q}\otimes R^{1}f_{\ast }\mathbb{Q}$
be a VHdR on
$\mathscr{M}_{0}:=\unicode[STIX]{x1D70B}_{0\ast }\mathbb{Q}\otimes R^{1}f_{\ast }\mathbb{Q}$
be a VHdR on
![]() $\mathbb{P}^{1}\setminus \{0,1,\infty \}$
. Put
$\mathbb{P}^{1}\setminus \{0,1,\infty \}$
. Put
![]() $H_{0}:=H^{1}(\mathbb{P}^{1}\setminus \{0,1,\infty \},\mathscr{M}_{0})$
. Let
$H_{0}:=H^{1}(\mathbb{P}^{1}\setminus \{0,1,\infty \},\mathscr{M}_{0})$
. Let
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}=0}$
denote the nearby cycle functor. Then one can construct an injection
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D706}=0}$
denote the nearby cycle functor. Then one can construct an injection
of mixed Hodge–de Rham structures. The cohomology group
![]() $W_{2}H_{0}(e)$
is studied in detail in [Reference Asakura and Otsubo4]. In particular, if
$W_{2}H_{0}(e)$
is studied in detail in [Reference Asakura and Otsubo4]. In particular, if
![]() $d_{\unicode[STIX]{x1D712}}=1$
, then the Hodge type of
$d_{\unicode[STIX]{x1D712}}=1$
, then the Hodge type of
![]() $W_{2}H_{0}(\unicode[STIX]{x1D712})$
is
$W_{2}H_{0}(\unicode[STIX]{x1D712})$
is
![]() $(1,1)$
. Hence
$(1,1)$
. Hence
![]() $h_{\unicode[STIX]{x1D712}}^{1,1}>0$
by the above injection, which excludes the case
$h_{\unicode[STIX]{x1D712}}^{1,1}>0$
by the above injection, which excludes the case
![]() $(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
.
$(h_{\unicode[STIX]{x1D712}}^{2,0},h_{\unicode[STIX]{x1D712}}^{1,1},h_{\unicode[STIX]{x1D712}}^{0,2})=(1,0,1)$
.
Corollary 3.5.
![]() $W_{2}\mathscr{H}(e)$
is a Tate VHdR of type
$W_{2}\mathscr{H}(e)$
is a Tate VHdR of type
![]() $(1,1)$
if and only if
$(1,1)$
if and only if
![]() $d_{\unicode[STIX]{x1D712}}=1$
for all
$d_{\unicode[STIX]{x1D712}}=1$
for all
![]() $\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
, equivalently
$\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
, equivalently
for
![]() $\forall s\in \hat{\mathbb{Z}}^{\times }$
where
$\forall s\in \hat{\mathbb{Z}}^{\times }$
where
![]() $\unicode[STIX]{x1D712}_{0}$
is a fixed one and
$\unicode[STIX]{x1D712}_{0}$
is a fixed one and
![]() $\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}_{0}},k_{0}$
are the rational numbers arising from
$\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}_{0}},k_{0}$
are the rational numbers arising from
![]() $\unicode[STIX]{x1D712}_{0}$
.
$\unicode[STIX]{x1D712}_{0}$
.
3.4 Beilinson regulator
Let
![]() $\unicode[STIX]{x1D713}_{t=1}$
be the nearby cycle functor along the function
$\unicode[STIX]{x1D713}_{t=1}$
be the nearby cycle functor along the function
![]() $t-1$
on
$t-1$
on
![]() $\mathscr{U}$
, and put
$\mathscr{U}$
, and put
a VHdR on
![]() $S$
. The condition (c) in Section 3.1 implies that the
$S$
. The condition (c) in Section 3.1 implies that the
![]() $e$
-part
$e$
-part
![]() $C(e)$
is of Hodge type
$C(e)$
is of Hodge type
![]() $(1,1)$
. Recall from [Reference Asakura and Otsubo3, Proposition 4.2] that there is a natural embedding
$(1,1)$
. Recall from [Reference Asakura and Otsubo3, Proposition 4.2] that there is a natural embedding
This gives a 1-extension
of VMHdR with multiplication by
![]() $E$
which is induced from (3.7). Note
$E$
which is induced from (3.7). Note
![]() $C(e)$
is one-dimensional over
$C(e)$
is one-dimensional over
![]() $E$
and endowed with Hodge type
$E$
and endowed with Hodge type
![]() $(1,1)$
by (c) in Section 3.1.
$(1,1)$
by (c) in Section 3.1.
In [Reference Asakura and Otsubo3, Section 5] we discussed the extension data of (3.9). More precisely, let
![]() $\mathscr{O}^{\text{zar}}$
be the Zariski sheaf of polynomial functions (with coefficients in
$\mathscr{O}^{\text{zar}}$
be the Zariski sheaf of polynomial functions (with coefficients in
![]() $\overline{\mathbb{Q}}$
) on
$\overline{\mathbb{Q}}$
) on
![]() $S=\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}$
with coordinate
$S=\mathbb{A}_{\overline{\mathbb{Q}}}^{1}\setminus \{0,1\}$
with coordinate
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $\mathscr{O}^{an}$
be the sheaf of analytic functions on
$\mathscr{O}^{an}$
be the sheaf of analytic functions on
![]() $S^{an}=\mathbb{C}^{an}\setminus \{0,1\}$
. Let
$S^{an}=\mathbb{C}^{an}\setminus \{0,1\}$
. Let
![]() $a:S^{an}\rightarrow S^{\text{zar}}$
be the canonical morphism from the analytic site to the Zariski site. Set
$a:S^{an}\rightarrow S^{\text{zar}}$
be the canonical morphism from the analytic site to the Zariski site. Set
a sheaf on the analytic site
![]() $\mathbb{C}^{an}\setminus \{0,1\}$
where
$\mathbb{C}^{an}\setminus \{0,1\}$
where
![]() $\unicode[STIX]{x1D704}:\mathscr{H}_{B}\rightarrow a^{-1}\mathscr{H}_{\text{dR}}$
is the comparison map. Let
$\unicode[STIX]{x1D704}:\mathscr{H}_{B}\rightarrow a^{-1}\mathscr{H}_{\text{dR}}$
is the comparison map. Let
![]() $h:\widetilde{S}\rightarrow S$
be a generically finite and dominant map such that
$h:\widetilde{S}\rightarrow S$
be a generically finite and dominant map such that
![]() $\sqrt[l]{\unicode[STIX]{x1D706}-1}\in \overline{\mathbb{Q}}(\widetilde{S})$
. Then
$\sqrt[l]{\unicode[STIX]{x1D706}-1}\in \overline{\mathbb{Q}}(\widetilde{S})$
. Then
![]() $h^{\ast }C(e)$
is a direct sum of copies of the constant VHdR
$h^{\ast }C(e)$
is a direct sum of copies of the constant VHdR
![]() $\mathbb{Q}(-1)$
. The connecting homomorphism arising from (3.9) gives a map
$\mathbb{Q}(-1)$
. The connecting homomorphism arising from (3.9) gives a map
to the Yoneda extension group of VMHdR’s on
![]() $S$
where we simply write
$S$
where we simply write
![]() $h^{\ast }C(e)\otimes \mathbb{Q}(1)=\unicode[STIX]{x1D6E4}(\widetilde{S},h^{\ast }C(e)\otimes \mathbb{Q}(1))$
. Combining this with the Carlson isomorphism (cf. [Reference Asakura and Otsubo3, Proposition 2.1]), we have
$h^{\ast }C(e)\otimes \mathbb{Q}(1)=\unicode[STIX]{x1D6E4}(\widetilde{S},h^{\ast }C(e)\otimes \mathbb{Q}(1))$
. Combining this with the Carlson isomorphism (cf. [Reference Asakura and Otsubo3, Proposition 2.1]), we have
A down-to-earth description of
![]() $\unicode[STIX]{x1D70C}$
is the following. Let
$\unicode[STIX]{x1D70C}$
is the following. Let
![]() $x\in h^{\ast }C(e)\otimes \mathbb{Q}(1)$
. Let
$x\in h^{\ast }C(e)\otimes \mathbb{Q}(1)$
. Let
![]() $e_{\text{dR},x}\in \mathscr{H}^{\prime }(e)_{\text{dR}}\otimes \mathbb{Q}(2)$
and
$e_{\text{dR},x}\in \mathscr{H}^{\prime }(e)_{\text{dR}}\otimes \mathbb{Q}(2)$
and
![]() $e_{B,x}\in \mathscr{H}^{\prime }(e)_{B}\otimes \mathbb{Q}(2)$
be liftings of
$e_{B,x}\in \mathscr{H}^{\prime }(e)_{B}\otimes \mathbb{Q}(2)$
be liftings of
![]() $x$
. Then
$x$
. Then
![]() $\unicode[STIX]{x1D70C}(x)=\pm (\unicode[STIX]{x1D704}(e_{B,x})-e_{\text{dR},x})$
(see also [Reference Asakura and Otsubo3, Section 5.2]).
$\unicode[STIX]{x1D70C}(x)=\pm (\unicode[STIX]{x1D704}(e_{B,x})-e_{\text{dR},x})$
(see also [Reference Asakura and Otsubo3, Section 5.2]).
The map
![]() $\unicode[STIX]{x1D70C}$
agrees with the Beilinson regulator map on the motivic cohomology supported on singular fibers up to sign in the following sense. Let
$\unicode[STIX]{x1D70C}$
agrees with the Beilinson regulator map on the motivic cohomology supported on singular fibers up to sign in the following sense. Let
![]() $\widetilde{\unicode[STIX]{x1D70B}}:\mathbb{P}_{\widetilde{S}}^{1}:=\mathbb{P}^{1}\times _{\overline{\mathbb{Q}}}\widetilde{S}\rightarrow \mathbb{P}^{1}$
be given by
$\widetilde{\unicode[STIX]{x1D70B}}:\mathbb{P}_{\widetilde{S}}^{1}:=\mathbb{P}^{1}\times _{\overline{\mathbb{Q}}}\widetilde{S}\rightarrow \mathbb{P}^{1}$
be given by
![]() $(s,\unicode[STIX]{x1D706}^{\prime })\mapsto h(\unicode[STIX]{x1D706}^{\prime })-s^{l}$
. Consider the diagram
$(s,\unicode[STIX]{x1D706}^{\prime })\mapsto h(\unicode[STIX]{x1D706}^{\prime })-s^{l}$
. Consider the diagram

with
![]() $i$
desingularization and
$i$
desingularization and
![]() $p$
the 2nd projection. Let
$p$
the 2nd projection. Let
be the Beilinson regulator map where
![]() $\text{MHM}(\widetilde{S})$
denotes the category of mixed Hodge modules on
$\text{MHM}(\widetilde{S})$
denotes the category of mixed Hodge modules on
![]() $\widetilde{S}$
. There is a canonical surjective map
$\widetilde{S}$
. There is a canonical surjective map
Let
![]() $U_{\widetilde{S}}\subset \mathbb{P}_{\widetilde{S}}^{1}$
be a Zariski open set on which
$U_{\widetilde{S}}\subset \mathbb{P}_{\widetilde{S}}^{1}$
be a Zariski open set on which
![]() $f_{\widetilde{S}}$
is smooth and projective. Put
$f_{\widetilde{S}}$
is smooth and projective. Put
and
![]() $(R^{2}g_{\ast }\mathbb{Q}(2))_{0}:=\text{Ker}[R^{2}g_{\ast }\mathbb{Q}(2)\rightarrow p_{\ast }(R^{2}(f_{\widetilde{S}})_{\ast }\mathbb{Q}(2)|_{U_{\widetilde{S}}})]$
. Then the regulator map induces a map
$(R^{2}g_{\ast }\mathbb{Q}(2))_{0}:=\text{Ker}[R^{2}g_{\ast }\mathbb{Q}(2)\rightarrow p_{\ast }(R^{2}(f_{\widetilde{S}})_{\ast }\mathbb{Q}(2)|_{U_{\widetilde{S}}})]$
. Then the regulator map induces a map
Recall from (3.8) that there is a canonical surjective map
![]() $(R^{2}g_{\ast }\mathbb{Q}(2))_{0}\rightarrow h^{\ast }W_{2}\mathscr{H}(2)$
. We thus have a composition
$(R^{2}g_{\ast }\mathbb{Q}(2))_{0}\rightarrow h^{\ast }W_{2}\mathscr{H}(2)$
. We thus have a composition
of the maps. The compatibility with (3.10) is given by the commutate diagram

where
![]() $D_{\widetilde{S}}:=X_{\widetilde{S}}\setminus U_{\widetilde{S}}$
.
$D_{\widetilde{S}}:=X_{\widetilde{S}}\setminus U_{\widetilde{S}}$
.
3.5 Regulator formula for HG fibrations of Gauss type
One of the main results in [Reference Asakura and Otsubo3] (which we call regulator formula) is an explicit description of the map
![]() $\unicode[STIX]{x1D70C}$
in (3.10). Here we apply [Reference Asakura and Otsubo3, Theorem 5.9] (=a precise version of regulator formula) to the case that
$\unicode[STIX]{x1D70C}$
in (3.10). Here we apply [Reference Asakura and Otsubo3, Theorem 5.9] (=a precise version of regulator formula) to the case that
![]() $f$
is a HG fibration of Gauss type (see Definition 3.2).
$f$
is a HG fibration of Gauss type (see Definition 3.2).
Let
![]() $f:X\rightarrow \mathbb{P}^{1}$
be a HG fibration of Gauss type with multiplication by
$f:X\rightarrow \mathbb{P}^{1}$
be a HG fibration of Gauss type with multiplication by
![]() $(R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}],e_{0})$
as in Definition 3.2. Let
$(R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}],e_{0})$
as in Definition 3.2. Let
![]() $\unicode[STIX]{x1D712}:E_{0}\rightarrow \overline{\mathbb{Q}}$
be a homomorphism such that
$\unicode[STIX]{x1D712}:E_{0}\rightarrow \overline{\mathbb{Q}}$
be a homomorphism such that
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
. Recall from Section 3.2 that
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
. Recall from Section 3.2 that
![]() $F^{1}H_{\text{dR}}^{1}(X_{t})(\unicode[STIX]{x1D712})$
is one-dimensional and spanned by a 1-form
$F^{1}H_{\text{dR}}^{1}(X_{t})(\unicode[STIX]{x1D712})$
is one-dimensional and spanned by a 1-form
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D714}_{n}:={\displaystyle \frac{x^{a_{n}}(1-x)^{b_{n}}(1-tx)^{c_{n}}}{y^{n}}}\,dx, & \displaystyle \nonumber\\ \displaystyle & a_{n}:=\left\lfloor {\displaystyle \frac{an}{N}}\right\rfloor ,\qquad b_{n}:=\left\lfloor {\displaystyle \frac{bn}{N}}\right\rfloor ,\qquad c_{n}:=\left\lfloor {\displaystyle \frac{Nn-bn}{N}}\right\rfloor =n-b_{n}-1, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D714}_{n}:={\displaystyle \frac{x^{a_{n}}(1-x)^{b_{n}}(1-tx)^{c_{n}}}{y^{n}}}\,dx, & \displaystyle \nonumber\\ \displaystyle & a_{n}:=\left\lfloor {\displaystyle \frac{an}{N}}\right\rfloor ,\qquad b_{n}:=\left\lfloor {\displaystyle \frac{bn}{N}}\right\rfloor ,\qquad c_{n}:=\left\lfloor {\displaystyle \frac{Nn-bn}{N}}\right\rfloor =n-b_{n}-1, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $n\in \{1,2,\ldots ,N-1\}$
such that
$n\in \{1,2,\ldots ,N-1\}$
such that
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
for
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{-n}$
for
![]() $\forall \unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
.
$\forall \unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{N}$
.
Lemma 3.6. Let
![]() $D_{0},D_{1}$
be the reduced singular fibers over
$D_{0},D_{1}$
be the reduced singular fibers over
![]() $t=0,1$
. We assume that
$t=0,1$
. We assume that
![]() $D_{0}+D_{1}$
is a normal crossing divisor (abbreviated NCD). Then
$D_{0}+D_{1}$
is a normal crossing divisor (abbreviated NCD). Then
![]() $t\unicode[STIX]{x1D714}_{n}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{1}\setminus \{\infty \},f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D_{0}+D_{1}))$
.
$t\unicode[STIX]{x1D714}_{n}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{1}\setminus \{\infty \},f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D_{0}+D_{1}))$
.
Proof. Put
![]() $S=\mathbb{P}^{1}\setminus \{0,1,\infty \}$
and
$S=\mathbb{P}^{1}\setminus \{0,1,\infty \}$
and
![]() $U=f^{-1}(S)$
. Let
$U=f^{-1}(S)$
. Let
![]() $\mathscr{V}:=H_{\text{dR}}^{1}(U/S)$
be the bundle and
$\mathscr{V}:=H_{\text{dR}}^{1}(U/S)$
be the bundle and
![]() $\unicode[STIX]{x1D6FB}:\mathscr{V}\rightarrow \unicode[STIX]{x1D6FA}_{S}^{1}\otimes \mathscr{V}$
the Gauss–Manin connection. Let
$\unicode[STIX]{x1D6FB}:\mathscr{V}\rightarrow \unicode[STIX]{x1D6FA}_{S}^{1}\otimes \mathscr{V}$
the Gauss–Manin connection. Let
![]() $D_{\infty }$
be the reduced singular fibers over
$D_{\infty }$
be the reduced singular fibers over
![]() $t=\infty$
and assume that it is a NCD. Put
$t=\infty$
and assume that it is a NCD. Put
![]() $T:=\{0,1,\infty \}$
. Recall that the sheaf
$T:=\{0,1,\infty \}$
. Recall that the sheaf
![]() $\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D)$
(
$\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D)$
(
![]() $D:=D_{0}+D_{1}+D_{\infty }$
) is defined by the exact sequence
$D:=D_{0}+D_{1}+D_{\infty }$
) is defined by the exact sequence
Let
![]() $\mathscr{V}_{e}$
be Deligne’s canonical extension over
$\mathscr{V}_{e}$
be Deligne’s canonical extension over
![]() $\mathbb{P}^{1}$
. This is characterized as the subbundle
$\mathbb{P}^{1}$
. This is characterized as the subbundle
![]() $\mathscr{V}_{e}\subset j_{\ast }\mathscr{V}$
(
$\mathscr{V}_{e}\subset j_{\ast }\mathscr{V}$
(
![]() $j:S{\hookrightarrow}\mathbb{P}^{1}$
) which satisfies
$j:S{\hookrightarrow}\mathbb{P}^{1}$
) which satisfies
∙
 $\unicode[STIX]{x1D6FB}$
has at most log poles,
$\unicode[STIX]{x1D6FB}$
has at most log poles,
 $\unicode[STIX]{x1D6FB}:\mathscr{V}_{e}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{P}^{1}}^{1}(\log (0+1+\infty ))\otimes \mathscr{V}_{e}$
,
$\unicode[STIX]{x1D6FB}:\mathscr{V}_{e}\rightarrow \unicode[STIX]{x1D6FA}_{\mathbb{P}^{1}}^{1}(\log (0+1+\infty ))\otimes \mathscr{V}_{e}$
,∙ The eigenvalues of residue
 $\text{Res}(\unicode[STIX]{x1D6FB})$
at
$\text{Res}(\unicode[STIX]{x1D6FB})$
at
 $t=0,1,\infty$
belong to
$t=0,1,\infty$
belong to
 $[0,1)$
.
$[0,1)$
.
Then there is an isomorphism
[Reference Steenbrink12, 2.20] and
![]() $F^{1}\mathscr{V}_{e}:=\mathscr{V}_{e}\cap j_{\ast }F^{1}\mathscr{V}\cong f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D)$
(loc. cit. 4.20 (ii)). Hence the desired assertion is equivalent to
$F^{1}\mathscr{V}_{e}:=\mathscr{V}_{e}\cap j_{\ast }F^{1}\mathscr{V}\cong f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D)$
(loc. cit. 4.20 (ii)). Hence the desired assertion is equivalent to
To show this, we give a local frame of
![]() $\mathscr{V}_{e}$
at
$\mathscr{V}_{e}$
at
![]() $t=0,1$
explicitly. Let
$t=0,1$
explicitly. Let
and put
Recall from (3.2) a homology cycle
![]() $\unicode[STIX]{x1D6FF}:=(1-\unicode[STIX]{x1D70E}^{d_{1}})(1-\unicode[STIX]{x1D70E}^{d_{2}})u\in H_{1}(X_{t},\mathbb{Z})$
. Then
$\unicode[STIX]{x1D6FF}:=(1-\unicode[STIX]{x1D70E}^{d_{1}})(1-\unicode[STIX]{x1D70E}^{d_{2}})u\in H_{1}(X_{t},\mathbb{Z})$
. Then
This shows that
![]() $\unicode[STIX]{x1D714}_{n}$
and
$\unicode[STIX]{x1D714}_{n}$
and
![]() $\unicode[STIX]{x1D702}_{n}$
are basis of the
$\unicode[STIX]{x1D702}_{n}$
are basis of the
![]() $\unicode[STIX]{x1D712}$
-part
$\unicode[STIX]{x1D712}$
-part
![]() $\mathscr{V}(\unicode[STIX]{x1D712})$
of the bundle (over a Zariski open set of
$\mathscr{V}(\unicode[STIX]{x1D712})$
of the bundle (over a Zariski open set of
![]() $\mathbb{P}^{1}\setminus \{0,1,\infty \}$
). Denote by
$\mathbb{P}^{1}\setminus \{0,1,\infty \}$
). Denote by
![]() $\mathscr{V}(\unicode[STIX]{x1D712})^{\ast }$
the dual connection, and by
$\mathscr{V}(\unicode[STIX]{x1D712})^{\ast }$
the dual connection, and by
![]() $\{\unicode[STIX]{x1D714}_{n}^{\ast },\unicode[STIX]{x1D702}_{n}^{\ast }\}$
the dual basis. Then
$\{\unicode[STIX]{x1D714}_{n}^{\ast },\unicode[STIX]{x1D702}_{n}^{\ast }\}$
the dual basis. Then
is annihilated by the dual connection, and hence
Now (3.13)–(3.15) together with the formulas
 $$\begin{eqnarray}\displaystyle & & \displaystyle t\frac{d}{dt}_{2}F_{1}(a,b,a+b+1;t)\nonumber\\ \displaystyle & & \displaystyle \quad =(a+b)(\,_{2}F_{1}(a,b,a+b;t)-_{2}F_{1}(a,b,a+b+1;t))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle t\frac{d}{dt}_{2}F_{1}(a,b,a+b+1;t)\nonumber\\ \displaystyle & & \displaystyle \quad =(a+b)(\,_{2}F_{1}(a,b,a+b;t)-_{2}F_{1}(a,b,a+b+1;t))\nonumber\end{eqnarray}$$
imply
 $$\begin{eqnarray}\displaystyle & (\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D714}_{n}^{\ast }),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D702}_{n}^{\ast }))=dt\otimes (\unicode[STIX]{x1D714}_{n}^{\ast },\unicode[STIX]{x1D702}_{n}^{\ast })\left(\begin{array}{@{}cc@{}}0 & -\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}/(1-t)\\ -\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}/t & (\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})/t\end{array}\right) & \displaystyle \nonumber\\ \displaystyle & \Longleftrightarrow \quad (\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D714}_{n}),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D702}_{n}))=dt\otimes (\unicode[STIX]{x1D714}_{n},\unicode[STIX]{x1D702}_{n})\left(\begin{array}{@{}cc@{}}0 & \unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}/t\\ \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}/(1-t) & -(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})/t\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & (\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D714}_{n}^{\ast }),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D702}_{n}^{\ast }))=dt\otimes (\unicode[STIX]{x1D714}_{n}^{\ast },\unicode[STIX]{x1D702}_{n}^{\ast })\left(\begin{array}{@{}cc@{}}0 & -\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}/(1-t)\\ -\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}/t & (\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})/t\end{array}\right) & \displaystyle \nonumber\\ \displaystyle & \Longleftrightarrow \quad (\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D714}_{n}),\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D702}_{n}))=dt\otimes (\unicode[STIX]{x1D714}_{n},\unicode[STIX]{x1D702}_{n})\left(\begin{array}{@{}cc@{}}0 & \unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}/t\\ \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}/(1-t) & -(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})/t\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
Then it is an elementary linear algebra to compute local frames of
![]() $\mathscr{V}_{e}$
:
$\mathscr{V}_{e}$
:
 $$\begin{eqnarray}\displaystyle & \mathscr{V}_{e}(\unicode[STIX]{x1D712})|_{t=0}=\left\{\begin{array}{@{}ll@{}}\langle \unicode[STIX]{x1D714}_{n},t(\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D714}_{n}+(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}})\unicode[STIX]{x1D702}_{n})\rangle \quad & \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\leqslant 1,\\ \langle t\unicode[STIX]{x1D714}_{n},(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}-1)\unicode[STIX]{x1D714}_{n}+t\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D702}_{n}\rangle \quad & \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}>1,\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \mathscr{V}_{e}(\unicode[STIX]{x1D712})|_{t=1}=\langle \unicode[STIX]{x1D714}_{n},\unicode[STIX]{x1D702}_{n}\rangle . & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathscr{V}_{e}(\unicode[STIX]{x1D712})|_{t=0}=\left\{\begin{array}{@{}ll@{}}\langle \unicode[STIX]{x1D714}_{n},t(\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D714}_{n}+(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}})\unicode[STIX]{x1D702}_{n})\rangle \quad & \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\leqslant 1,\\ \langle t\unicode[STIX]{x1D714}_{n},(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}-1)\unicode[STIX]{x1D714}_{n}+t\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D702}_{n}\rangle \quad & \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}>1,\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \mathscr{V}_{e}(\unicode[STIX]{x1D712})|_{t=1}=\langle \unicode[STIX]{x1D714}_{n},\unicode[STIX]{x1D702}_{n}\rangle . & \displaystyle \nonumber\end{eqnarray}$$
Now (3.12) is immediate.◻
Let
![]() $e_{0}:\unicode[STIX]{x1D707}_{N}\rightarrow E_{0}^{\times }$
be an injective homomorphism. Then the condition in Lemma 3.1 is satisfied. Let
$e_{0}:\unicode[STIX]{x1D707}_{N}\rightarrow E_{0}^{\times }$
be an injective homomorphism. Then the condition in Lemma 3.1 is satisfied. Let
![]() $e:R:=\mathbb{Q}[\unicode[STIX]{x1D707}_{l},\unicode[STIX]{x1D707}_{N}]\rightarrow E$
be a projection such that
$e:R:=\mathbb{Q}[\unicode[STIX]{x1D707}_{l},\unicode[STIX]{x1D707}_{N}]\rightarrow E$
be a projection such that
![]() $\text{Ker}(e)\supset \text{Ker}(e_{0})$
. Let
$\text{Ker}(e)\supset \text{Ker}(e_{0})$
. Let
![]() $\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
be a homomorphism factoring through
$\unicode[STIX]{x1D712}:R\rightarrow \overline{\mathbb{Q}}$
be a homomorphism factoring through
![]() $e$
. Fix integers
$e$
. Fix integers
![]() $k,n$
such that
$k,n$
such that
Note
![]() $\text{gcd}(n,N)=1$
as
$\text{gcd}(n,N)=1$
as
![]() $e_{0}:\unicode[STIX]{x1D707}_{N}\rightarrow E_{0}^{\times }$
is injective. Let
$e_{0}:\unicode[STIX]{x1D707}_{N}\rightarrow E_{0}^{\times }$
is injective. Let
which do not depend on the choice of
![]() $n$
. Then
$n$
. Then
![]() $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}}$
(resp.
$e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{j}^{\unicode[STIX]{x1D712}}}$
(resp.
![]() $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}}$
) are eigenvalues of the local monodromy
$e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}}$
) are eigenvalues of the local monodromy
![]() $T_{0}$
at
$T_{0}$
at
![]() $t=0$
(resp.
$t=0$
(resp.
![]() $T_{\infty }$
at
$T_{\infty }$
at
![]() $t=\infty$
) on
$t=\infty$
) on
![]() $R^{1}f_{\ast }\mathbb{C}(\unicode[STIX]{x1D712})\cong \mathbb{C}^{2}$
(see (3.5)). The relative 1-form
$R^{1}f_{\ast }\mathbb{C}(\unicode[STIX]{x1D712})\cong \mathbb{C}^{2}$
(see (3.5)). The relative 1-form
![]() $\unicode[STIX]{x1D714}:=t\unicode[STIX]{x1D714}_{n}$
satisfies the conditions (P1), (P2) in [Reference Asakura and Otsubo3, Section 4.5]:
$\unicode[STIX]{x1D714}:=t\unicode[STIX]{x1D714}_{n}$
satisfies the conditions (P1), (P2) in [Reference Asakura and Otsubo3, Section 4.5]:
(P1)
 $\int _{\unicode[STIX]{x1D6FE}_{t}}\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FE}_{t}\in H_{1}(X_{t}))$
is spanned by
$\int _{\unicode[STIX]{x1D6FE}_{t}}\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FE}_{t}\in H_{1}(X_{t}))$
is spanned by
 $t_{2}F_{1}(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},1;1-t)$
and
$t_{2}F_{1}(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},1;1-t)$
and
 $t_{2}F_{1}(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}};t)$
. (This follows from (3.4).)
$t_{2}F_{1}(\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}};t)$
. (This follows from (3.4).)(P2)
 $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{1}\setminus \{\infty \},f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D))$
. (This is Lemma 3.6.)
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6E4}(\mathbb{P}^{1}\setminus \{\infty \},f_{\ast }\unicode[STIX]{x1D6FA}_{X/\mathbb{P}^{1}}^{1}(\log D))$
. (This is Lemma 3.6.)
We thus can apply the regulator formula [Reference Asakura and Otsubo3, Theorem 5.9]. In our particular case, it is stated as follows (the notation is slightly changed for the use in below).
Theorem 3.7. Let
![]() $e_{0},e,\unicode[STIX]{x1D712}$
be as above, and let
$e_{0},e,\unicode[STIX]{x1D712}$
be as above, and let
![]() $\unicode[STIX]{x1D6FC}_{i}^{\unicode[STIX]{x1D712}}$
,
$\unicode[STIX]{x1D6FC}_{i}^{\unicode[STIX]{x1D712}}$
,
![]() $\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
be as in (3.16). Assume that
$\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
be as in (3.16). Assume that
![]() $k/l,k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
. Put
$k/l,k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
. Put
 $$\begin{eqnarray}\displaystyle \mathscr{F}_{1}(\unicode[STIX]{x1D706}) & := & \displaystyle (1-\unicode[STIX]{x1D706})^{k/l-1}~_{3}F_{2}{1,1,1-k/l\atop 2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}};(1-\unicode[STIX]{x1D706})^{-1},\nonumber\\ \displaystyle \mathscr{F}_{2}(\unicode[STIX]{x1D706}) & := & \displaystyle (1-\unicode[STIX]{x1D706})^{k/l-1}~_{3}F_{2}{1,1,2-k/l\atop 2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}};(1-\unicode[STIX]{x1D706})^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{F}_{1}(\unicode[STIX]{x1D706}) & := & \displaystyle (1-\unicode[STIX]{x1D706})^{k/l-1}~_{3}F_{2}{1,1,1-k/l\atop 2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}};(1-\unicode[STIX]{x1D706})^{-1},\nonumber\\ \displaystyle \mathscr{F}_{2}(\unicode[STIX]{x1D706}) & := & \displaystyle (1-\unicode[STIX]{x1D706})^{k/l-1}~_{3}F_{2}{1,1,2-k/l\atop 2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}};(1-\unicode[STIX]{x1D706})^{-1}.\nonumber\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70C}(\!\,^{t}\unicode[STIX]{x1D712})$
be the
$\unicode[STIX]{x1D70C}(\!\,^{t}\unicode[STIX]{x1D712})$
be the
![]() $^{t}\unicode[STIX]{x1D712}$
-part of the map
$^{t}\unicode[STIX]{x1D712}$
-part of the map
![]() $\unicode[STIX]{x1D70C}$
in (3.10). Let
$\unicode[STIX]{x1D70C}$
in (3.10). Let
be a local lifting where the above isomorphism is with respect to
![]() $\overline{\mathbb{Q}}$
-frame of
$\overline{\mathbb{Q}}$
-frame of
![]() $W_{2}\mathscr{H}_{\text{dR}}(\!\,^{t}\unicode[STIX]{x1D712})$
. Define rational functions
$W_{2}\mathscr{H}_{\text{dR}}(\!\,^{t}\unicode[STIX]{x1D712})$
. Define rational functions
![]() $E_{i}^{(r)}=E_{i}^{(r)}(\unicode[STIX]{x1D706})\in \mathbb{Q}(\unicode[STIX]{x1D706})$
for
$E_{i}^{(r)}=E_{i}^{(r)}(\unicode[STIX]{x1D706})\in \mathbb{Q}(\unicode[STIX]{x1D706})$
for
![]() $r\in \mathbb{Z}_{{\geqslant}-1}$
in the following way. Write
$r\in \mathbb{Z}_{{\geqslant}-1}$
in the following way. Write
![]() $a:=2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}$
,
$a:=2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}$
,
![]() $b:=2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}$
. Put
$b:=2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}$
. Put
 $$\begin{eqnarray}\displaystyle & & \displaystyle A(s):=\frac{s(a+b+2s-3-s(1-\unicode[STIX]{x1D706})^{-1})}{(a+s-1)(b+s-1)},\nonumber\\ \displaystyle & & \displaystyle \qquad B(s):=\frac{s(1-s)(1-(1-\unicode[STIX]{x1D706})^{-1})}{(a+s-1)(b+s-1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle A(s):=\frac{s(a+b+2s-3-s(1-\unicode[STIX]{x1D706})^{-1})}{(a+s-1)(b+s-1)},\nonumber\\ \displaystyle & & \displaystyle \qquad B(s):=\frac{s(1-s)(1-(1-\unicode[STIX]{x1D706})^{-1})}{(a+s-1)(b+s-1)}.\nonumber\end{eqnarray}$$
Define
![]() $C_{i}(s)$
and
$C_{i}(s)$
and
![]() $D_{i}(s)$
by
$D_{i}(s)$
by
and define
![]() $E_{i}^{(r)}$
by
$E_{i}^{(r)}$
by
Then for infinitely many integers
![]() $r>0$
, we have
$r>0$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D706}) & \equiv & \displaystyle C_{1}(1-\unicode[STIX]{x1D706})^{r}[E_{1}^{(r)}(\unicode[STIX]{x1D706})\mathscr{F}_{1}(\unicode[STIX]{x1D706})+E_{2}^{(r)}(\unicode[STIX]{x1D706})\mathscr{F}_{2}(\unicode[STIX]{x1D706})],\nonumber\\ \displaystyle \unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D706}) & \equiv & \displaystyle C_{2}(1-\unicode[STIX]{x1D706})^{r-1}[E_{1}^{(r-1)}(\unicode[STIX]{x1D706})\mathscr{F}_{1}(\unicode[STIX]{x1D706})+E_{2}^{(r-1)}(\unicode[STIX]{x1D706})\mathscr{F}_{2}(\unicode[STIX]{x1D706})]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D706}) & \equiv & \displaystyle C_{1}(1-\unicode[STIX]{x1D706})^{r}[E_{1}^{(r)}(\unicode[STIX]{x1D706})\mathscr{F}_{1}(\unicode[STIX]{x1D706})+E_{2}^{(r)}(\unicode[STIX]{x1D706})\mathscr{F}_{2}(\unicode[STIX]{x1D706})],\nonumber\\ \displaystyle \unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D706}) & \equiv & \displaystyle C_{2}(1-\unicode[STIX]{x1D706})^{r-1}[E_{1}^{(r-1)}(\unicode[STIX]{x1D706})\mathscr{F}_{1}(\unicode[STIX]{x1D706})+E_{2}^{(r-1)}(\unicode[STIX]{x1D706})\mathscr{F}_{2}(\unicode[STIX]{x1D706})]\nonumber\end{eqnarray}$$
modulo
![]() $\overline{\mathbb{Q}(\unicode[STIX]{x1D706})}$
with some
$\overline{\mathbb{Q}(\unicode[STIX]{x1D706})}$
with some
![]() $C_{1},C_{2}\in \overline{\mathbb{Q}}^{\times }$
.
$C_{1},C_{2}\in \overline{\mathbb{Q}}^{\times }$
.
We note that
![]() $(N,l,k,n,a,b)$
in Theorem 3.7 can run over the set of all 6-tuples of integers satisfying
$(N,l,k,n,a,b)$
in Theorem 3.7 can run over the set of all 6-tuples of integers satisfying
∙
 $0<a,b<N$
,
$0<a,b<N$
,
 $\gcd (N,a,b)=1$
and
$\gcd (N,a,b)=1$
and
 $\gcd (n,N)=1$
,
$\gcd (n,N)=1$
,∙
 $k/l,k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
(see (3.16) for definition of
$k/l,k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},k/l-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
(see (3.16) for definition of
 $\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
).
$\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}$
).
4 Proof of main theorem
We are now in a position to prove Theorem 2.1 (log formula).
There are the following formulas
 $$\begin{eqnarray}\displaystyle (b_{1}-1)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1}-1,b_{2}};x & = & \displaystyle \left(b_{1}-1+x\frac{d}{dx}\right)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!,\nonumber\\ \displaystyle {a_{1}\cdot \,}_{3}F_{2}{a_{1}+1,a_{2},a_{3}\atop b_{1},b_{2}};x & = & \displaystyle \left(a_{1}+x\frac{d}{dx}\right)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (b_{1}-1)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1}-1,b_{2}};x & = & \displaystyle \left(b_{1}-1+x\frac{d}{dx}\right)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!,\nonumber\\ \displaystyle {a_{1}\cdot \,}_{3}F_{2}{a_{1}+1,a_{2},a_{3}\atop b_{1},b_{2}};x & = & \displaystyle \left(a_{1}+x\frac{d}{dx}\right)_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!,\nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle (a_{2}-b_{1})(a_{1}-b_{1})(a_{3}-b_{1})_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1}+1,b_{2}};x & = & \displaystyle \unicode[STIX]{x1D703}_{1}\left(\,_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!\right)\!,\nonumber\\ \displaystyle (a_{1}-b_{1})(a_{1}-b_{2})_{3}F_{2}{a_{1}-1,a_{2},a_{3}\atop b_{1},b_{2}};x & = & \displaystyle \unicode[STIX]{x1D703}_{2}\left(\,_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!\right)\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (a_{2}-b_{1})(a_{1}-b_{1})(a_{3}-b_{1})_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1}+1,b_{2}};x & = & \displaystyle \unicode[STIX]{x1D703}_{1}\left(\,_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!\right)\!,\nonumber\\ \displaystyle (a_{1}-b_{1})(a_{1}-b_{2})_{3}F_{2}{a_{1}-1,a_{2},a_{3}\atop b_{1},b_{2}};x & = & \displaystyle \unicode[STIX]{x1D703}_{2}\left(\,_{3}F_{2}{a_{1},a_{2},a_{3}\atop b_{1},b_{2}};x\!\right)\!,\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{1} & := & \displaystyle -a_{1}a_{2}a_{3}+(a_{2}-b_{1})(a_{1}-b_{1})(a_{3}-b_{1})\nonumber\\ \displaystyle & & \displaystyle +\,b_{1}(b_{2}+(b_{1}-a_{1}-a_{2}-a_{3}-1)x)\frac{d}{dx}+b_{1}(x-x^{2})\frac{d^{2}}{dx^{2}}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{2} & := & \displaystyle (a_{1}-b_{1})(a_{1}-b_{2})-a_{2}a_{3}x\nonumber\\ \displaystyle & & \displaystyle +\,((b_{1}+b_{2}-a_{1})-(a_{2}+a_{3}+1)x)x\frac{d}{dx}+(1-x)x^{2}\frac{d^{2}}{dx^{2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{1} & := & \displaystyle -a_{1}a_{2}a_{3}+(a_{2}-b_{1})(a_{1}-b_{1})(a_{3}-b_{1})\nonumber\\ \displaystyle & & \displaystyle +\,b_{1}(b_{2}+(b_{1}-a_{1}-a_{2}-a_{3}-1)x)\frac{d}{dx}+b_{1}(x-x^{2})\frac{d^{2}}{dx^{2}}\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{2} & := & \displaystyle (a_{1}-b_{1})(a_{1}-b_{2})-a_{2}a_{3}x\nonumber\\ \displaystyle & & \displaystyle +\,((b_{1}+b_{2}-a_{1})-(a_{2}+a_{3}+1)x)x\frac{d}{dx}+(1-x)x^{2}\frac{d^{2}}{dx^{2}}.\nonumber\end{eqnarray}$$
Therefore if one can prove the log formula for
![]() $_{3}F_{2}({1,1,q\atop a,~b};x)$
then one immediately has the log formula for
$_{3}F_{2}({1,1,q\atop a,~b};x)$
then one immediately has the log formula for
![]() $_{3}F_{2}({n_{1},n_{2},q+n_{3}\atop a+n_{4},~b+n_{5}};x)$
for arbitrary integers
$_{3}F_{2}({n_{1},n_{2},q+n_{3}\atop a+n_{4},~b+n_{5}};x)$
for arbitrary integers
![]() $n_{1},n_{2}>0$
and
$n_{1},n_{2}>0$
and
![]() $n_{3},n_{4},n_{5}\in \mathbb{Z}$
.
$n_{3},n_{4},n_{5}\in \mathbb{Z}$
.
We keep the setting and the notation in Section 3.5. Suppose that
Then it follows from Corollary 3.5 that
![]() $W_{2}\mathscr{H}(e)$
is a Tate HdR structure of type
$W_{2}\mathscr{H}(e)$
is a Tate HdR structure of type
![]() $(1,1)$
. Let us look at the map
$(1,1)$
. Let us look at the map
![]() $\unicode[STIX]{x1D70C}(\!\,^{t}\unicode[STIX]{x1D712})$
in Theorem 3.7. This turns out to be the Beilinson regulator by the diagram (3.11). Since
$\unicode[STIX]{x1D70C}(\!\,^{t}\unicode[STIX]{x1D712})$
in Theorem 3.7. This turns out to be the Beilinson regulator by the diagram (3.11). Since
![]() $W_{2}\mathscr{H}(e)$
is Tate, it is generated by the divisor classes of the geometric generic fiber
$W_{2}\mathscr{H}(e)$
is Tate, it is generated by the divisor classes of the geometric generic fiber
![]() $X_{\overline{\unicode[STIX]{x1D702}}}$
of
$X_{\overline{\unicode[STIX]{x1D702}}}$
of
![]() $f_{\widetilde{S}}$
. This implies that the image of
$f_{\widetilde{S}}$
. This implies that the image of
![]() $\text{reg}_{0}$
in (3.11) is generated by the images of
$\text{reg}_{0}$
in (3.11) is generated by the images of
![]() $H_{\mathscr{M}}^{1}(\widetilde{D}_{i},\mathbb{Q}(1))$
where
$H_{\mathscr{M}}^{1}(\widetilde{D}_{i},\mathbb{Q}(1))$
where
![]() $D_{i}$
runs over the generators of the Neron–Severi group
$D_{i}$
runs over the generators of the Neron–Severi group
![]() $\text{NS}(X_{\overline{\unicode[STIX]{x1D702}}})\otimes \mathbb{Q}$
and
$\text{NS}(X_{\overline{\unicode[STIX]{x1D702}}})\otimes \mathbb{Q}$
and
![]() $\widetilde{D}_{i}\rightarrow D_{i}$
is the desingularization. As is well known,
$\widetilde{D}_{i}\rightarrow D_{i}$
is the desingularization. As is well known,
![]() $H_{\mathscr{M}}^{1}(\widetilde{D}_{i},\mathbb{Q}(1))\cong \overline{\unicode[STIX]{x1D702}}^{\times }\otimes \mathbb{Q}$
as
$H_{\mathscr{M}}^{1}(\widetilde{D}_{i},\mathbb{Q}(1))\cong \overline{\unicode[STIX]{x1D702}}^{\times }\otimes \mathbb{Q}$
as
![]() $\widetilde{D}_{i}$
is smooth projective, and the Beilinson regulator on it is given by the logarithmic function. Therefore we have
$\widetilde{D}_{i}$
is smooth projective, and the Beilinson regulator on it is given by the logarithmic function. Therefore we have
We now apply Theorem 3.7. If one can show that
for almost all
![]() $r>0$
, then we have
$r>0$
, then we have
![]() $\mathscr{F}_{i}(\unicode[STIX]{x1D706})\in \overline{\mathbb{Q}(\unicode[STIX]{x1D706})}+\overline{\mathbb{Q}(\unicode[STIX]{x1D706})}\log \overline{\mathbb{Q}(\unicode[STIX]{x1D706})}^{\times }$
, which would finish the proof of Theorem 2.1. To do this, recall (3.17). Letting
$\mathscr{F}_{i}(\unicode[STIX]{x1D706})\in \overline{\mathbb{Q}(\unicode[STIX]{x1D706})}+\overline{\mathbb{Q}(\unicode[STIX]{x1D706})}\log \overline{\mathbb{Q}(\unicode[STIX]{x1D706})}^{\times }$
, which would finish the proof of Theorem 2.1. To do this, recall (3.17). Letting
we want to show
for almost all
![]() $r>0$
. Since
$r>0$
. Since
(4.3) is reduced to showing that
for all integers
![]() $r$
. However, this follows from
$r$
. However, this follows from
 $$\begin{eqnarray}\displaystyle \left|\begin{array}{@{}cc@{}}E_{1}^{(0)}(s) & E_{2}^{(0)}(s)\\ E_{1}^{(-1)}(s) & E_{2}^{(-1)}(s)\end{array}\right| & = & \displaystyle \left|\begin{array}{@{}cc@{}}\unicode[STIX]{x1D706}+(1-\unicode[STIX]{x1D706})A(s) & (1-\unicode[STIX]{x1D706})B(s)\\ 1-\unicode[STIX]{x1D706} & \unicode[STIX]{x1D706}\end{array}\right|\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}\frac{(a-1)(b-1)\unicode[STIX]{x1D706}+s(a+b-2)}{(s+a-1)(s+b-1)},\nonumber\\ \displaystyle & & \displaystyle (a:=2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},b:=2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left|\begin{array}{@{}cc@{}}E_{1}^{(0)}(s) & E_{2}^{(0)}(s)\\ E_{1}^{(-1)}(s) & E_{2}^{(-1)}(s)\end{array}\right| & = & \displaystyle \left|\begin{array}{@{}cc@{}}\unicode[STIX]{x1D706}+(1-\unicode[STIX]{x1D706})A(s) & (1-\unicode[STIX]{x1D706})B(s)\\ 1-\unicode[STIX]{x1D706} & \unicode[STIX]{x1D706}\end{array}\right|\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}\frac{(a-1)(b-1)\unicode[STIX]{x1D706}+s(a+b-2)}{(s+a-1)(s+b-1)},\nonumber\\ \displaystyle & & \displaystyle (a:=2-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},b:=2-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})\nonumber\end{eqnarray}$$
and the fact
![]() $\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
(see (3.16)) and
$\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
(see (3.16)) and
![]() $k/l-\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
as is assumed. This completes the proof of Theorem 2.1.
$k/l-\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$
as is assumed. This completes the proof of Theorem 2.1.
Acknowledgment
This work is supported by JSPS grant-in-aid for Scientific Research: 15K04769 and 25400007.