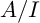1 Introduction
The following problem has a long history in commutative algebra, cf. [Reference Grothendieck8, remarque 7.4.8].
Question 1.1. What properties
![]() $\mathbf {P}$
of rings satisfy the lifting property, that is, for every Noetherian ring A and ideal I of A, if A is I-adically complete and
$\mathbf {P}$
of rings satisfy the lifting property, that is, for every Noetherian ring A and ideal I of A, if A is I-adically complete and
![]() $A/I$
satisfies
$A/I$
satisfies
![]() $\mathbf {P}$
, then A satisfies
$\mathbf {P}$
, then A satisfies
![]() $\mathbf {P}$
.
$\mathbf {P}$
.
There have been numerous studies on the lifting property and its variants, for many important properties
![]() $\mathbf {P}$
. For example, lifting property holds for
$\mathbf {P}$
. For example, lifting property holds for
![]() $\mathbf {P}$
=“Nagata” [Reference Marot18] and
$\mathbf {P}$
=“Nagata” [Reference Marot18] and
![]() $\mathbf {P}$
=“quasi-excellent” [Reference Kurano and Shimomoto15], but not for
$\mathbf {P}$
=“quasi-excellent” [Reference Kurano and Shimomoto15], but not for
![]() $\mathbf {P}$
=“excellent” or
$\mathbf {P}$
=“excellent” or
![]() $\mathbf {P}$
=“universally catenary” [Reference Greco7]. We refer the reader to [Reference Kurano and Shimomoto15, Appendix] for more information.
$\mathbf {P}$
=“universally catenary” [Reference Greco7]. We refer the reader to [Reference Kurano and Shimomoto15, Appendix] for more information.
One main objective of this article is to show that the property of admitting a dualizing complex satisfies the lifting property, which, as fundamental as it may be, seems to be missing in the literature. For applications, especially Theorem 6.5, we consider the following generalization of dualizing complexes to infinite-dimensional rings.
Definition 1.2. Let A be a Noetherian ring. Let
![]() $K\in D(A)$
. We say K is a pseudo-dualizing complex if
$K\in D(A)$
. We say K is a pseudo-dualizing complex if
![]() $K\in D^b_{Coh}(A)$
and
$K\in D^b_{Coh}(A)$
and
![]() $K_{\mathfrak {p}}$
is a dualizing complex for
$K_{\mathfrak {p}}$
is a dualizing complex for
![]() $A_{\mathfrak {p}}$
for all
$A_{\mathfrak {p}}$
for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
.
$\mathfrak {p}\in \operatorname {Spec}(A)$
.
We now state our main result (Theorem 5.1) on lifting. Note that applying to the case A local and I maximal, we recover the existence of dualizing complexes for Noetherian complete local rings. Therefore, this fact now admits a proof that does not use the Cohen structure theorem.
Theorem 1.3. Let A be a Noetherian ring, I an ideal of A. Assume that A is I-adically complete. If
![]() $A/I$
admits a pseudo-dualizing (resp. dualizing) complex
$A/I$
admits a pseudo-dualizing (resp. dualizing) complex
![]() $K_1$
, then A admits a pseudo-dualizing (resp. dualizing) complex K such that
$K_1$
, then A admits a pseudo-dualizing (resp. dualizing) complex K such that
![]() $R\operatorname {Hom}_{A}(A/I,K)\cong K_1$
.
$R\operatorname {Hom}_{A}(A/I,K)\cong K_1$
.
This result implies, quite formally, certain openness results (Theorem 6.2 and Corollary 6.3). In turn, we characterize when a Noetherian scheme of dimension 1 admits a dualizing complex (Corollary 7.6) and obtain that a quasi-excellent ring admits a pseudo-dualizing complex étale-locally (Theorem 6.5), via a known result of Hinich [Reference Hinich11] that an excellent Henselian local ring admits a dualizing complex. We point out to the reader that the results in Section 6 are new even for finite-dimensional rings to the best of our knowledge, except where noted.
Another main objective of this article is to illustrate that Definition 1.2 is, hopefully, a robust generalization of the classical concept of dualizing complexes. We show that pseudo-dualizing complexes are preserved by upper shriek (Corollary 4.5), induce a dualizing functor on
![]() $D^b_{Coh}$
(Corollary 4.9), and are unique up to twist (Corollary 4.11). The author believes it should be possible to develop the coherent duality theory for infinite-dimensional schemes using pseudo-dualizing complexes in place of dualizing complexes. Moreover, Sharp’s conjecture is true in this generality by the same proof, see Theorem 4.12. One can also expect that the concept of fundamental dualizing complexes [Reference Hall9] and related results can be extended to this generality.
$D^b_{Coh}$
(Corollary 4.9), and are unique up to twist (Corollary 4.11). The author believes it should be possible to develop the coherent duality theory for infinite-dimensional schemes using pseudo-dualizing complexes in place of dualizing complexes. Moreover, Sharp’s conjecture is true in this generality by the same proof, see Theorem 4.12. One can also expect that the concept of fundamental dualizing complexes [Reference Hall9] and related results can be extended to this generality.
To make our article accessible to a broader audience, we do not use
![]() $\mathbf {E}_\infty $
- or animated rings and the derived
$\mathbf {E}_\infty $
- or animated rings and the derived
![]() $\infty $
-category, although they helped a lot in the thought process. The author hopes that many results in this article can be generalized to truncated animated rings and dgas. We also produce an alternative proof of Hinich’s result, avoiding the use of dgas in the original proof. In exchange, we use ultrapowers of a local ring. We show a flatness result (Theorem 3.2) that may be of independent interest. It is a strengthening of [Reference Lyu17, Lemma 3.5]. We will not use Hinich’s result except for Theorem 6.5.
$\infty $
-category, although they helped a lot in the thought process. The author hopes that many results in this article can be generalized to truncated animated rings and dgas. We also produce an alternative proof of Hinich’s result, avoiding the use of dgas in the original proof. In exchange, we use ultrapowers of a local ring. We show a flatness result (Theorem 3.2) that may be of independent interest. It is a strengthening of [Reference Lyu17, Lemma 3.5]. We will not use Hinich’s result except for Theorem 6.5.
Our article is structured as follows. Section 2 is a short preparation. In Section 3, we give an alternative proof of Hinich’s result. In Section 4, we introduce pseudo-dualizing complexes and show several desirable properties. In Section 5, we prove our main result on formal lifting. In Sections 6 and 7, we discuss consequences. Finally, in Section 8, we make some remarks on quotient of Cohen–Macaulay rings that do not rely on the material on pseudo-dualizing complexes.
We thank Rankeya Datta, Longke Tang, and Kevin Tucker for helpful discussions. We thank Karl Schwede and Kevin Tucker for bringing the lifting problem of dualizing complexes to the author’s attention.
We use the following facts about dualizing complexes for local rings without explicit reference. They all follow from [25, Tag 0A7U], for
![]() $M=A$
.
$M=A$
.
Fact 1.4. Let A be a Noetherian local ring, K a dualizing complex for A. Then
![]() $\dim A-\operatorname {depth} A=\max \{b-a\mid a\leq b, H^a(K)\neq 0, H^b(K)\neq 0\}$
. If
$\dim A-\operatorname {depth} A=\max \{b-a\mid a\leq b, H^a(K)\neq 0, H^b(K)\neq 0\}$
. If
![]() $a\in \mathbf {Z}$
is such that
$a\in \mathbf {Z}$
is such that
![]() $\dim \operatorname {Supp}(H^a(K))=\dim A$
, then
$\dim \operatorname {Supp}(H^a(K))=\dim A$
, then
![]() $K\in D^{\geq a}(A)$
. K is normalized if and only if the minimal a so that
$K\in D^{\geq a}(A)$
. K is normalized if and only if the minimal a so that
![]() $H^a(K)\neq 0$
is
$H^a(K)\neq 0$
is
![]() $-\dim A$
.
$-\dim A$
.
2 Bounded pseudo-coherent complexes
Lemma 2.1. Let A be a Noetherian ring. Let
![]() $K,M\in D^b_{Coh}(A)$
. Let S be a multiplicative subset of A. Assume
$K,M\in D^b_{Coh}(A)$
. Let S be a multiplicative subset of A. Assume
![]() $S^{-1}K\cong S^{-1}M$
. Then for some
$S^{-1}K\cong S^{-1}M$
. Then for some
![]() $f\in S$
,
$f\in S$
,
![]() $K_f\cong M_f$
.
$K_f\cong M_f$
.
Proof. For any
![]() $X,Y\in D^b_{Coh}(A)$
, we have
$X,Y\in D^b_{Coh}(A)$
, we have
by [25, Tag 0A6A]. Thus, we can spread out a quasi-isomorphism and its inverse and the results are inverse quasi-isomophisms.
Lemma 2.2. Let
![]() $(A_i)_i$
be a direct system of rings,
$(A_i)_i$
be a direct system of rings,
![]() $A=\operatorname {colim}_i A_i$
. Assume that
$A=\operatorname {colim}_i A_i$
. Assume that
![]() $A_i\to A$
is flat for all i. Let
$A_i\to A$
is flat for all i. Let
![]() $K\in D^b(A)$
. Assume K is pseudo-coherent. Then
$K\in D^b(A)$
. Assume K is pseudo-coherent. Then
![]() $K\cong K_i^{\bullet }\otimes _{A_i}^L A$
for some i and some finite complex
$K\cong K_i^{\bullet }\otimes _{A_i}^L A$
for some i and some finite complex
![]() $K_i^{\bullet }$
of finitely presented
$K_i^{\bullet }$
of finitely presented
![]() $A_i$
-modules.
$A_i$
-modules.
If
![]() $a\leq b\in \mathbf {Z}$
are given such that
$a\leq b\in \mathbf {Z}$
are given such that
![]() $K\in D^{[a,b]}(A)$
, we can choose
$K\in D^{[a,b]}(A)$
, we can choose
![]() $K_i^{\bullet }$
so that
$K_i^{\bullet }$
so that
![]() $K_i^m=0$
for all
$K_i^m=0$
for all
![]() $m\not \in [a,b]$
and
$m\not \in [a,b]$
and
![]() $K_i^m$
free for all
$K_i^m$
free for all
![]() $a<m\leq b$
.
$a<m\leq b$
.
Proof.
K is represented by a bounded above complex
![]() $F^{\bullet }$
of finite free A-modules such that
$F^{\bullet }$
of finite free A-modules such that
![]() $F^m=0$
for all
$F^m=0$
for all
![]() $m>b$
. Let
$m>b$
. Let
![]() $K^{\bullet }$
be the complex of A-modules with
$K^{\bullet }$
be the complex of A-modules with
![]() $K^m=F^m\ (m> a), K^{a}=\operatorname {coker}(F^{a-1}\to F^a), K^m=0\ (m<a)$
, that is,
$K^m=F^m\ (m> a), K^{a}=\operatorname {coker}(F^{a-1}\to F^a), K^m=0\ (m<a)$
, that is,
![]() $K^{\bullet }$
is the canonical truncation
$K^{\bullet }$
is the canonical truncation
![]() $\tau _{\geq a}F^{\bullet }$
. Then
$\tau _{\geq a}F^{\bullet }$
. Then
![]() $K^{\bullet }$
also represents K, and
$K^{\bullet }$
also represents K, and
![]() $K^{\bullet }$
is a finite complex of finitely presented A-modules such that
$K^{\bullet }$
is a finite complex of finitely presented A-modules such that
![]() $K^m=0$
for all
$K^m=0$
for all
![]() $m\not \in [a,b]$
and
$m\not \in [a,b]$
and
![]() $K^m$
free for all
$K^m$
free for all
![]() $a<m\leq b$
. By [25, Tag 05N7], there exists an index i and a complex of finitely presented
$a<m\leq b$
. By [25, Tag 05N7], there exists an index i and a complex of finitely presented
![]() $A_i$
-modules
$A_i$
-modules
![]() $K_i^{\bullet }$
such that
$K_i^{\bullet }$
such that
![]() $K_i^m=0$
for all
$K_i^m=0$
for all
![]() $m\not \in [a,b]$
and
$m\not \in [a,b]$
and
![]() $K_i^m$
free for all
$K_i^m$
free for all
![]() $a<m\leq b$
, and that
$a<m\leq b$
, and that
![]() $K_i^{\bullet }\otimes _{A_i}A$
is isomorphic to
$K_i^{\bullet }\otimes _{A_i}A$
is isomorphic to
![]() $K^{\bullet }$
as cochain complexes. Since
$K^{\bullet }$
as cochain complexes. Since
![]() $A_i\to A$
is flat,
$A_i\to A$
is flat,
![]() $K\cong K_i^{\bullet }\otimes _{A_i}^L A$
.
$K\cong K_i^{\bullet }\otimes _{A_i}^L A$
.
3 Dualizing complexes for Henselian local rings
In this section, we prove a generalization of the main result of [Reference Hinich11], Theorem 3.5. We will only use the original result of [Reference Hinich11] for the application, Theorem 6.5.
For ultraproducts of rings, first-order statements, and Łoś’s Theorem, see [Reference Schoutens23, Chapter 2].
Lemma 3.1. Let A be a Noetherian local ring or an ultraproduct of Noetherian local rings,
![]() $f\in A$
a noninvertible nonzerodivisor. Let
$f\in A$
a noninvertible nonzerodivisor. Let
![]() $(E^{\bullet },d^{\bullet })$
be a cochain complex of A-modules. If
$(E^{\bullet },d^{\bullet })$
be a cochain complex of A-modules. If
![]() $E^{\bullet }/fE^{\bullet }$
is exact at some degree m and
$E^{\bullet }/fE^{\bullet }$
is exact at some degree m and
![]() $E^{m-1},E^m,E^{m+1}$
are finite free, then
$E^{m-1},E^m,E^{m+1}$
are finite free, then
![]() $E^{\bullet }$
is exact at degree m.
$E^{\bullet }$
is exact at degree m.
Proof. Choose a basis of
![]() $E^{m-1},E^m,E^{m+1}$
, so
$E^{m-1},E^m,E^{m+1}$
, so
![]() $d^{m-1}$
and
$d^{m-1}$
and
![]() $d^m$
are represented by matrices with coefficients in A. The statement of the lemma is a first-order statement of the coefficients and f, so it suffices to show the lemma for a Noetherian local A.
$d^m$
are represented by matrices with coefficients in A. The statement of the lemma is a first-order statement of the coefficients and f, so it suffices to show the lemma for a Noetherian local A.
The condition
![]() $E^{\bullet }/fE^{\bullet }$
is exact at degree m implies
$E^{\bullet }/fE^{\bullet }$
is exact at degree m implies
![]() $\ker (d^m)=\operatorname {im}(d^{m-1})+(fE^m\cap \ker (d^m))$
. Since f is a nonzerodivisor on
$\ker (d^m)=\operatorname {im}(d^{m-1})+(fE^m\cap \ker (d^m))$
. Since f is a nonzerodivisor on
![]() $E^{m+1}$
,
$E^{m+1}$
,
![]() $fE^m\cap \ker (d^m)=f\ker (d^m)$
. Thus,
$fE^m\cap \ker (d^m)=f\ker (d^m)$
. Thus,
![]() $\ker (d^m)=\operatorname {im}(d^{m-1})+f \ker (d^m)$
. By Nakayama’s Lemma,
$\ker (d^m)=\operatorname {im}(d^{m-1})+f \ker (d^m)$
. By Nakayama’s Lemma,
![]() $\ker (d^m)=\operatorname {im}(d^{m-1})$
.
$\ker (d^m)=\operatorname {im}(d^{m-1})$
.
Theorem 3.2. Let
![]() $(A,\mathfrak {m},k)$
be a Noetherian local ring,
$(A,\mathfrak {m},k)$
be a Noetherian local ring,
![]() $(B,\mathfrak {n},l)$
a Noetherian local flat A-algebra with
$(B,\mathfrak {n},l)$
a Noetherian local flat A-algebra with
![]() $\mathfrak {n}=\mathfrak {m} B$
. Let
$\mathfrak {n}=\mathfrak {m} B$
. Let
![]() $A_\natural $
be an ultrapower of A. Then any A-algebra map
$A_\natural $
be an ultrapower of A. Then any A-algebra map
![]() $B\to A_\natural $
, if exists, is faithfully flat.
$B\to A_\natural $
, if exists, is faithfully flat.
Proof. Since
![]() $A_\natural /\mathfrak {m} A_\natural \neq 0$
, it suffices to show
$A_\natural /\mathfrak {m} A_\natural \neq 0$
, it suffices to show
![]() $B\to A_\natural $
is flat.
$B\to A_\natural $
is flat.
We know
![]() $A\to A_\natural $
is flat [Reference Schoutens23, Corollary 3.3.3]. By [25, Tag 051C], we may base change to the reduction of A and assume A reduced. If
$A\to A_\natural $
is flat [Reference Schoutens23, Corollary 3.3.3]. By [25, Tag 051C], we may base change to the reduction of A and assume A reduced. If
![]() ${\dim A=0}$
, then
${\dim A=0}$
, then
![]() $A=k$
, so
$A=k$
, so
![]() $B=l$
is a field. Thus, we may assume
$B=l$
is a field. Thus, we may assume
![]() $\dim A>0,$
so
$\dim A>0,$
so
![]() $\operatorname {depth} A>0.$
$\operatorname {depth} A>0.$
We need to show
![]() $N\otimes _B^L A_\natural $
is concentrated in degree
$N\otimes _B^L A_\natural $
is concentrated in degree
![]() $0$
for all finite B-modules N. If
$0$
for all finite B-modules N. If
![]() $N=l$
, then since
$N=l$
, then since
![]() $\mathfrak {n}=\mathfrak {m} B$
,
$\mathfrak {n}=\mathfrak {m} B$
,
![]() $N\otimes _B^L A_\natural =k\otimes _A^L A_\natural $
is concentrated in degree
$N\otimes _B^L A_\natural =k\otimes _A^L A_\natural $
is concentrated in degree
![]() $0$
as
$0$
as
![]() $A\to A_\natural $
is flat. Thus,
$A\to A_\natural $
is flat. Thus,
![]() $N\otimes _B^L A_\natural $
is concentrated in degree
$N\otimes _B^L A_\natural $
is concentrated in degree
![]() $0$
for all N of finite length.
$0$
for all N of finite length.
For a general N, we may assume, by Noetherian induction, that
![]() $\overline {N}\otimes _B^L A_\natural $
is concentrated in degree
$\overline {N}\otimes _B^L A_\natural $
is concentrated in degree
![]() $0$
for all proper quotients
$0$
for all proper quotients
![]() $\overline {N}$
of N. Since
$\overline {N}$
of N. Since
![]() $N[\mathfrak {n}^\infty ]$
is of finite length, we may thus assume
$N[\mathfrak {n}^\infty ]$
is of finite length, we may thus assume
![]() $N[\mathfrak {n}^\infty ]=0$
, i.e.,
$N[\mathfrak {n}^\infty ]=0$
, i.e.,
![]() $\operatorname {depth} N>0$
.
$\operatorname {depth} N>0$
.
Since
![]() $\operatorname {depth} A>0$
and since
$\operatorname {depth} A>0$
and since
![]() $\mathfrak {m} B=\mathfrak {n}$
, there exists an
$\mathfrak {m} B=\mathfrak {n}$
, there exists an
![]() $f\in \mathfrak {m}$
that is both a nonzerodivisor in A (thus a noninvertible nonzerodivisor in both B and
$f\in \mathfrak {m}$
that is both a nonzerodivisor in A (thus a noninvertible nonzerodivisor in both B and
![]() $A_\natural $
) and a nonzerodivisor in N. Thus,
$A_\natural $
) and a nonzerodivisor in N. Thus,
![]() $N\otimes _B^L A_\natural /fA_\natural \cong N/fN \otimes _B^L A_\natural $
is concentrated in degree
$N\otimes _B^L A_\natural /fA_\natural \cong N/fN \otimes _B^L A_\natural $
is concentrated in degree
![]() $0$
. Since N and thus
$0$
. Since N and thus
![]() $N\otimes _B^L A_\natural $
can be represented by a complex of finite free modules, Lemma 3.1 implies that
$N\otimes _B^L A_\natural $
can be represented by a complex of finite free modules, Lemma 3.1 implies that
![]() $N\otimes _B^L A_\natural $
is concentrated in degree
$N\otimes _B^L A_\natural $
is concentrated in degree
![]() $0$
.
$0$
.
Lemma 3.3. Let
![]() $(A,\mathfrak {m},k)$
be a Noetherian local ring,
$(A,\mathfrak {m},k)$
be a Noetherian local ring,
![]() $d=\dim A$
. Let
$d=\dim A$
. Let
![]() $b\in \mathbf {Z}$
and let
$b\in \mathbf {Z}$
and let
![]() $M\in D^{\leq b}_{Coh}(A)$
. If
$M\in D^{\leq b}_{Coh}(A)$
. If
![]() $\operatorname {Ext}^m_{A}(k,M)=0$
for all
$\operatorname {Ext}^m_{A}(k,M)=0$
for all
![]() $b+1\leq m\leq b+d+1$
, then
$b+1\leq m\leq b+d+1$
, then
![]() $\operatorname {Ext}^m_{A}(N,M)=0$
for all
$\operatorname {Ext}^m_{A}(N,M)=0$
for all
![]() $m>b$
and all finite A-modules N.
$m>b$
and all finite A-modules N.
Proof. We show by induction on
![]() $h=\dim \operatorname {Supp} N$
that
$h=\dim \operatorname {Supp} N$
that
![]() $\operatorname {Ext}^m_{A}(N,M)=0$
for all
$\operatorname {Ext}^m_{A}(N,M)=0$
for all
![]() $b+1\leq m\leq b+d+1-h$
, for all finite A-modules N. This implies the result, since then
$b+1\leq m\leq b+d+1-h$
, for all finite A-modules N. This implies the result, since then
![]() $\operatorname {Ext}^{b+1}_{A}(N,M)=0$
for all finite A-modules N, so dimension shifting and the fact
$\operatorname {Ext}^{b+1}_{A}(N,M)=0$
for all finite A-modules N, so dimension shifting and the fact
![]() $M\in D^{\leq b}(A)$
shows
$M\in D^{\leq b}(A)$
shows
![]() $\operatorname {Ext}^{m}_{A}(N,M)=0$
for all finite A-modules N and all
$\operatorname {Ext}^{m}_{A}(N,M)=0$
for all finite A-modules N and all
![]() $m>b$
.
$m>b$
.
If
![]() $h=0$
, then N has finite length, thus is a successive extension of k and the vanishing holds by the assumption. Assume
$h=0$
, then N has finite length, thus is a successive extension of k and the vanishing holds by the assumption. Assume
![]() $h>0$
, so there exists
$h>0$
, so there exists
![]() $f\in \mathfrak {m}$
such that
$f\in \mathfrak {m}$
such that
![]() $\dim \left ( V(fA)\cap \operatorname {Supp} N\right )<h$
. Let
$\dim \left ( V(fA)\cap \operatorname {Supp} N\right )<h$
. Let
![]() $C=\operatorname {Cone}(N\xrightarrow {\times f}N)$
, so we have a distinguished triangle
$C=\operatorname {Cone}(N\xrightarrow {\times f}N)$
, so we have a distinguished triangle
![]() $N\xrightarrow {\times f}N\to C\to +1$
. We note that
$N\xrightarrow {\times f}N\to C\to +1$
. We note that
![]() $C\in D^{[-1,0]}_{Coh}(A)$
and that the dimension of the support of the cohomology modules of C is less than h. Thus, the induction hypothesis tells us
$C\in D^{[-1,0]}_{Coh}(A)$
and that the dimension of the support of the cohomology modules of C is less than h. Thus, the induction hypothesis tells us
![]() $\operatorname {Ext}^m_{A}(C,M)=0$
for all
$\operatorname {Ext}^m_{A}(C,M)=0$
for all
![]() $b+2\leq m\leq b+d+2-h$
. The distinguished triangle above and Nakayama’s Lemma tells us
$b+2\leq m\leq b+d+2-h$
. The distinguished triangle above and Nakayama’s Lemma tells us
![]() $\operatorname {Ext}^m_{A}(N,M)=0$
for all
$\operatorname {Ext}^m_{A}(N,M)=0$
for all
![]() $b+1\leq m\leq b+d+1-h$
, as desired.
$b+1\leq m\leq b+d+1-h$
, as desired.
Corollary 3.4. Let
![]() $(A,\mathfrak {m},k)$
be a Noetherian local ring of dimension d, and let
$(A,\mathfrak {m},k)$
be a Noetherian local ring of dimension d, and let
![]() $a\in \mathbf {Z}$
. Let
$a\in \mathbf {Z}$
. Let
![]() $M\in D^{[a,0]}_{Coh}(A)$
. Assume that
$M\in D^{[a,0]}_{Coh}(A)$
. Assume that
 $$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A}(k,M)&\cong k.\\ \tau_{\geq a}\tau_{\leq -a}R\operatorname{Hom}_{A}(M,M)&=A. \end{align*} $$
$$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A}(k,M)&\cong k.\\ \tau_{\geq a}\tau_{\leq -a}R\operatorname{Hom}_{A}(M,M)&=A. \end{align*} $$
Then M is a normalized dualizing complex.
Proof. By Lemma 3.3,
![]() $\operatorname {Ext}^m_A(N,M)=0$
for all finite A-modules N and all
$\operatorname {Ext}^m_A(N,M)=0$
for all finite A-modules N and all
![]() $m>0$
. Thus, M has injective amplitude
$m>0$
. Thus, M has injective amplitude
![]() $[a,0]$
and
$[a,0]$
and
![]() $R\operatorname {Hom}_{A}(k,M)\cong k$
. Since
$R\operatorname {Hom}_{A}(k,M)\cong k$
. Since
![]() $M\in D^{[a,0]}(A)$
, we see
$M\in D^{[a,0]}(A)$
, we see
![]() $R\operatorname {Hom}_{A}(M,M)\in D^{[a,-a]}(A)$
. Thus,
$R\operatorname {Hom}_{A}(M,M)\in D^{[a,-a]}(A)$
. Thus,
![]() $R\operatorname {Hom}_{A}(M,M)=A$
, so M is a normalized dualizing complex.
$R\operatorname {Hom}_{A}(M,M)=A$
, so M is a normalized dualizing complex.
Theorem 3.5. Let
![]() $(A,I)$
be a Henselian pair where
$(A,I)$
be a Henselian pair where
![]() $(A,\mathfrak {m},k)$
is a Noetherian local ring. Assume that
$(A,\mathfrak {m},k)$
is a Noetherian local ring. Assume that
-
(i) The I-adic completion map
 $A\to B:=\lim _n A/I^n$
is regular.
$A\to B:=\lim _n A/I^n$
is regular. -
(ii) B admits a dualizing complex.
Then A admits a dualizing complex.
Note that (i) is always true for quasi-excellent A, see [25, Tag 0AH2].
Proof. By Popescu’s theorem [25, Tag 07GC], B is the colimit of a direct system of smooth A-algebras
![]() $A_i$
. The composition
$A_i$
. The composition
![]() $A_i\to B\to B/IB\cong A/I$
gives an A-algebra map
$A_i\to B\to B/IB\cong A/I$
gives an A-algebra map
![]() $A_i\to A/I$
, thus
$A_i\to A/I$
, thus
![]() $A_i$
admits a section
$A_i$
admits a section
![]() $A_i\to A$
since
$A_i\to A$
since
![]() $(A,I)$
is Henselian, see [25, Tag 07M7]. Thus [Reference Schoutens23, Theorem 7.1.1] applies (see also [Reference Lyu17, Lemma 3.4]), so there exists an A-algebra map
$(A,I)$
is Henselian, see [25, Tag 07M7]. Thus [Reference Schoutens23, Theorem 7.1.1] applies (see also [Reference Lyu17, Lemma 3.4]), so there exists an A-algebra map
![]() $B\to A_\natural $
where
$B\to A_\natural $
where
![]() $A_\natural =A^X/\mathcal {U}=S_{\mathcal {U}}^{-1}A^X$
is an ultrapower of A. Here X is a set,
$A_\natural =A^X/\mathcal {U}=S_{\mathcal {U}}^{-1}A^X$
is an ultrapower of A. Here X is a set,
![]() $\mathcal {U}$
is an ultrafilter on X, and
$\mathcal {U}$
is an ultrafilter on X, and
![]() $S_{\mathcal {U}}=\{e_U\mid U\in \mathcal {U}\}$
, where
$S_{\mathcal {U}}=\{e_U\mid U\in \mathcal {U}\}$
, where
![]() $e_U$
is defined by
$e_U$
is defined by
![]() $(e_U)_x=1$
when
$(e_U)_x=1$
when
![]() $x\in U$
and
$x\in U$
and
![]() $(e_U)_x=0$
when
$(e_U)_x=0$
when
![]() $x\not \in U$
. This map is flat by Theorem 3.2.
$x\not \in U$
. This map is flat by Theorem 3.2.
Let
![]() $K\in D^b_{Coh}(B)$
be a normalized dualizing complex. Then
$K\in D^b_{Coh}(B)$
be a normalized dualizing complex. Then
![]() $F:=K\otimes _B^L A_\natural \in D(A_\natural )$
is pseudo-coherent and bounded. Writing
$F:=K\otimes _B^L A_\natural \in D(A_\natural )$
is pseudo-coherent and bounded. Writing
![]() $k_\natural =k\otimes _A^L A_\natural =k\otimes _B^L A_\natural $
, we have
$k_\natural =k\otimes _A^L A_\natural =k\otimes _B^L A_\natural $
, we have
 $$ \begin{align*} R\operatorname{Hom}_{A_\natural}(k_\natural,F)&=R\operatorname{Hom}_{B}(k,K)\otimes_B^L A_\natural\cong k_\natural,\\ R\operatorname{Hom}_{A_\natural}(F,F)&=R\operatorname{Hom}_{B}(K,K)\otimes_B^L A_\natural= A_\natural, \end{align*} $$
$$ \begin{align*} R\operatorname{Hom}_{A_\natural}(k_\natural,F)&=R\operatorname{Hom}_{B}(k,K)\otimes_B^L A_\natural\cong k_\natural,\\ R\operatorname{Hom}_{A_\natural}(F,F)&=R\operatorname{Hom}_{B}(K,K)\otimes_B^L A_\natural= A_\natural, \end{align*} $$
by [25, Tag 0A6A] and by the fact K is a normalized dualizing complex.
Let
![]() $d=\dim A$
. Then
$d=\dim A$
. Then
![]() $K\in D^{[-d, 0]}(B)$
and thus
$K\in D^{[-d, 0]}(B)$
and thus
![]() $F\in D^{[-d, 0]}(A_\natural )$
. By Lemma 2.2, there exists an
$F\in D^{[-d, 0]}(A_\natural )$
. By Lemma 2.2, there exists an
![]() $e\in S_{\mathcal {U}}$
and an
$e\in S_{\mathcal {U}}$
and an
![]() $M\in D((A^X)_e)$
represented by a complex
$M\in D((A^X)_e)$
represented by a complex
![]() $M^{\bullet }$
of finitely presented
$M^{\bullet }$
of finitely presented
![]() $(A^X)_e$
-modules such that
$(A^X)_e$
-modules such that
![]() $M\otimes ^L_{(A^X)_e}A_\natural \cong F$
, that
$M\otimes ^L_{(A^X)_e}A_\natural \cong F$
, that
![]() $M^m=0$
for all
$M^m=0$
for all
![]() $m>0$
and
$m>0$
and
![]() $m<-d$
, and that
$m<-d$
, and that
![]() $M^m$
is free for all
$M^m$
is free for all
![]() $-d<m\leq 0$
. Note that if
$-d<m\leq 0$
. Note that if
![]() $e=e_U$
, then
$e=e_U$
, then
![]() $(A^X)_e=A^U$
, thus after replacing X by a subset in
$(A^X)_e=A^U$
, thus after replacing X by a subset in
![]() $\mathcal {U}$
we may assume
$\mathcal {U}$
we may assume
![]() $e=1$
.
$e=1$
.
We note that another application of Lemma 2.2 with
![]() $a=-2d$
shows that, after replacing X by a subset, M is also represented by a complex of free A-modules
$a=-2d$
shows that, after replacing X by a subset, M is also represented by a complex of free A-modules
![]() $P^{\bullet }$
such that
$P^{\bullet }$
such that
![]() $P^m=0$
for all
$P^m=0$
for all
![]() $m>0$
and that
$m>0$
and that
![]() $P^m$
is finite for all
$P^m$
is finite for all
![]() $m\geq -2d-1$
. Thus,
$m\geq -2d-1$
. Thus,
![]() $R\operatorname {Hom}_{A^X}(M,M)$
is represented by the Hom complex
$R\operatorname {Hom}_{A^X}(M,M)$
is represented by the Hom complex
![]() $E^{\bullet }:=\operatorname {Hom}^{\bullet }_{A^X}(P^{\bullet },M^{\bullet })$
, and
$E^{\bullet }:=\operatorname {Hom}^{\bullet }_{A^X}(P^{\bullet },M^{\bullet })$
, and
![]() $E^m$
is finitely presented for all
$E^m$
is finitely presented for all
![]() $m\leq d+1$
. Also note that
$m\leq d+1$
. Also note that
![]() $R\operatorname {Hom}_{A^X}(k^X,M)$
is represented by a complex of finitely presented modules in degrees
$R\operatorname {Hom}_{A^X}(k^X,M)$
is represented by a complex of finitely presented modules in degrees
![]() $\geq -d$
, since
$\geq -d$
, since
![]() $k^X=A^X\otimes ^L_A k$
is represented by a complex of finite free modules in degrees
$k^X=A^X\otimes ^L_A k$
is represented by a complex of finite free modules in degrees
![]() $\leq 0$
.
$\leq 0$
.
Let
![]() $T^{-1}\to T^0\to T$
be a three-term complex of finitely presented
$T^{-1}\to T^0\to T$
be a three-term complex of finitely presented
![]() $A^X$
-modules. Fix presentations
$A^X$
-modules. Fix presentations
![]() $P^{i,-1}\to P^{i,0}\to T^{i}\to 0\ (i=-1,0,1)$
, where
$P^{i,-1}\to P^{i,0}\to T^{i}\to 0\ (i=-1,0,1)$
, where
![]() $P^{i,j}$
are finite free, and maps
$P^{i,j}$
are finite free, and maps
![]() $P^{-1,0}\to P^{0,0}\to P^{1,0}$
lifting
$P^{-1,0}\to P^{0,0}\to P^{1,0}$
lifting
![]() $T^{-1}\to T^0\to T^1$
. We do not require the composition
$T^{-1}\to T^0\to T^1$
. We do not require the composition
![]() $P^{-1,0}\to P^{1,0}$
to be zero. Fix bases of
$P^{-1,0}\to P^{1,0}$
to be zero. Fix bases of
![]() $P^{i,j}$
, so the maps between
$P^{i,j}$
, so the maps between
![]() $P^{i,j}$
are represented by matrices. The statement that the cohomology
$P^{i,j}$
are represented by matrices. The statement that the cohomology
![]() $\ker (T^0\to T^1)/\operatorname {im}(T^{-1}\to T^0)$
is
$\ker (T^0\to T^1)/\operatorname {im}(T^{-1}\to T^0)$
is
![]() $0$
(resp.
$0$
(resp.
![]() $A^X,k^X$
) is a first-order statement of the coefficients of the matrices. This observation and the observation on Hom complexes above tells us that after replacing X by a subset in
$A^X,k^X$
) is a first-order statement of the coefficients of the matrices. This observation and the observation on Hom complexes above tells us that after replacing X by a subset in
![]() $\mathcal {U}$
, we have
$\mathcal {U}$
, we have
 $$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A^X}(k^X,M)&\cong k^X,\\ \tau_{\geq -d}\tau_{\leq d}R\operatorname{Hom}_{A^X}(M,M)&=A^X. \end{align*} $$
$$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A^X}(k^X,M)&\cong k^X,\\ \tau_{\geq -d}\tau_{\leq d}R\operatorname{Hom}_{A^X}(M,M)&=A^X. \end{align*} $$
Apply the projection
![]() $A^X\to A$
to some coordinate, we get an object
$A^X\to A$
to some coordinate, we get an object
![]() $M_1\in D^{[-d,0]}_{Coh}(A)$
such that
$M_1\in D^{[-d,0]}_{Coh}(A)$
such that
 $$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A}(k,M_1)&\cong k,\\ \tau_{\geq -d}\tau_{\leq d}R\operatorname{Hom}_{A}(M_1,M_1)&=A. \end{align*} $$
$$ \begin{align*} \tau_{\leq d+1}R\operatorname{Hom}_{A}(k,M_1)&\cong k,\\ \tau_{\geq -d}\tau_{\leq d}R\operatorname{Hom}_{A}(M_1,M_1)&=A. \end{align*} $$
Then
![]() $M_1$
is a dualizing complex for A by Corollary 3.4.
$M_1$
is a dualizing complex for A by Corollary 3.4.
An elementary étale-local ring map is a local map
![]() $(R,\mathfrak {m},k)\to (S,\mathfrak {n},l)$
of local rings such that S is the localization of an étale R-algebra at a prime ideal and that
$(R,\mathfrak {m},k)\to (S,\mathfrak {n},l)$
of local rings such that S is the localization of an étale R-algebra at a prime ideal and that
![]() $l=k$
.
$l=k$
.
Corollary 3.6. Let A be a Noethrian local G-ring. Then there exists an elementary étale-local ring map
![]() $A\to A'$
such that
$A\to A'$
such that
![]() $A'$
admits a dualizing complex.
$A'$
admits a dualizing complex.
Proof. Let
![]() $A^h$
be the Henselization of A, so
$A^h$
be the Henselization of A, so
![]() $A^h$
is a Henselian G-ring [25, Tag 07QR]. Thus,
$A^h$
is a Henselian G-ring [25, Tag 07QR]. Thus,
![]() $A^h$
admits a dualizing complex
$A^h$
admits a dualizing complex
![]() ${K\in D(A^h)}$
by Theorem 3.5 (and [25, Tag 0BFR] or our Theorem 1.3). Since
${K\in D(A^h)}$
by Theorem 3.5 (and [25, Tag 0BFR] or our Theorem 1.3). Since
![]() $A\to A^h$
is the filtered colimit of elementary étale-local ring maps
$A\to A^h$
is the filtered colimit of elementary étale-local ring maps
![]() $A\to A'$
[25, Tag 04GN] and since each
$A\to A'$
[25, Tag 04GN] and since each
![]() $A'\to A^h$
is flat (cf. [25, Tag 08HS]), by Lemma 2.2 there exists an
$A'\to A^h$
is flat (cf. [25, Tag 08HS]), by Lemma 2.2 there exists an
![]() $A'$
and a
$A'$
and a
![]() $K'\in D^b_{Coh}(A')$
such that
$K'\in D^b_{Coh}(A')$
such that
![]() $K'\otimes ^L_{A'}A^h=K$
. Since K is a dualizing complex for
$K'\otimes ^L_{A'}A^h=K$
. Since K is a dualizing complex for
![]() $A^h$
, by flatness again we see
$A^h$
, by flatness again we see
![]() $K'$
is a dualizing complex for
$K'$
is a dualizing complex for
![]() $A'$
, see [25, Tag 0E4A].
$A'$
, see [25, Tag 0E4A].
4 Pseudo-dualizing complexes
Definition 4.1. Let A be a Noetherian ring. Let
![]() $K\in D(A)$
. We say K is a pseudo-dualizing complex if
$K\in D(A)$
. We say K is a pseudo-dualizing complex if
![]() $K\in D^b_{Coh}(A)$
and
$K\in D^b_{Coh}(A)$
and
![]() $K_{\mathfrak {p}}$
is a dualizing complex for
$K_{\mathfrak {p}}$
is a dualizing complex for
![]() $A_{\mathfrak {p}}$
for all
$A_{\mathfrak {p}}$
for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. Thus, A is Gorenstein if and only if
$\mathfrak {p}\in \operatorname {Spec}(A)$
. Thus, A is Gorenstein if and only if
![]() $A\in D(A)$
is a pseudo-dualizing complex.
$A\in D(A)$
is a pseudo-dualizing complex.
Let X be a Noetherian scheme.
![]() $K\in D(X)$
is a pseudo-dualizing complex if
$K\in D(X)$
is a pseudo-dualizing complex if
![]() $K\in D^b_{Coh}(X)$
and
$K\in D^b_{Coh}(X)$
and
![]() $K_x$
is a dualizing complex for
$K_x$
is a dualizing complex for
![]() $\mathcal {O}_{X,x}$
for all
$\mathcal {O}_{X,x}$
for all
![]() $x\in X$
.
$x\in X$
.
It is clear that
![]() $K\in D^b_{Coh}(A)$
is a pseudo-dualizing complex if and only if
$K\in D^b_{Coh}(A)$
is a pseudo-dualizing complex if and only if
![]() $K_{\mathfrak {m}}$
is a dualizing complex for
$K_{\mathfrak {m}}$
is a dualizing complex for
![]() $A_{\mathfrak {m}}$
for all maximal ideals
$A_{\mathfrak {m}}$
for all maximal ideals
![]() $\mathfrak {m}$
of A.
$\mathfrak {m}$
of A.
Remark 4.2. A pseudo-dualizing complex is a dualizing complex if and only if A (resp. X) is finite-dimensional. See [Reference Hartshorne10, Chapter V, Proposition 8.2].
The existence of a pseudo-dualizing complex implies being catenary, in fact implies the existence of a codimension function, see [Reference Hartshorne10, p. 287].
Lemma 4.3. Let A be a Noetherian ring. Assume that for every
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
,
$\mathfrak {p}\in \operatorname {Spec}(A)$
,
![]() $\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Let
$\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Let
![]() $K\in D(A)$
be such that
$K\in D(A)$
be such that
![]() $K_{\mathfrak {p}}$
is a dualizing complex for all
$K_{\mathfrak {p}}$
is a dualizing complex for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. Then K is bounded.
$\mathfrak {p}\in \operatorname {Spec}(A)$
. Then K is bounded.
Proof. For all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
, we have
$\mathfrak {p}\in \operatorname {Spec}(A)$
, we have
By [Reference Grothendieck8, Proposition 6.10.6], the function on the left-hand side is constructible on
![]() $\operatorname {Spec}(A)$
. Let N be the maximum of this function, and for each minimal prime
$\operatorname {Spec}(A)$
. Let N be the maximum of this function, and for each minimal prime
![]() $\mathfrak {q}$
of A let
$\mathfrak {q}$
of A let
![]() $c_{\mathfrak {q}}$
be the unique integer such that
$c_{\mathfrak {q}}$
be the unique integer such that
![]() $H^{c_{\mathfrak {q}}}(K_{\mathfrak {q}})\neq 0$
. Then it is clear that K is concentrated in degrees
$H^{c_{\mathfrak {q}}}(K_{\mathfrak {q}})\neq 0$
. Then it is clear that K is concentrated in degrees
![]() $[-N+\min _{\mathfrak {q}} c_{\mathfrak {q}},\max _{\mathfrak {q}} c_{\mathfrak {q}}+N]$
. (In fact,
$[-N+\min _{\mathfrak {q}} c_{\mathfrak {q}},\max _{\mathfrak {q}} c_{\mathfrak {q}}+N]$
. (In fact,
![]() $[\min _{\mathfrak {q}} c_{\mathfrak {q}},\max _{\mathfrak {q}} c_{\mathfrak {q}}+N]$
.)
$[\min _{\mathfrak {q}} c_{\mathfrak {q}},\max _{\mathfrak {q}} c_{\mathfrak {q}}+N]$
.)
Lemma 4.4. Let
![]() $f:A\to B$
be a finite map of Noetherian rings. Let
$f:A\to B$
be a finite map of Noetherian rings. Let
![]() $K\in D(A)$
be a pseudo-dualizing complex. Then
$K\in D(A)$
be a pseudo-dualizing complex. Then
![]() $L:=R\operatorname {Hom}_A(B,K)\in D(B)$
is a pseudo-dualizing complex.
$L:=R\operatorname {Hom}_A(B,K)\in D(B)$
is a pseudo-dualizing complex.
Proof. Since K is a pseudo-dualizing complex, we have, for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
,
$\mathfrak {p}\in \operatorname {Spec}(A)$
,
Since
![]() $K\in D^b_{Coh}(A)$
, the function on the right-hand side is constructible. Therefore, [Reference Grothendieck8, Proposition 6.10.6] shows that for every
$K\in D^b_{Coh}(A)$
, the function on the right-hand side is constructible. Therefore, [Reference Grothendieck8, Proposition 6.10.6] shows that for every
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
,
$\mathfrak {p}\in \operatorname {Spec}(A)$
,
![]() $\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Since B is finite over A the same is true for B. Since K is bounded,
$\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Since B is finite over A the same is true for B. Since K is bounded,
![]() $L\in D_{Coh}(B)$
. It is clear that
$L\in D_{Coh}(B)$
. It is clear that
![]() $L_{\mathfrak {q}}$
is a dualizing complex for
$L_{\mathfrak {q}}$
is a dualizing complex for
![]() $B_{\mathfrak {q}}$
for all
$B_{\mathfrak {q}}$
for all
![]() $\mathfrak {q}\in \operatorname {Spec}(B)$
. We conclude by Lemma 4.3.
$\mathfrak {q}\in \operatorname {Spec}(B)$
. We conclude by Lemma 4.3.
Lemma 4.4 has a number of consequences that tell us pseudo-dualizing complexes resemble various properties of dualizing complexes.
Corollary 4.5. Let
![]() $f:X\to Y$
be a morphism separated of finite type between Noetherian schemes. Then
$f:X\to Y$
be a morphism separated of finite type between Noetherian schemes. Then
![]() $f^!$
sends a pseudo-dualizing complex for Y to a pseudo-dualizing complex for X.
$f^!$
sends a pseudo-dualizing complex for Y to a pseudo-dualizing complex for X.
Proof. Recall that
![]() $f^!$
is well defined for all separated morphisms of finite type [25, Tag 0AA0], compatible with composition [25, Tag 0ATX], flat base change [25, Tag 0E9U], and open immersion [25, Tag 0AU0].
$f^!$
is well defined for all separated morphisms of finite type [25, Tag 0AA0], compatible with composition [25, Tag 0ATX], flat base change [25, Tag 0E9U], and open immersion [25, Tag 0AU0].
Let K be a pseudo-dualizing complex for Y. Since the result is true after base change to
![]() $\operatorname {Spec}(\mathcal {O}_{Y,y})$
for all
$\operatorname {Spec}(\mathcal {O}_{Y,y})$
for all
![]() $y\in Y$
[25, Tag 0AA3], we see
$y\in Y$
[25, Tag 0AA3], we see
![]() $(f^!K)_x$
is a dualizing complex for
$(f^!K)_x$
is a dualizing complex for
![]() $\mathcal {O}_{X,x}$
for all
$\mathcal {O}_{X,x}$
for all
![]() $x\in X$
. Thus it suffices to show
$x\in X$
. Thus it suffices to show
![]() $f^!K\in D^b_{Coh}(X)$
. We may assume X and Y affine by compatibility with open immersion. By compatibility with composition, it suffices to treat the cases
$f^!K\in D^b_{Coh}(X)$
. We may assume X and Y affine by compatibility with open immersion. By compatibility with composition, it suffices to treat the cases
![]() $X=\mathbf {A}^1_Y$
and f is finite (or even closed immersion). If
$X=\mathbf {A}^1_Y$
and f is finite (or even closed immersion). If
![]() $X=\mathbf {A}^1_Y$
the result is trivial, see [25, Tag 0AA1]. If f is finite, the result is true by [25, Tag 0AA2] and Lemma 4.4. Therefore, the result is true for any f.
$X=\mathbf {A}^1_Y$
the result is trivial, see [25, Tag 0AA1]. If f is finite, the result is true by [25, Tag 0AA2] and Lemma 4.4. Therefore, the result is true for any f.
Definition 4.6. Let A be a Noetherian ring. We say A is Gor-2 if
![]() $\operatorname {Spec}(A/\mathfrak {p})$
has a nonempty Gorenstein open subset for all
$\operatorname {Spec}(A/\mathfrak {p})$
has a nonempty Gorenstein open subset for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. This is equivalent to that the Gorenstein locus of any finite type A-algebra is open, see [Reference Greco and Marinari6, Proposition 1.7]. We recover this fact in Corollaries 4.8 and 6.3, and we will not use it.
$\mathfrak {p}\in \operatorname {Spec}(A)$
. This is equivalent to that the Gorenstein locus of any finite type A-algebra is open, see [Reference Greco and Marinari6, Proposition 1.7]. We recover this fact in Corollaries 4.8 and 6.3, and we will not use it.
A locally Noetherian scheme is Gor-2 if it can be covered by affine opens
![]() $\operatorname {Spec}(A)$
where A is Gor-2.
$\operatorname {Spec}(A)$
where A is Gor-2.
Corollary 4.7. Let A be a Noetherian ring that admits a pseudo-dualizing complex. Then every finite type A-algebra admits a pseudo-dualizing complex, and A is Gor-2 and universally catenary. In particular, a Gorenstein ring is Gor-2.
Proof. The “in particular” statement follows from the fact that A is a pseudo-dualizing complex for a Gorenstein A.
Every finite type A-algebra admits a pseudo-dualizing complex by Corollary 4.5, so A is universally catenary by Remark 4.2. To see A is Gor-2, we may assume by Lemma 4.4 that A is an integral domain, and we must show
![]() $A_f$
is Gorenstein for some nonzero f. This is clear: a pseudo-dualizing complex
$A_f$
is Gorenstein for some nonzero f. This is clear: a pseudo-dualizing complex
![]() $K\in D^b_{Coh}(A)$
is a shift of the fraction field at the generic point of A, thus for some
$K\in D^b_{Coh}(A)$
is a shift of the fraction field at the generic point of A, thus for some
![]() $f\neq 0$
,
$f\neq 0$
,
![]() $K_f$
is a shift of
$K_f$
is a shift of
![]() $A_f$
by Lemma 2.1.
$A_f$
by Lemma 2.1.
Corollary 4.8. Let A be a Noetherian ring that is Gor-2. Then every finite type A-algebra is Gor-2.
Proof. By definition, we may assume A Gorenstein, and we conclude by Corollary 4.7.
Corollary 4.9. Let A be a Noetherian ring,
![]() $K\in D(A)$
a pseudo-dualizing complex. Then the functor
$K\in D(A)$
a pseudo-dualizing complex. Then the functor
![]() $D_K(-)=R\operatorname {Hom}_A(-,K)$
maps
$D_K(-)=R\operatorname {Hom}_A(-,K)$
maps
![]() $D^b_{Coh}(A)$
into
$D^b_{Coh}(A)$
into
![]() $D^b_{Coh}(A)$
, and the canonical map
$D^b_{Coh}(A)$
, and the canonical map
![]() $\operatorname {id}\to D_K\circ D_K$
is an isomorphism of functors.
$\operatorname {id}\to D_K\circ D_K$
is an isomorphism of functors.
Proof. By Lemma 4.4,
![]() $D_K(A/\mathfrak {p})\in D^b_{Coh}(A)$
for all
$D_K(A/\mathfrak {p})\in D^b_{Coh}(A)$
for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. Thus
$\mathfrak {p}\in \operatorname {Spec}(A)$
. Thus
![]() $D_K$
maps
$D_K$
maps
![]() $D^b_{Coh}(A)$
into
$D^b_{Coh}(A)$
into
![]() $D^b_{Coh}(A)$
. The fact that
$D^b_{Coh}(A)$
. The fact that
![]() $\operatorname {id}\to D_K\circ D_K$
is an isomorphism can be checked locally by [25, Tag 0A6A], and the local case is well-known, cf. [25, Tag 0A7C].
$\operatorname {id}\to D_K\circ D_K$
is an isomorphism can be checked locally by [25, Tag 0A6A], and the local case is well-known, cf. [25, Tag 0A7C].
Remark 4.10. The functor
![]() $D_K(-)$
does not map
$D_K(-)$
does not map
![]() $D^+_{Coh}(A)$
into either
$D^+_{Coh}(A)$
into either
![]() $D^-(A)$
or
$D^-(A)$
or
![]() $D_{Coh}(A)$
when A is not finite-dimensional. To see this, for
$D_{Coh}(A)$
when A is not finite-dimensional. To see this, for
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
let
$\mathfrak {p}\in \operatorname {Spec}(A)$
let
![]() $a_{\mathfrak {p}}$
be the smallest integer with
$a_{\mathfrak {p}}$
be the smallest integer with
![]() $H^{a_{\mathfrak {p}}}(K_{\mathfrak {p}})\neq 0$
. Then
$H^{a_{\mathfrak {p}}}(K_{\mathfrak {p}})\neq 0$
. Then
![]() $\mathfrak {p}\mapsto a_{\mathfrak {p}}$
is a bounded function since K is bounded, and
$\mathfrak {p}\mapsto a_{\mathfrak {p}}$
is a bounded function since K is bounded, and
![]() $R\operatorname {Hom}_{A}(A/\mathfrak {m},K)\cong A/\mathfrak {m}[-a_{\mathfrak {m}}-\operatorname {ht}\mathfrak {m}]$
for all maximal ideals
$R\operatorname {Hom}_{A}(A/\mathfrak {m},K)\cong A/\mathfrak {m}[-a_{\mathfrak {m}}-\operatorname {ht}\mathfrak {m}]$
for all maximal ideals
![]() $\mathfrak {m}$
of A. Thus if we pick
$\mathfrak {m}$
of A. Thus if we pick
![]() $\mathfrak {m}_n$
so that
$\mathfrak {m}_n$
so that
![]() $\operatorname {ht}\mathfrak {m}_n\geq 2n$
then
$\operatorname {ht}\mathfrak {m}_n\geq 2n$
then
 $$\begin{align*}D_K\left(\bigoplus_n A/\mathfrak{m}_n[-n]\right)\cong \bigoplus_n A/\mathfrak{m}_n[-a_{\mathfrak{m}_n}+n-\operatorname{ht}\mathfrak{m}_n],\end{align*}$$
$$\begin{align*}D_K\left(\bigoplus_n A/\mathfrak{m}_n[-n]\right)\cong \bigoplus_n A/\mathfrak{m}_n[-a_{\mathfrak{m}_n}+n-\operatorname{ht}\mathfrak{m}_n],\end{align*}$$
is not in
![]() $D^-(A)$
; and if we pick
$D^-(A)$
; and if we pick
![]() $\mathfrak {m}_n$
so that
$\mathfrak {m}_n$
so that
![]() $\operatorname {ht}\mathfrak {m}_n> \operatorname {ht}\mathfrak {m}_{n-1}$
then
$\operatorname {ht}\mathfrak {m}_n> \operatorname {ht}\mathfrak {m}_{n-1}$
then
 $$\begin{align*}D_K\left(\bigoplus_n A/\mathfrak{m}_n[-\operatorname{ht}\mathfrak{m}_n]\right)\cong \bigoplus_n A/\mathfrak{m}_n[-a_{\mathfrak{m}_n}],\end{align*}$$
$$\begin{align*}D_K\left(\bigoplus_n A/\mathfrak{m}_n[-\operatorname{ht}\mathfrak{m}_n]\right)\cong \bigoplus_n A/\mathfrak{m}_n[-a_{\mathfrak{m}_n}],\end{align*}$$
is not in
![]() $D_{Coh}(A)$
.
$D_{Coh}(A)$
.
On the other hand,
![]() $D_K(-)$
always map
$D_K(-)$
always map
![]() $D^-(A)$
(resp.
$D^-(A)$
(resp.
![]() $D^-_{Coh}(A)$
) into
$D^-_{Coh}(A)$
) into
![]() $D^+(A)$
(resp.
$D^+(A)$
(resp.
![]() $D^+_{Coh}(A)$
), as this is true for any
$D^+_{Coh}(A)$
), as this is true for any
![]() $K\in D^+(A)$
(resp.
$K\in D^+(A)$
(resp.
![]() $D^+_{Coh}(A)$
).
$D^+_{Coh}(A)$
).
Corollary 4.11. Let A be a Noetherian ring,
![]() $K, K'\in D(A)$
two pseudo-dualizing complexes. Then there exists an invertible object
$K, K'\in D(A)$
two pseudo-dualizing complexes. Then there exists an invertible object
![]() $L\in D(A)$
such that
$L\in D(A)$
such that
![]() $K'\cong K\otimes ^L_A L.$
$K'\cong K\otimes ^L_A L.$
Proof. Let
![]() $L=R\operatorname {Hom}_A(K,K')$
. Then
$L=R\operatorname {Hom}_A(K,K')$
. Then
![]() $L=D_{K'}\circ D_{K}(A)$
is an invertible object by Corollary 4.9 and [25, Tag 0A7E]. The statement that the canonical map
$L=D_{K'}\circ D_{K}(A)$
is an invertible object by Corollary 4.9 and [25, Tag 0A7E]. The statement that the canonical map
![]() $K\otimes ^L_A L\to K'$
is an isomorphism can be checked locally by [25, Tag 0A6A], and when A is local it follows from [25, Tag 0A69].
$K\otimes ^L_A L\to K'$
is an isomorphism can be checked locally by [25, Tag 0A6A], and when A is local it follows from [25, Tag 0A69].
We can characterize the existence of a pseudo-dualizing complex as follows. For finite-dimensional rings this is due to Kawasaki [Reference Kawasaki13].
Theorem 4.12. Let A be a Noetherian ring. Then A admits a pseudo-dualizing complex if and only if there exists a finite type A-algebra B that is Gorenstein and admits a section
![]() $B\to A$
.
$B\to A$
.
Proof. “If” follows from Lemma 4.4.
We proceed to show “only if.” Every finite type A-algebra admits a pseudo-dualizing complex, Corollary 4.5, so we may replace A by any finite type A-algebra that admits a section.
By Remark 4.2, Corollary 4.7, and [25, Tag 0AWY], A is universally catenary, has a codimension function, is Gor-2, and has Gorenstein formal fibers. By [Reference Kawasaki14, p. 2738, proof of Theorem 1.3], there exists a finite type A-algebra B that is Cohen–Macaulay and admits a section. Replace A by B, we may assume our A is Cohen–Macaulay.
Assume A is Cohen–Macaulay. We may assume
![]() $\operatorname {Spec}(A)$
is connected, and K is concentrated in degree
$\operatorname {Spec}(A)$
is connected, and K is concentrated in degree
![]() $0$
. Then the square-zero extension
$0$
. Then the square-zero extension
![]() $A\oplus H^0(K)$
is Gorenstein by [Reference Reiten22] (see also [Reference Aoyama1, Corollary 2.12]), finishing the proof.
$A\oplus H^0(K)$
is Gorenstein by [Reference Reiten22] (see also [Reference Aoyama1, Corollary 2.12]), finishing the proof.
Remark 4.13. Since our A actually has a pseudo-dualizing complex, we can avoid the materials in [Reference Kawasaki14]; the materials in [Reference Kawasaki13] are sufficient with a minor twist. The constructions are the same; [Reference Kawasaki14] proved it works in a greater generality.
5 Formal lifting of pseudo-dualizing complexes
In this section, we prove the following theorem, which, in particular, recovers the existence of dualizing complexes for complete local rings.
Theorem 5.1. Let A be a Noetherian ring, I an ideal of A. Assume that A is I-adically complete. If
![]() $A/I$
admits a pseudo-dualizing (resp. dualizing) complex
$A/I$
admits a pseudo-dualizing (resp. dualizing) complex
![]() $K_1$
, then A admits a pseudo-dualizing (resp. dualizing) complex K such that
$K_1$
, then A admits a pseudo-dualizing (resp. dualizing) complex K such that
![]() $R\operatorname {Hom}_{A}(A/I,K)\cong K_1$
.
$R\operatorname {Hom}_{A}(A/I,K)\cong K_1$
.
Note that this implies A is universally catenary by Corollary 4.7. Compare with [Reference Greco7, Proposition 1.1].
From Lemma 4.4 and Theorem 3.5 we get the following immediate
Corollary 5.2. Let
![]() $(A,I)$
be a Henselian pair where
$(A,I)$
be a Henselian pair where
![]() $(A,\mathfrak {m},k)$
is a Noetherian local ring. Assume that the I-adic completion map
$(A,\mathfrak {m},k)$
is a Noetherian local ring. Assume that the I-adic completion map
![]() $A\to \lim _n A/I^n$
is regular. Then A admits a dualizing complex if and only if
$A\to \lim _n A/I^n$
is regular. Then A admits a dualizing complex if and only if
![]() $A/I$
does.
$A/I$
does.
We need some preparations for Theorem 5.1.
Lemma 5.3. Let A be a Noetherian ring, I an ideal of A. Assume that I is contained in the Jacobson radical of A.
Let
![]() $K\in D^b_{Coh}(A)$
. If
$K\in D^b_{Coh}(A)$
. If
![]() $R\operatorname {Hom}_{A}(A/I,K)$
is a pseudo-dualizing complex for
$R\operatorname {Hom}_{A}(A/I,K)$
is a pseudo-dualizing complex for
![]() $A/I$
, then K is a pseudo-dualizing complex for A.
$A/I$
, then K is a pseudo-dualizing complex for A.
Proof. We may assume
![]() $(A,\mathfrak {m},k)$
local. We have
$(A,\mathfrak {m},k)$
local. We have
is a shift of k, so K is a dualizing complex by [Reference Hartshorne10, Chapter V, Proposition 3.4].
Lemma 5.4. Let A be a Noetherian ring,
![]() $f\in A$
. Let
$f\in A$
. Let
![]() $M\in D^{b}(A)$
. Consider the following conditions.
$M\in D^{b}(A)$
. Consider the following conditions.
-
(i)
 $R\operatorname {Hom}_A(A/fA,M)\in D_{Coh}(A/fA)$
.
$R\operatorname {Hom}_A(A/fA,M)\in D_{Coh}(A/fA)$
. -
(ii)
 $R\operatorname {Hom}_A(\operatorname {Cone}(A\xrightarrow {\times f}A),M)\in D_{Coh}(A/fA)$
.
$R\operatorname {Hom}_A(\operatorname {Cone}(A\xrightarrow {\times f}A),M)\in D_{Coh}(A/fA)$
. -
(iii)
 $M\in D_{Coh}(A)$
.
$M\in D_{Coh}(A)$
.
Then (i) implies (ii), and if A is f-adically complete and M is derived f-adically complete, then (ii) implies (iii).
Proof. Note that
![]() $R\operatorname {Hom}_A(A/fA,M)\in D^+(A/fA)$
since
$R\operatorname {Hom}_A(A/fA,M)\in D^+(A/fA)$
since
![]() $M\in D^+(A)$
. If (i) holds, then
$M\in D^+(A)$
. If (i) holds, then
![]() $R\operatorname {Hom}_A(A/fA,M)\in D^+_{Coh}(A/fA)$
, so for any
$R\operatorname {Hom}_A(A/fA,M)\in D^+_{Coh}(A/fA)$
, so for any
![]() $X\in D^b_{Coh}(A/fA)$
,
$X\in D^b_{Coh}(A/fA)$
,
is in
![]() $D_{Coh}(A/fA)$
, in particular this holds for
$D_{Coh}(A/fA)$
, in particular this holds for
![]() $X=C:=\operatorname {Cone}(A\xrightarrow {\times f}A)$
. Thus (ii) holds.
$X=C:=\operatorname {Cone}(A\xrightarrow {\times f}A)$
. Thus (ii) holds.
Now assume (ii), and assume A is f-adically complete and M is derived f-adically complete. From the distinguished triangle
![]() $A\xrightarrow {\times f} A\to C\to +1$
We know
$A\xrightarrow {\times f} A\to C\to +1$
We know
![]() $R\operatorname {Hom}_A(C,M)\cong \operatorname {Cone}(M\xrightarrow {\times f}M)[-1]$
, so
$R\operatorname {Hom}_A(C,M)\cong \operatorname {Cone}(M\xrightarrow {\times f}M)[-1]$
, so
![]() $\operatorname {Cone}(M\xrightarrow {\times f}M)\in D_{Coh}(A/fA)$
. Let b be an integer such that
$\operatorname {Cone}(M\xrightarrow {\times f}M)\in D_{Coh}(A/fA)$
. Let b be an integer such that
![]() $M\in D^{\leq b}(A)$
. Then
$M\in D^{\leq b}(A)$
. Then
![]() $H^b(M)/fH^b(M)=H^b(\operatorname {Cone}(M\xrightarrow {\times f}M))$
is finite. Thus there exists a finite free A-module F and a map
$H^b(M)/fH^b(M)=H^b(\operatorname {Cone}(M\xrightarrow {\times f}M))$
is finite. Thus there exists a finite free A-module F and a map
![]() $F[-b]\to M$
in
$F[-b]\to M$
in
![]() $D(A)$
inducing a surjective map on
$D(A)$
inducing a surjective map on
![]() $H^b(-)/fH^b(-)$
. Since
$H^b(-)/fH^b(-)$
. Since
![]() $F[-b]$
is also derived f-adically complete [25, Tag 091T], we see
$F[-b]$
is also derived f-adically complete [25, Tag 091T], we see
![]() $F[-b]\to M$
induces a surjective map on
$F[-b]\to M$
induces a surjective map on
![]() $H^b(-)$
by [25, Tag 09B9]. Thus
$H^b(-)$
by [25, Tag 09B9]. Thus
![]() $\operatorname {Cone}(F[-b]\to M)\in D^{\leq b-1}(A)$
, and we see inductively
$\operatorname {Cone}(F[-b]\to M)\in D^{\leq b-1}(A)$
, and we see inductively
![]() $H^c(M)$
is finite for all c.
$H^c(M)$
is finite for all c.
The following two lemmas are not used in the case A, or equivalently
![]() $A/I$
, is finite-dimensional.
$A/I$
, is finite-dimensional.
Lemma 5.5 [Reference Lurie16, Lemma 6.4.3.7 and Proposition 6.6.4.6]
Let A be a Noetherian ring, I a nilpotent ideal of A.
Let
![]() $K\in D^+(A)$
,
$K\in D^+(A)$
,
![]() $L=R\operatorname {Hom}_{A}(A/I,K)$
. Then the followings hold.
$L=R\operatorname {Hom}_{A}(A/I,K)$
. Then the followings hold.
-
(i) If
 $L\in D_{Coh}(A/I)$
, then
$L\in D_{Coh}(A/I)$
, then
 $K\in D_{Coh}(A)$
.
$K\in D_{Coh}(A)$
. -
(ii) If L is a pseudo-dualizing complex for
 $A/I$
, then K is a pseudo-dualizing complex for A.
$A/I$
, then K is a pseudo-dualizing complex for A.
Proof. For (i), we may assume
![]() $I=fA$
principal. Let a be the smallest integer such that
$I=fA$
principal. Let a be the smallest integer such that
![]() $H^a(K)\neq 0$
. Then
$H^a(K)\neq 0$
. Then
![]() $H^a(K)[f]=H^a(L)$
is finite. The exact sequences
$H^a(K)[f]=H^a(L)$
is finite. The exact sequences
![]() $0\to H^a(K)[f]\to H^a(K)[f^{n+1}]\xrightarrow {\times f} H^a(K)[f^n]$
tells us
$0\to H^a(K)[f]\to H^a(K)[f^{n+1}]\xrightarrow {\times f} H^a(K)[f^n]$
tells us
![]() $H^a(K)$
is finite. Apply dimension shifting to the distinguished triangle
$H^a(K)$
is finite. Apply dimension shifting to the distinguished triangle
we see inductively
![]() $H^c(K)$
is finite for all
$H^c(K)$
is finite for all
![]() $c\in \mathbf {Z}$
.
$c\in \mathbf {Z}$
.
For (ii), from Corollary 4.7 we know
![]() $A/I$
is Gor-2, so A is Gor-2 by definition, since I is nilpotent. By Lemma 4.3, it suffices to show (ii) when
$A/I$
is Gor-2, so A is Gor-2 by definition, since I is nilpotent. By Lemma 4.3, it suffices to show (ii) when
![]() $(A,\mathfrak {m},k)$
is local. Then
$(A,\mathfrak {m},k)$
is local. Then
is a shift of k, so K has finite injective dimension [25, Tag 0AVJ], in particular bounded. Since
![]() $K\in D_{Coh}(A)$
by (i), (ii) follows from Lemma 5.3.
$K\in D_{Coh}(A)$
by (i), (ii) follows from Lemma 5.3.
Lemma 5.6. Let A be a Noetherian ring,
![]() $\mathfrak {p}\in \operatorname {Spec}(A),f\in \mathfrak {p}$
. Assume that
$\mathfrak {p}\in \operatorname {Spec}(A),f\in \mathfrak {p}$
. Assume that
![]() $\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Then there exists
$\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Cohen–Macaulay open subscheme. Then there exists
![]() $g\not \in \mathfrak {p}$
such that for all
$g\not \in \mathfrak {p}$
such that for all
![]() $\mathfrak {q}\in V(\mathfrak {p})\cap D(g),$
$\mathfrak {q}\in V(\mathfrak {p})\cap D(g),$
for all
![]() $n\in \mathbf {Z}_{\geq 1}$
.
$n\in \mathbf {Z}_{\geq 1}$
.
Proof. Let
![]() $N\in \mathbf {Z}_{\geq 1}$
be such that
$N\in \mathbf {Z}_{\geq 1}$
be such that
![]() $J:=A[f^\infty ]=A[f^N]$
. After replacing A by some
$J:=A[f^\infty ]=A[f^N]$
. After replacing A by some
![]() $A_g$
, we may assume
$A_g$
, we may assume
![]() $A/\mathfrak {p}$
Cohen–Macaulay and our inequality holds for all
$A/\mathfrak {p}$
Cohen–Macaulay and our inequality holds for all
![]() $\mathfrak {q}\in V(\mathfrak {p})$
and all
$\mathfrak {q}\in V(\mathfrak {p})$
and all
![]() $n< N$
by [Reference Grothendieck8, Proposition 6.10.6]. By the same proposition may also assume that, for all
$n< N$
by [Reference Grothendieck8, Proposition 6.10.6]. By the same proposition may also assume that, for all
![]() $\mathfrak {q}\in V(\mathfrak {p})$
,
$\mathfrak {q}\in V(\mathfrak {p})$
,
![]() $\operatorname {depth} J_{\mathfrak {q}}\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
and
$\operatorname {depth} J_{\mathfrak {q}}\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
and
![]() $\operatorname {depth} (A_{\mathfrak {q}}/J_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})+1$
. Since f is a nonzerodivisor on
$\operatorname {depth} (A_{\mathfrak {q}}/J_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})+1$
. Since f is a nonzerodivisor on
![]() $A/J$
we have
$A/J$
we have
![]() $\operatorname {depth} (A_{\mathfrak {q}}/(f^nA+J)_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
for all
$\operatorname {depth} (A_{\mathfrak {q}}/(f^nA+J)_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
for all
![]() $n\in \mathbf {Z}_{\geq 1}$
.
$n\in \mathbf {Z}_{\geq 1}$
.
For
![]() $n\geq N$
, the sequence
$n\geq N$
, the sequence
is exact. Thus the depth inequalities above imply
![]() $\operatorname {depth} (A_{\mathfrak {q}}/f^nA_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
for all
$\operatorname {depth} (A_{\mathfrak {q}}/f^nA_{\mathfrak {q}})\geq \operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
for all
![]() ${n\in \mathbf {Z}_{\geq N}}$
. Now for all
${n\in \mathbf {Z}_{\geq N}}$
. Now for all
![]() $n\geq N$
we have
$n\geq N$
we have
![]() $ \operatorname {ht}(\mathfrak {q}/f^nA)-\operatorname {depth} \left (A_{\mathfrak {q}}/f^nA_{\mathfrak {q}}\right )\leq \operatorname {ht}(\mathfrak {q})-\operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
. The right-hand side equals
$ \operatorname {ht}(\mathfrak {q}/f^nA)-\operatorname {depth} \left (A_{\mathfrak {q}}/f^nA_{\mathfrak {q}}\right )\leq \operatorname {ht}(\mathfrak {q})-\operatorname {ht}(\mathfrak {q}/\mathfrak {p})$
. The right-hand side equals
![]() $\operatorname {ht}(\mathfrak {p})$
after localization by [Reference Grothendieck8, Proposition 6.10.6].
$\operatorname {ht}(\mathfrak {p})$
after localization by [Reference Grothendieck8, Proposition 6.10.6].
Proof of Theorem 5.1
A pseudo-dualizing complex is a dualizing complex if and only if the ring is finite-dimensional, see Remark 4.2. Since I is in the Jacobson radical of A, A is finite-dimensional if and only if
![]() $A/I$
is. Thus it suffices to prove the result for pseudo-dualizing complexes.
$A/I$
is. Thus it suffices to prove the result for pseudo-dualizing complexes.
We may assume
![]() $I=fA$
principal. Let
$I=fA$
principal. Let
![]() $A_n=A/f^nA$
.
$A_n=A/f^nA$
.
Let
![]() $(J_1^{\bullet },d_1^{\bullet })$
be a bounded below complex of injective
$(J_1^{\bullet },d_1^{\bullet })$
be a bounded below complex of injective
![]() $A_1$
-modules that represents
$A_1$
-modules that represents
![]() $K_1$
. Fix
$K_1$
. Fix
![]() $a\in \mathbf {Z}$
so that
$a\in \mathbf {Z}$
so that
![]() $J_1^m=0$
for all
$J_1^m=0$
for all
![]() $m<a$
. Further, fix
$m<a$
. Further, fix
![]() $c_0\in \mathbf {Z}_{\geq a}$
such that for all minimal primes
$c_0\in \mathbf {Z}_{\geq a}$
such that for all minimal primes
![]() $\mathfrak {q}$
of
$\mathfrak {q}$
of
![]() $fA$
, there exists
$fA$
, there exists
![]() $c\leq c_0$
such that
$c\leq c_0$
such that
![]() $H^c(J_1^{\bullet })_{\mathfrak {q}}\neq 0$
.
$H^c(J_1^{\bullet })_{\mathfrak {q}}\neq 0$
.
For each m, let
![]() $J^m$
be an injective hull of
$J^m$
be an injective hull of
![]() $J_1^m$
as an A-module. Thus
$J_1^m$
as an A-module. Thus
![]() $J^m$
is an essential extension of
$J^m$
is an essential extension of
![]() $J_1^m$
and
$J_1^m$
and
![]() $J_1^m=J^m[f]$
. Let
$J_1^m=J^m[f]$
. Let
![]() $J^m_\infty =J^m[f^\infty ]$
. Then
$J^m_\infty =J^m[f^\infty ]$
. Then
![]() $J^m_\infty $
is an injective A-module by [25, Tag 08XW].
$J^m_\infty $
is an injective A-module by [25, Tag 08XW].
Claim 5.7. There exist maps
![]() $d^m_\infty :J^m_\infty \to J^{m+1}_\infty $
extending
$d^m_\infty :J^m_\infty \to J^{m+1}_\infty $
extending
![]() $d^m_1$
such that
$d^m_1$
such that
![]() $(J^{\bullet }_\infty ,d^{\bullet }_\infty )$
is a complex.
$(J^{\bullet }_\infty ,d^{\bullet }_\infty )$
is a complex.
The proof is given after the main argument. Granting Claim 5.7,
![]() $J^{\bullet }_\infty $
is now a bounded below complex of
$J^{\bullet }_\infty $
is now a bounded below complex of
![]() $f^\infty $
-torsion injective A-modules. We next show that
$f^\infty $
-torsion injective A-modules. We next show that
![]() $J^{\bullet }_\infty \in D(A)$
is bounded. Note that if
$J^{\bullet }_\infty \in D(A)$
is bounded. Note that if
![]() $\dim A_1$
is finite, then
$\dim A_1$
is finite, then
![]() $K_1$
has finite injective dimension, so we could choose
$K_1$
has finite injective dimension, so we could choose
![]() $J_1^{\bullet }$
so that
$J_1^{\bullet }$
so that
![]() $J_1^m=0$
for
$J_1^m=0$
for
![]() $m\gg 1$
, and
$m\gg 1$
, and
![]() $J_\infty $
is automatically bounded. Without this assumption, writing
$J_\infty $
is automatically bounded. Without this assumption, writing
![]() $J^m_n=J^m[f^n]$
, we have that
$J^m_n=J^m[f^n]$
, we have that
![]() $R\operatorname {Hom}_{A_n}(A_1,J^{\bullet }_n)=J^{\bullet }_n[f]=J^{\bullet }_1\in D(A_1)$
, since
$R\operatorname {Hom}_{A_n}(A_1,J^{\bullet }_n)=J^{\bullet }_n[f]=J^{\bullet }_1\in D(A_1)$
, since
![]() $J^{\bullet }_n$
is a bounded below complex of injectives. Thus
$J^{\bullet }_n$
is a bounded below complex of injectives. Thus
![]() $J^{\bullet }_n$
is a pseudo-dualizing complex for
$J^{\bullet }_n$
is a pseudo-dualizing complex for
![]() $A_n$
by Lemma 5.5. Let
$A_n$
by Lemma 5.5. Let
![]() $\mathfrak {q}$
be a minimal prime of
$\mathfrak {q}$
be a minimal prime of
![]() $fA$
. Then
$fA$
. Then
![]() $(J^{\bullet }_n)_{\mathfrak {q}}$
is exact except at a single degree c, and applying
$(J^{\bullet }_n)_{\mathfrak {q}}$
is exact except at a single degree c, and applying
![]() $R\operatorname {Hom}_{A_{\mathfrak {q}}/f^n A_{\mathfrak {q}}}(A_{\mathfrak {q}}/f A_{\mathfrak {q}},-)$
we see
$R\operatorname {Hom}_{A_{\mathfrak {q}}/f^n A_{\mathfrak {q}}}(A_{\mathfrak {q}}/f A_{\mathfrak {q}},-)$
we see
![]() $(J^{\bullet }_1)_{\mathfrak {q}}$
is exact except at degree c, so
$(J^{\bullet }_1)_{\mathfrak {q}}$
is exact except at degree c, so
![]() $c\leq c_0$
. Thus for all
$c\leq c_0$
. Thus for all
![]() $\mathfrak {p}\in V(fA)$
,
$\mathfrak {p}\in V(fA)$
,
![]() $H^c(J^{\bullet }_n)_{\mathfrak {p}}\neq 0$
for some
$H^c(J^{\bullet }_n)_{\mathfrak {p}}\neq 0$
for some
![]() $c\leq c_0$
.
$c\leq c_0$
.
Note that
![]() $A/fA$
is Gor-2 by Corollary 4.7, so Lemma 5.6 shows that there exists
$A/fA$
is Gor-2 by Corollary 4.7, so Lemma 5.6 shows that there exists
![]() $b\in \mathbf {Z}_{\geq 1}$
such that for all
$b\in \mathbf {Z}_{\geq 1}$
such that for all
![]() $\mathfrak {p}\in V(fA)$
and all
$\mathfrak {p}\in V(fA)$
and all
![]() $n\in \mathbf {Z}_{\geq 1}$
,
$n\in \mathbf {Z}_{\geq 1}$
,
Therefore,
![]() $(J^{\bullet }_n)_{\mathfrak {p}}\in D^{[a,b+c_0]}(A)$
, so
$(J^{\bullet }_n)_{\mathfrak {p}}\in D^{[a,b+c_0]}(A)$
, so
![]() $(J^{\bullet }_\infty )_{\mathfrak {p}}\in D^{[a,b+c_0]}(A)$
for all
$(J^{\bullet }_\infty )_{\mathfrak {p}}\in D^{[a,b+c_0]}(A)$
for all
![]() $\mathfrak {p}\in V(fA)$
. Since f is in the Jacobson radical of A we have
$\mathfrak {p}\in V(fA)$
. Since f is in the Jacobson radical of A we have
![]() $J^{\bullet }_\infty \in D^{[a,b+c_0]}(A)$
.
$J^{\bullet }_\infty \in D^{[a,b+c_0]}(A)$
.
Let
![]() $K\in D(A)$
be the derived f-adic completion of
$K\in D(A)$
be the derived f-adic completion of
![]() $J^{\bullet }_\infty $
, so
$J^{\bullet }_\infty $
, so
![]() $K\in D^b(A)$
by for example [25, Tag 091Z]. By [25, Tag 0A6Y] (and [25, Tags 091T and 0A6R]) we have
$K\in D^b(A)$
by for example [25, Tag 091Z]. By [25, Tag 0A6Y] (and [25, Tags 091T and 0A6R]) we have
and the right-hand side is just
![]() $J^{\bullet }_\infty [f]=J^{\bullet }_1$
since
$J^{\bullet }_\infty [f]=J^{\bullet }_1$
since
![]() $J^{\bullet }_\infty $
is a bounded below complex of injectives. Thus
$J^{\bullet }_\infty $
is a bounded below complex of injectives. Thus
![]() $K\in D^b_{Coh}(A)$
by Lemma 5.4. We conclude that K is a pseudo-dualizing complex for A by Lemma 5.3.
$K\in D^b_{Coh}(A)$
by Lemma 5.4. We conclude that K is a pseudo-dualizing complex for A by Lemma 5.3.
Proof of Claim 5.7
We first show that there exist maps
![]() $d^m_2:J^m_2\to J^{m+1}_2$
extending
$d^m_2:J^m_2\to J^{m+1}_2$
extending
![]() $d^m_1$
such that
$d^m_1$
such that
![]() $(J^{\bullet }_2,d^{\bullet }_2)$
is a complex. This follows from the dual version of [25, Tag 0DYR]. We give the proof in our case for the reader’s convenience.
$(J^{\bullet }_2,d^{\bullet }_2)$
is a complex. This follows from the dual version of [25, Tag 0DYR]. We give the proof in our case for the reader’s convenience.
Let
![]() $\delta ^m_2:J^m_2\to J^{m+1}_2$
be arbitrary maps extending
$\delta ^m_2:J^m_2\to J^{m+1}_2$
be arbitrary maps extending
![]() $d^m_1$
. Composing, we get maps
$d^m_1$
. Composing, we get maps
![]() $\delta ^{m+1}_2\circ \delta ^m_2:J^m_2\to J^{m+2}_2$
. Since
$\delta ^{m+1}_2\circ \delta ^m_2:J^m_2\to J^{m+2}_2$
. Since
![]() $(J^{\bullet }_1,d^{\bullet }_1)$
is a complex,
$(J^{\bullet }_1,d^{\bullet }_1)$
is a complex,
![]() $\delta ^{m+1}_2\circ \delta ^m_2$
is zero on
$\delta ^{m+1}_2\circ \delta ^m_2$
is zero on
![]() $J^m_1=J^m_2[f]$
. Since
$J^m_1=J^m_2[f]$
. Since
![]() ${f^2=0\in A_2}$
, we have
${f^2=0\in A_2}$
, we have
![]() $fJ^m_2\subseteq J^m_1$
, so
$fJ^m_2\subseteq J^m_1$
, so
![]() $\operatorname {im}(\delta ^{m+1}_2\circ \delta ^m_2)\subseteq J^{m+2}_1.$
This tells us
$\operatorname {im}(\delta ^{m+1}_2\circ \delta ^m_2)\subseteq J^{m+2}_1.$
This tells us
![]() $(J^{\bullet }_2/J^{\bullet }_1,\delta ^{\bullet }_2)$
is a complex, and that
$(J^{\bullet }_2/J^{\bullet }_1,\delta ^{\bullet }_2)$
is a complex, and that
![]() $\delta ^{m+1}_2\circ \delta ^m_2$
induces a map
$\delta ^{m+1}_2\circ \delta ^m_2$
induces a map
![]() $J^m_2/J^m_1\to J^{m+2}_1$
. It is clear that
$J^m_2/J^m_1\to J^{m+2}_1$
. It is clear that
![]() $\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +2}_1$
is a map of complexes.
$\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +2}_1$
is a map of complexes.
Since
![]() $J^m_2$
is injective, we have canonical isomorphisms
$J^m_2$
is injective, we have canonical isomorphisms
Therefore,
![]() $J^{\bullet }_2/J^{\bullet }_1$
represents
$J^{\bullet }_2/J^{\bullet }_1$
represents
![]() $R\operatorname {Hom}_{A_1}(fA_2,J^{\bullet }_1)$
, so
$R\operatorname {Hom}_{A_1}(fA_2,J^{\bullet }_1)$
, so
![]() $R\operatorname {Hom}_{A_1}(J^{\bullet }_2/J^{\bullet }_1,J^{\bullet +2}_1)=R\operatorname {Hom}_{A_1}(R\operatorname {Hom}_{A_1}(fA_2,J^{\bullet }_1),J^{\bullet }_1[2])=fA_2[2]$
by Corollary 4.9. Thus
$R\operatorname {Hom}_{A_1}(J^{\bullet }_2/J^{\bullet }_1,J^{\bullet +2}_1)=R\operatorname {Hom}_{A_1}(R\operatorname {Hom}_{A_1}(fA_2,J^{\bullet }_1),J^{\bullet }_1[2])=fA_2[2]$
by Corollary 4.9. Thus
![]() $\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +2}_1$
is zero in
$\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +2}_1$
is zero in
![]() $D(A_1),$
hence homotopic to zero (see [25, Tag 05TG]). Let
$D(A_1),$
hence homotopic to zero (see [25, Tag 05TG]). Let
![]() $g^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +1}_1$
be a homotopy between
$g^{\bullet }_2:J^{\bullet }_2/J^{\bullet }_1\to J^{\bullet +1}_1$
be a homotopy between
![]() $\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2$
and
$\delta ^{\bullet +1}_2\circ \delta ^{\bullet }_2$
and
![]() $0$
. View each
$0$
. View each
![]() $g^m_2$
as a map
$g^m_2$
as a map
![]() $g^m_2:J^m_2\to J^{m+1}_2$
, we see
$g^m_2:J^m_2\to J^{m+1}_2$
, we see
![]() $d^m_2=\delta ^m_2-g^m_2$
is what we want.
$d^m_2=\delta ^m_2-g^m_2$
is what we want.
Now
![]() $J^{\bullet }_2$
is a bounded below complex of injective
$J^{\bullet }_2$
is a bounded below complex of injective
![]() $A_2$
-modules, so
$A_2$
-modules, so
thus
![]() $J^{\bullet }_2$
is a pseudo-dualizing complex for
$J^{\bullet }_2$
is a pseudo-dualizing complex for
![]() $A_2$
by Lemma 5.5. The same argument as above tells us we can extend
$A_2$
by Lemma 5.5. The same argument as above tells us we can extend
![]() $d^{\bullet }_2$
to
$d^{\bullet }_2$
to
![]() $d^{\bullet }_3$
, ad infinitum, showing Claim 5.7.
$d^{\bullet }_3$
, ad infinitum, showing Claim 5.7.
Remark 5.8. We record the dual version of [25, Tag 0DYR] in our mind for the reader’s convenience: for a ring A and an ideal I with
![]() $I^2=0$
, the obstruction for a
$I^2=0$
, the obstruction for a
![]() $K\in D^+(A/I)$
to be of the form
$K\in D^+(A/I)$
to be of the form
![]() $R\operatorname {Hom}_A(A/I,K')$
is a map
$R\operatorname {Hom}_A(A/I,K')$
is a map
![]() $R\operatorname {Hom}_{A/I}(I,K)\to K[2]$
in
$R\operatorname {Hom}_{A/I}(I,K)\to K[2]$
in
![]() $D(A/I)$
. The author does not know a reference for this.
$D(A/I)$
. The author does not know a reference for this.
For pseudo-dualizing complexes, this obstruction vanishes automatically by Corollary 4.9, as seen in the proof above. Alternatively, one can use the argument as in [Reference Lurie16, Lemma 6.6.4.9], if willing to use animated rings.
6 Openness of loci
For basics about canonical modules refer to [Reference Aoyama1, §1].
Lemma 6.1. Let A be a Noetherian ring,
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. Assume
$\mathfrak {p}\in \operatorname {Spec}(A)$
. Assume
![]() $\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Gorenstein open subset. Then the followings hold.
$\operatorname {Spec}(A/\mathfrak {p})$
contains a nonempty Gorenstein open subset. Then the followings hold.
-
(i) Let
 $K\in D^b_{Coh}(A)$
. If
$K\in D^b_{Coh}(A)$
. If
 $K_{\mathfrak {p}}$
is a dualizing complex for
$K_{\mathfrak {p}}$
is a dualizing complex for
 $A_{\mathfrak {p}}$
, then there exists an
$A_{\mathfrak {p}}$
, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $K_{\mathfrak {q}}$
is a dualizing complex for
$K_{\mathfrak {q}}$
is a dualizing complex for
 $A_{\mathfrak {q}}$
for all
$A_{\mathfrak {q}}$
for all
 $\mathfrak {q}\in V(\mathfrak {p})\cap D(f)$
.
$\mathfrak {q}\in V(\mathfrak {p})\cap D(f)$
. -
(ii) Let M be a finite A-module. If
 $M_{\mathfrak {p}}$
is a canonical module for
$M_{\mathfrak {p}}$
is a canonical module for
 $A_{\mathfrak {p}}$
, then there exists an
$A_{\mathfrak {p}}$
, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $M_{\mathfrak {q}}$
is a canonical module for
$M_{\mathfrak {q}}$
is a canonical module for
 $A_{\mathfrak {q}}$
for all
$A_{\mathfrak {q}}$
for all
 $\mathfrak {q}\in V(\mathfrak {p})\cap D(f)$
.
$\mathfrak {q}\in V(\mathfrak {p})\cap D(f)$
.
Proof. We may assume
![]() $A/\mathfrak {p}$
Gorenstein. Let B be the
$A/\mathfrak {p}$
Gorenstein. Let B be the
![]() $\mathfrak {p}$
-adic completion of A, so
$\mathfrak {p}$
-adic completion of A, so
![]() $A\to B$
is a flat ring map with
$A\to B$
is a flat ring map with
![]() $A/\mathfrak {p}=B/\mathfrak {p} B$
, thus open subsets of
$A/\mathfrak {p}=B/\mathfrak {p} B$
, thus open subsets of
![]() $V(\mathfrak {p})$
in
$V(\mathfrak {p})$
in
![]() $\operatorname {Spec}(A)$
are in one-to-one correspondence with open subsets of
$\operatorname {Spec}(A)$
are in one-to-one correspondence with open subsets of
![]() $V(\mathfrak {p} B)$
in
$V(\mathfrak {p} B)$
in
![]() $\operatorname {Spec}(B)$
. Note that for all
$\operatorname {Spec}(B)$
. Note that for all
![]() $\mathfrak {P}\in V(\mathfrak {p})$
,
$\mathfrak {P}\in V(\mathfrak {p})$
,
![]() $A_{\mathfrak {P}}^\wedge =B_{\mathfrak {P} B}^\wedge $
since
$A_{\mathfrak {P}}^\wedge =B_{\mathfrak {P} B}^\wedge $
since
![]() $A/\mathfrak {p}^n=B/\mathfrak {p}^n B$
for all n. Thus, the base change of a dualizing complex for (resp. canonical module of)
$A/\mathfrak {p}^n=B/\mathfrak {p}^n B$
for all n. Thus, the base change of a dualizing complex for (resp. canonical module of)
![]() $A_{\mathfrak {p}}$
to
$A_{\mathfrak {p}}$
to
![]() $B_{\mathfrak {p} B}$
is a dualizing complex for (resp. canonical module of)
$B_{\mathfrak {p} B}$
is a dualizing complex for (resp. canonical module of)
![]() $B_{\mathfrak {p} B}$
, and we may apply flat descent ([25, Tag 0E4A] and [Reference Aoyama1, Theorem 4.2]) for
$B_{\mathfrak {p} B}$
, and we may apply flat descent ([25, Tag 0E4A] and [Reference Aoyama1, Theorem 4.2]) for
![]() $\mathfrak {P}\in V(\mathfrak {p})$
. Thus it suffices to prove the lemma in the case A is
$\mathfrak {P}\in V(\mathfrak {p})$
. Thus it suffices to prove the lemma in the case A is
![]() $\mathfrak {p}$
-adically complete and
$\mathfrak {p}$
-adically complete and
![]() $A/\mathfrak {p}$
is Gorenstein.
$A/\mathfrak {p}$
is Gorenstein.
In this case, A admits a pseudo-dualizing complex E by Theorem 5.1, and we have
![]() $K_{\mathfrak {p}}\cong E_{\mathfrak {p}}$
(resp.
$K_{\mathfrak {p}}\cong E_{\mathfrak {p}}$
(resp.
![]() $M_{\mathfrak {p}}\cong H^0(E_{\mathfrak {p}})$
and
$M_{\mathfrak {p}}\cong H^0(E_{\mathfrak {p}})$
and
![]() $E_{\mathfrak {p}}\in D^{\geq 0}(A_{\mathfrak {p}})$
; [Reference Aoyama1, (1.5)]) after a shift. After localizing we have
$E_{\mathfrak {p}}\in D^{\geq 0}(A_{\mathfrak {p}})$
; [Reference Aoyama1, (1.5)]) after a shift. After localizing we have
![]() $K\cong E$
by Lemma 2.1 (resp.
$K\cong E$
by Lemma 2.1 (resp.
![]() $M\cong H^0(E)$
and
$M\cong H^0(E)$
and
![]() $E\in D^{\geq 0}(A)$
), as desired.
$E\in D^{\geq 0}(A)$
), as desired.
We say a finite module M over a Noetherian ring A a canonical module if
![]() $M_{\mathfrak {p}}$
is a canonical module of A for all
$M_{\mathfrak {p}}$
is a canonical module of A for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. Localization of a canonical module is a canonical module, see [Reference Aoyama1, Corollary 4.3], so it suffices to check at the maximal ideals of A.
$\mathfrak {p}\in \operatorname {Spec}(A)$
. Localization of a canonical module is a canonical module, see [Reference Aoyama1, Corollary 4.3], so it suffices to check at the maximal ideals of A.
Theorem 6.2. Let A be a Noetherian ring that is Gor-2. Then the followings hold.
-
(i) If
 $\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
$\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
 $A_{\mathfrak {p}}$
admits a dualizing complex, then there exists an
$A_{\mathfrak {p}}$
admits a dualizing complex, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $A_f$
admits a pseudo-dualizing complex.
$A_f$
admits a pseudo-dualizing complex. -
(ii) Let
 $K\in D^b_{Coh}(A)$
. If
$K\in D^b_{Coh}(A)$
. If
 $\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
$\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
 $K_{\mathfrak {p}}$
is a dualizing complex for
$K_{\mathfrak {p}}$
is a dualizing complex for
 $A_{\mathfrak {p}}$
, then there exists an
$A_{\mathfrak {p}}$
, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $K_f$
is a pseudo-dualizing complex for
$K_f$
is a pseudo-dualizing complex for
 $A_f$
.
$A_f$
. -
(iii) If
 $\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
$\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
 $A_{\mathfrak {p}}$
admits a canonical module, then there exists an
$A_{\mathfrak {p}}$
admits a canonical module, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $A_f$
admits a canonical module.
$A_f$
admits a canonical module. -
(iv) Let M be a finite A-module. If
 $\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
$\mathfrak {p}\in \operatorname {Spec}(A)$
is such that
 $M_{\mathfrak {p}}$
is a canonical module of
$M_{\mathfrak {p}}$
is a canonical module of
 $A_{\mathfrak {p}}$
, then there exists an
$A_{\mathfrak {p}}$
, then there exists an
 $f\in A\setminus \mathfrak {p}$
such that
$f\in A\setminus \mathfrak {p}$
such that
 $M_f$
is a canonical module of
$M_f$
is a canonical module of
 $A_f$
.
$A_f$
.
Proof. We know (ii) implies (i) and (iv) implies (iii) by Lemma 2.2. On the other hand, (ii) and (iv) follows from Lemma 6.1 and general topology [25, Tag 0541].
Apply to the case
![]() $K=A$
and
$K=A$
and
![]() $M=A$
, we get the following. The Gorenstein case is [Reference Greco and Marinari6, Proposition 1.7], but the quasi-Gorenstein case seems to be new.
$M=A$
, we get the following. The Gorenstein case is [Reference Greco and Marinari6, Proposition 1.7], but the quasi-Gorenstein case seems to be new.
Corollary 6.3. The Gorenstein and quasi-Gorenstein loci of a Gor-2 Noetherian ring is open.
Remark 6.4. If we assume in addition that A is Cohen–Macaulay, then Theorem 6.2 follows from the characterization of canonical modules [Reference Reiten22] (see also [Reference Aoyama1, Corollary 2.12]) and [Reference Greco and Marinari6, Proposition 1.7].
Theorem 6.5. Let A be a Noetherian ring (resp. a Noetherian ring of finite dimension). Assume
-
1. A is a G-ring.
-
2. A is Gor-2.
Then there exists a faithfully flat, étale ring map
![]() $A\to A'$
such that
$A\to A'$
such that
![]() $A'$
admits a pseudo-dualizing complex (resp. a dualizing complex).
$A'$
admits a pseudo-dualizing complex (resp. a dualizing complex).
Proof. Let
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
. By Corollary 3.6, there exists an étale ring map
$\mathfrak {p}\in \operatorname {Spec}(A)$
. By Corollary 3.6, there exists an étale ring map
![]() $A\to B$
and a prime
$A\to B$
and a prime
![]() $\mathfrak {q}\in \operatorname {Spec}(B)$
lying above
$\mathfrak {q}\in \operatorname {Spec}(B)$
lying above
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $B_{\mathfrak {q}}$
admits a dualizing complex. Note that B is Gor-2 since it is of finite type over A, Corollary 4.8. By Theorem 6.2, localizing B near
$B_{\mathfrak {q}}$
admits a dualizing complex. Note that B is Gor-2 since it is of finite type over A, Corollary 4.8. By Theorem 6.2, localizing B near
![]() $\mathfrak {q}$
we may assume B admits a pseudo-dualizing complex. If A is finite-dimensional then so is B, so B admits a dualizing complex. Now we take
$\mathfrak {q}$
we may assume B admits a pseudo-dualizing complex. If A is finite-dimensional then so is B, so B admits a dualizing complex. Now we take
![]() $A'$
to be a finite product of such B so that
$A'$
to be a finite product of such B so that
![]() $\operatorname {Spec}(A')\to \operatorname {Spec}(A)$
is surjective.
$\operatorname {Spec}(A')\to \operatorname {Spec}(A)$
is surjective.
Corollary 6.6. Let A be a Noetherian quasi-excellent ring. Then there exists a faithfully flat, étale ring map
![]() $A\to A'$
such that
$A\to A'$
such that
![]() $A'$
is excellent.
$A'$
is excellent.
Remark 6.7. Corollary 6.6 is not difficult by itself and may be well known. We sketch an argument. First, consider a finite injective map
![]() $A\to B$
of Noetherian domains with B universally catenary. Then for
$A\to B$
of Noetherian domains with B universally catenary. Then for
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
,
$\mathfrak {p}\in \operatorname {Spec}(A)$
,
![]() $A_{\mathfrak {p}}$
is universally catenary if and only if for all
$A_{\mathfrak {p}}$
is universally catenary if and only if for all
![]() $\mathfrak {q}\in \operatorname {Spec}(B)$
above
$\mathfrak {q}\in \operatorname {Spec}(B)$
above
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() $\operatorname {ht}(\mathfrak {q})=\operatorname {ht}(\mathfrak {p})$
. This follows from [25, Tags 02IJ and 0AW6]. This condition is constructible by for example [Reference Grothendieck8, Proposition 6.10.6].
$\operatorname {ht}(\mathfrak {q})=\operatorname {ht}(\mathfrak {p})$
. This follows from [25, Tags 02IJ and 0AW6]. This condition is constructible by for example [Reference Grothendieck8, Proposition 6.10.6].
Since a normal quasi-excellent ring is universally catenary [25, Tag 0AW6], and since a quasi-excellent ring is Nagata [25, Tag 07QV], we can take B to be the normalization of
![]() $A=R/\mathfrak {p}$
where
$A=R/\mathfrak {p}$
where
![]() $\mathfrak {p}$
is a minimal prime of a given quasi-excellent ring R. It is now clear that the universally catenary locus of a quasi-excellent ring is open, and that a unibranch quasi-excellent local ring is universally catenary. We thus get Corollary 6.6 from [25, Tag 0CB4].
$\mathfrak {p}$
is a minimal prime of a given quasi-excellent ring R. It is now clear that the universally catenary locus of a quasi-excellent ring is open, and that a unibranch quasi-excellent local ring is universally catenary. We thus get Corollary 6.6 from [25, Tag 0CB4].
Using [Reference Česnavičius3, Lemma 2.5 and Theorem 2.13], replacing normalization with an
![]() $(S_2)$
-ification, the argument above tells us that every
$(S_2)$
-ification, the argument above tells us that every
![]() $(S_2)$
-quasi-excellent [Reference Česnavičius3, (2.12)] Noetherian ring A has open universally catenary locus and admits an étale, faithfully flat ring map
$(S_2)$
-quasi-excellent [Reference Česnavičius3, (2.12)] Noetherian ring A has open universally catenary locus and admits an étale, faithfully flat ring map
![]() $A\to A'$
such that
$A\to A'$
such that
![]() $A'$
is
$A'$
is
![]() $(S_2)$
-excellent; and a Noetherian unibranch local ring with
$(S_2)$
-excellent; and a Noetherian unibranch local ring with
![]() $(S_2)$
formal fibers is universally catenary.
$(S_2)$
formal fibers is universally catenary.
7 One-dimensional schemes
Lemma 7.1. Let
![]() $(A,\mathfrak {m},k)\to (B,\mathfrak {n},l)$
be a flat local map of Noetherian local rings. Assume that A admits a dualizing complex K, and that
$(A,\mathfrak {m},k)\to (B,\mathfrak {n},l)$
be a flat local map of Noetherian local rings. Assume that A admits a dualizing complex K, and that
![]() $B/\mathfrak {m} B$
is Gorenstein. Then
$B/\mathfrak {m} B$
is Gorenstein. Then
![]() $K\otimes _A^L B$
is a dualizing complex for B.
$K\otimes _A^L B$
is a dualizing complex for B.
Proof.
![]() $R\operatorname {Hom}_A(k,K)$
is a shift of k, so
$R\operatorname {Hom}_A(k,K)$
is a shift of k, so
![]() $R\operatorname {Hom}_B(B/\mathfrak {m} B,K\otimes _A^L B)$
is a shift of
$R\operatorname {Hom}_B(B/\mathfrak {m} B,K\otimes _A^L B)$
is a shift of
![]() $B/\mathfrak {m} B$
by [25, Tag 0A6A]. We conclude by Lemma 5.3.
$B/\mathfrak {m} B$
by [25, Tag 0A6A]. We conclude by Lemma 5.3.
Lemma 7.2. Let A be a Noetherian local ring of dimension 1. Assume that the formal fibers of A are Gorenstein. Then A admits a dualizing complex.
Proof. Let a be a parameter of A. The
![]() $aA$
-adic completion
$aA$
-adic completion
![]() $A^\wedge $
of A is a complete local ring, thus admits a normalized dualizing complex M.
$A^\wedge $
of A is a complete local ring, thus admits a normalized dualizing complex M.
Let E be a dualizing complex for the Artinian ring
![]() $A_a$
concentrated in degree
$A_a$
concentrated in degree
![]() $-1$
. The map
$-1$
. The map
![]() $A_a\to (A^\wedge )_a$
is a flat map between Artinian rings with Gorenstein fibers by our assumptions, thus
$A_a\to (A^\wedge )_a$
is a flat map between Artinian rings with Gorenstein fibers by our assumptions, thus
![]() $E\otimes ^L_{A_a}(A^\wedge )_a$
is a dualizing complex by Lemma 7.1. On the other hand
$E\otimes ^L_{A_a}(A^\wedge )_a$
is a dualizing complex by Lemma 7.1. On the other hand
![]() $M_a$
is another dualizing complex of
$M_a$
is another dualizing complex of
![]() $(A^\wedge )_a$
concentrated in degree
$(A^\wedge )_a$
concentrated in degree
![]() $-1$
by [25, Tag 0A7V]. Thus
$-1$
by [25, Tag 0A7V]. Thus
![]() $ E\otimes ^L_{A_a}(A^\wedge )_a\cong M_a $
as
$ E\otimes ^L_{A_a}(A^\wedge )_a\cong M_a $
as
![]() $(A^\wedge )_a$
is Artinian. By [Reference Bhatt2, Theorem 1.4], there exists
$(A^\wedge )_a$
is Artinian. By [Reference Bhatt2, Theorem 1.4], there exists
![]() $K\in D(A)$
such that
$K\in D(A)$
such that
![]() $K\otimes ^L_A A^\wedge \cong M$
. Then K is a dualizing complex for A [25, Tag 0E4A].
$K\otimes ^L_A A^\wedge \cong M$
. Then K is a dualizing complex for A [25, Tag 0E4A].
Remark 7.3. Lemma 7.2 also follows from [Reference Fossum, Foxby, Griffith and Reiten4, Theorem 5.3] and, say, [Reference Ogoma21, Corollary 3.7].
Theorem 7.4. Let X be a Noetherian scheme. Assume the followings.
-
1. X is Gor-2.
-
2. Every local ring of X of dimension 1 has Gorenstein formal fibers.
Let U be an open subscheme of X, K a pseudo-dualizing complex on U such that for all generic points
![]() $\xi \in U$
,
$\xi \in U$
,
![]() $K_\xi $
is concentrated in degree
$K_\xi $
is concentrated in degree
![]() $0$
(for example
$0$
(for example
![]() $U=\emptyset $
). Then there exists an open subset
$U=\emptyset $
). Then there exists an open subset
![]() $W\supseteq U$
of X such that
$W\supseteq U$
of X such that
![]() $\dim \mathcal {O}_{X,x}>1$
for all
$\dim \mathcal {O}_{X,x}>1$
for all
![]() $x\not \in W$
and that W admits a pseudo-dualizing complex
$x\not \in W$
and that W admits a pseudo-dualizing complex
![]() $K_W$
with
$K_W$
with
![]() $K_W|_{U}=K$
such that
$K_W|_{U}=K$
such that
![]() $K_\xi $
is concentrated in degree
$K_\xi $
is concentrated in degree
![]() $0$
for all generic points
$0$
for all generic points
![]() $\xi \in X$
.
$\xi \in X$
.
Proof. We may assume
![]() $(U,K)$
cannot be enlarged to any
$(U,K)$
cannot be enlarged to any
![]() $(W,K_W)$
, and we shall show
$(W,K_W)$
, and we shall show
![]() $\dim \mathcal {O}_{X,x}>1$
for all
$\dim \mathcal {O}_{X,x}>1$
for all
![]() $x\not \in U$
.
$x\not \in U$
.
Let
![]() $x\not \in U$
, and assume
$x\not \in U$
, and assume
![]() $\dim \mathcal {O}_{X,x}\leq 1$
. Let
$\dim \mathcal {O}_{X,x}\leq 1$
. Let
![]() $V=\operatorname {Spec}(A)$
be an affine open neighborhood of
$V=\operatorname {Spec}(A)$
be an affine open neighborhood of
![]() $x\in X$
such that A has a pseudo-dualizing complex L, which exists by Lemma 7.2 and Theorem 6.2. We may assume that all generic points of V specialize to x. Since
$x\in X$
such that A has a pseudo-dualizing complex L, which exists by Lemma 7.2 and Theorem 6.2. We may assume that all generic points of V specialize to x. Since
![]() $\dim \mathcal {O}_{X,x}=1$
, we see from [25, Tag 0A7V] that, after shifting, we may assume
$\dim \mathcal {O}_{X,x}=1$
, we see from [25, Tag 0A7V] that, after shifting, we may assume
![]() $L_{\mathfrak {q}}$
is concentrated at degree
$L_{\mathfrak {q}}$
is concentrated at degree
![]() $0$
for all minimal primes
$0$
for all minimal primes
![]() $\mathfrak {q}$
of A.
$\mathfrak {q}$
of A.
If
![]() $U\times _X \operatorname {Spec}(\mathcal {O}_{X,x})$
is empty, then we may assume
$U\times _X \operatorname {Spec}(\mathcal {O}_{X,x})$
is empty, then we may assume
![]() $U\cap V=\emptyset $
, so we can enlarge U to
$U\cap V=\emptyset $
, so we can enlarge U to
![]() $U\cup V$
. Otherwise
$U\cup V$
. Otherwise
![]() $U\times _X \operatorname {Spec}(\mathcal {O}_{X,x})$
has dimension zero, so it is affine. Thus, we may assume
$U\times _X \operatorname {Spec}(\mathcal {O}_{X,x})$
has dimension zero, so it is affine. Thus, we may assume
![]() $U\cap V$
is affine by [25, Tag 01Z6]. Write
$U\cap V$
is affine by [25, Tag 01Z6]. Write
![]() $B=\mathcal {O}(U\cap V)$
, so B admits a dualizing complex
$B=\mathcal {O}(U\cap V)$
, so B admits a dualizing complex
![]() $K_0$
given by the restriction of K to
$K_0$
given by the restriction of K to
![]() $U\cap V$
. Then
$U\cap V$
. Then
![]() $L\otimes ^L_{A}B_{\mathfrak {p}}\cong K_0\otimes ^L_B B_{\mathfrak {p}}$
, where
$L\otimes ^L_{A}B_{\mathfrak {p}}\cong K_0\otimes ^L_B B_{\mathfrak {p}}$
, where
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
corresponds to x, since
$\mathfrak {p}\in \operatorname {Spec}(A)$
corresponds to x, since
![]() $\dim B_{\mathfrak {p}}=0$
and both sides are dualizing complexes concentrated in degree
$\dim B_{\mathfrak {p}}=0$
and both sides are dualizing complexes concentrated in degree
![]() $0$
. Thus there exists
$0$
. Thus there exists
![]() $g\in A\setminus \mathfrak {p}$
such that
$g\in A\setminus \mathfrak {p}$
such that
![]() $L\otimes ^L_{A} B_{g}\cong K_0\otimes ^L_B B_{g}$
by Lemma 2.1, so we can enlarge U to
$L\otimes ^L_{A} B_{g}\cong K_0\otimes ^L_B B_{g}$
by Lemma 2.1, so we can enlarge U to
![]() $U\cup \operatorname {Spec}(A_g)$
.
$U\cup \operatorname {Spec}(A_g)$
.
Remark 7.5. The ring
![]() $A/I$
in [Reference Greco7, §1] does not admit a dualizing complex by Theorem 5.1.
$A/I$
in [Reference Greco7, §1] does not admit a dualizing complex by Theorem 5.1.
![]() $A/I$
is a semi-local ring with two maximal ideals
$A/I$
is a semi-local ring with two maximal ideals
![]() $\mathfrak {m}',\mathfrak {n}'$
with
$\mathfrak {m}',\mathfrak {n}'$
with
![]() $\operatorname {ht}(\mathfrak {m}')=1$
,
$\operatorname {ht}(\mathfrak {m}')=1$
,
![]() $\operatorname {ht}(\mathfrak {n}')=2$
. Both localizations
$\operatorname {ht}(\mathfrak {n}')=2$
. Both localizations
![]() $(A/I)_{\mathfrak {m}'}$
and
$(A/I)_{\mathfrak {m}'}$
and
![]() $(A/I)_{\mathfrak {n}'}$
admit dualizing complexes, see [Reference Greco7, Lemma 1.5], but the restrictions of a dualizing complex for
$(A/I)_{\mathfrak {n}'}$
admit dualizing complexes, see [Reference Greco7, Lemma 1.5], but the restrictions of a dualizing complex for
![]() $(A/I)_{\mathfrak {n}'}$
to the generic points are concentrated in different degrees by [25, Tag 0A7V], so Theorem 7.4 does not apply. Together with Theorem 6.2, this tells us that admitting dualizing complexes is not a Zariski local property.
$(A/I)_{\mathfrak {n}'}$
to the generic points are concentrated in different degrees by [25, Tag 0A7V], so Theorem 7.4 does not apply. Together with Theorem 6.2, this tells us that admitting dualizing complexes is not a Zariski local property.
Corollary 7.6. Let X be a Noetherian scheme of dimension 1. Then X admits a dualizing complex if and only if X is Gor-2 and the local rings of X has Gorenstein formal fibers.
Proof. “Only if” follows from [25, Tag 0AWY] and Corollary 4.7. “If” follows from Theorem 7.4 with
![]() $U=\emptyset $
.
$U=\emptyset $
.
Remark 7.7. There exists a Noetherian local domain of dimension
![]() $1$
with non-Gorenstein formal fibers, see [Reference Ferrand and Raynaud5, Remarque 3.2]. Such a ring is Gor-2, and even J-2, being one-dimensional and local.
$1$
with non-Gorenstein formal fibers, see [Reference Ferrand and Raynaud5, Remarque 3.2]. Such a ring is Gor-2, and even J-2, being one-dimensional and local.
There also exists a one-dimensional G-ring that is not Gor-2. Such a ring can be constructed using the general method in [Reference Hochster12].
Therefore, neither of the two conditions in Corollary 7.6 implies the other.
Remark 7.8. In the terminology of [Reference Sharp24], Corollary 7.6 says that a Noetherian scheme of dimension 1 admits a dualizing complex if and only if it is acceptable.
Remark 7.9. There exists a two-dimensional excellent local UFD that does not admit a dualizing complex. See [Reference Nishimura20, Example 6.1].
8 Remarks on quotients of Gorenstein and Cohen–Macaulay rings
Our Lemma 4.4 and Theorem 4.12 imply the following result, originally due to Kawasaki [Reference Kawasaki13] for finite-dimensional rings.
Theorem 8.1. Let A be a Noetherian ring. Then the followings are equivalent.
-
(i) A is a quotient of a Gorenstein ring.
-
(ii) There exists a finitely generated A-algebra B that is Gorenstein and admits a section
 $B\to A$
.
$B\to A$
. -
(iii) A admits a pseudo-dualizing complex.
Therefore, Theorem 5.1 can be rewritten as
Theorem 8.2. Let A be a Noetherian ring, I an ideal of A. If A is I-adically complete, then
![]() $A/I$
is a quotient of a Gorenstein ring if and only if A is.
$A/I$
is a quotient of a Gorenstein ring if and only if A is.
On the other hand, quotients of Cohen–Macaulay rings were also studied by Kawasaki [Reference Kawasaki14]. Note that the conditions (C1)-(C3) there are equivalent to CM-excellence as in [Reference Česnavičius3, Definition 1.2] (cf. [Reference Česnavičius3, Remark 1.5]). Therefore, [Reference Kawasaki14, Theorem 1.3] and its proof tell us the following.
Theorem 8.3. Let A be a Noetherian ring. Then the followings are equivalent.
-
(i) A is a quotient of a Cohen–Macaulay ring.
-
(ii) There exists a finitely generated A-algebra B that is Cohen–Macaulay and admits a section
 $B\to A$
.
$B\to A$
. -
(iii) A is CM-excellent and admits a codimension function.
Pham Hung Quy asks the author if the analog of Theorem 8.2 holds for Cohen–Macaulay instead of Gorenstein. We can answer this question affirmatively under some additional assumptions.
Theorem 8.4. Let A be a Noetherian ring, I an ideal of A. Assume that
![]() $A/I$
is either quasi-excellent, or semilocal and Nagata. If A is I-adically complete, then
$A/I$
is either quasi-excellent, or semilocal and Nagata. If A is I-adically complete, then
![]() $A/I$
is a quotient of a Cohen–Macaulay ring if and only if A is.
$A/I$
is a quotient of a Cohen–Macaulay ring if and only if A is.
We need two lemmas for Theorem 8.4.
Lemma 8.5. Let A be a Noetherian ring, I an ideal of A. Assume that the pair
![]() $(A,I)$
is Henselian.
$(A,I)$
is Henselian.
Assume that A is catenary, and that
![]() $A/I$
admits a codimension function
$A/I$
admits a codimension function
![]() $c:\operatorname {Spec}(A/I)\to \mathbf {Z}$
. For
$c:\operatorname {Spec}(A/I)\to \mathbf {Z}$
. For
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
and
$\mathfrak {p}\in \operatorname {Spec}(A)$
and
![]() $Q\in V(I)$
containing
$Q\in V(I)$
containing
![]() $\mathfrak {p}$
, let
$\mathfrak {p}$
, let
![]() $c(\mathfrak {p},Q)=c(Q/I)-\operatorname {ht}(Q/\mathfrak {p})$
. Then the followings hold.
$c(\mathfrak {p},Q)=c(Q/I)-\operatorname {ht}(Q/\mathfrak {p})$
. Then the followings hold.
-
(i) For every
 $\mathfrak {p}\in \operatorname {Spec}(A)$
,
$\mathfrak {p}\in \operatorname {Spec}(A)$
,
 $c(\mathfrak {p},Q)$
is independent of the choice of Q.
$c(\mathfrak {p},Q)$
is independent of the choice of Q. -
(ii) The assignment
 $\mathfrak {p}\mapsto c(\mathfrak {p},Q)$
, where
$\mathfrak {p}\mapsto c(\mathfrak {p},Q)$
, where
 $Q\in V(I+\mathfrak {p})$
is arbitrary, is a codimension function on A.
$Q\in V(I+\mathfrak {p})$
is arbitrary, is a codimension function on A.
Proof. Since
![]() $c(-)$
is a codimension function of
$c(-)$
is a codimension function of
![]() $A/I$
, for
$A/I$
, for
![]() $Q\subseteq Q'\in V(I+\mathfrak {p})$
, we have
$Q\subseteq Q'\in V(I+\mathfrak {p})$
, we have
![]() $c(\mathfrak {p},Q')-c(\mathfrak {p},Q)=\operatorname {ht}(Q'/Q)+\operatorname {ht}(Q/\mathfrak {p})-\operatorname {ht}(Q'/\mathfrak {p})$
. Since A is catenary, the number on the right-hand side is
$c(\mathfrak {p},Q')-c(\mathfrak {p},Q)=\operatorname {ht}(Q'/Q)+\operatorname {ht}(Q/\mathfrak {p})-\operatorname {ht}(Q'/\mathfrak {p})$
. Since A is catenary, the number on the right-hand side is
![]() $0$
. Thus for
$0$
. Thus for
![]() $Q\subseteq Q'\in V(I+\mathfrak {p})$
, we have
$Q\subseteq Q'\in V(I+\mathfrak {p})$
, we have
![]() $c(\mathfrak {p},Q')=c(\mathfrak {p},Q)$
. Since
$c(\mathfrak {p},Q')=c(\mathfrak {p},Q)$
. Since
![]() $(A,I)$
is Henselian,
$(A,I)$
is Henselian,
![]() $V(I+\mathfrak {p})$
is connected, see [25, Tag 09Y6]. This shows (i). For (ii), note that
$V(I+\mathfrak {p})$
is connected, see [25, Tag 09Y6]. This shows (i). For (ii), note that
![]() $V(I+\mathfrak {p})$
is nonempty for all
$V(I+\mathfrak {p})$
is nonempty for all
![]() $\mathfrak {p}\in \operatorname {Spec}(A)$
, so our function is well defined. To show it is a codimension function, it suffices to show for
$\mathfrak {p}\in \operatorname {Spec}(A)$
, so our function is well defined. To show it is a codimension function, it suffices to show for
![]() $\mathfrak {p}\subseteq \mathfrak {p}'\subseteq Q$
where
$\mathfrak {p}\subseteq \mathfrak {p}'\subseteq Q$
where
![]() $Q\in V(I)$
, we have
$Q\in V(I)$
, we have
![]() $c(\mathfrak {p}',Q)-c(\mathfrak {p},Q)=\operatorname {ht}(\mathfrak {p}'/\mathfrak {p})$
. This is clear as A is catenary.
$c(\mathfrak {p}',Q)-c(\mathfrak {p},Q)=\operatorname {ht}(\mathfrak {p}'/\mathfrak {p})$
. This is clear as A is catenary.
Lemma 8.6. Let A be a Noetherian ring, I an ideal of A. Assume that the pair
![]() $(A,I)$
is Henselian.
$(A,I)$
is Henselian.
Assume the followings hold.
-
(i) For every minimal prime
 $\mathfrak {p}$
of A, there exists a finite injective ring map
$\mathfrak {p}$
of A, there exists a finite injective ring map
 $A/\mathfrak {p}\to B$
such that B is universally catenary.
$A/\mathfrak {p}\to B$
such that B is universally catenary. -
(ii)
 $A/I$
is universally catenary and admits a codimension function.
$A/I$
is universally catenary and admits a codimension function.
Then A is universally catenary and admits a codimension function.
Proof. By Lemma 8.5, it suffices to show A is universally catenary. We may, therefore, assume A is an integral domain and there exists a finite injective ring map
![]() $A\to B$
such that B is universally catenary. We may also assume B is an integral domain. Let
$A\to B$
such that B is universally catenary. We may also assume B is an integral domain. Let
![]() $c:\operatorname {Spec}(A/I)\to \mathbf {Z}$
be a codimension function. Let
$c:\operatorname {Spec}(A/I)\to \mathbf {Z}$
be a codimension function. Let
![]() $\delta (Q)=c((Q\cap A)/I)-\operatorname {ht}(Q)$
for
$\delta (Q)=c((Q\cap A)/I)-\operatorname {ht}(Q)$
for
![]() $Q\in V(IB)$
. For
$Q\in V(IB)$
. For
![]() $Q\subseteq Q'\in V(IB)$
, we have
$Q\subseteq Q'\in V(IB)$
, we have
 $$ \begin{align*} c((Q'\cap A)/I)-c((Q\cap A)/I)&=\operatorname{ht}((Q'\cap A)/(Q\cap A))\\ &=\operatorname{ht}(Q'/Q)\\ &=\operatorname{ht}(Q')-\operatorname{ht}(Q), \end{align*} $$
$$ \begin{align*} c((Q'\cap A)/I)-c((Q\cap A)/I)&=\operatorname{ht}((Q'\cap A)/(Q\cap A))\\ &=\operatorname{ht}(Q'/Q)\\ &=\operatorname{ht}(Q')-\operatorname{ht}(Q), \end{align*} $$
where the first identity is because c is a codimension function, the second identity follows from the dimension formula [25, Tag 02IJ] as
![]() $A/I$
is universally catenary, and the third identity is because B is a catenary domain. Therefore,
$A/I$
is universally catenary, and the third identity is because B is a catenary domain. Therefore,
![]() $\delta (Q')=\delta (Q)$
. Since the pair
$\delta (Q')=\delta (Q)$
. Since the pair
![]() $(B,IB)$
is Henselian [25, Tag 09XK],
$(B,IB)$
is Henselian [25, Tag 09XK],
![]() $V(IB)$
is connected, see [25, Tag 09Y6]. Thus,
$V(IB)$
is connected, see [25, Tag 09Y6]. Thus,
![]() $\delta $
is a constant function on
$\delta $
is a constant function on
![]() $V(IB)$
. Therefore, for all maximal ideals
$V(IB)$
. Therefore, for all maximal ideals
![]() $\mathfrak {n}$
of B, which necessarily contains
$\mathfrak {n}$
of B, which necessarily contains
![]() $IB$
,
$IB$
,
![]() $\operatorname {ht}(\mathfrak {n})$
depends only on
$\operatorname {ht}(\mathfrak {n})$
depends only on
![]() $\mathfrak {n}\cap A$
, and thus must equal to
$\mathfrak {n}\cap A$
, and thus must equal to
![]() $\operatorname {ht}(\mathfrak {n}\cap A)$
. As discussed in Remark 6.7, we see A is universally catenary, as desired.
$\operatorname {ht}(\mathfrak {n}\cap A)$
. As discussed in Remark 6.7, we see A is universally catenary, as desired.
Proof of Theorem 8.4
Assume that A is I-adically complete,
![]() $A/I$
is a quotient of a Cohen–Macaulay ring, and
$A/I$
is a quotient of a Cohen–Macaulay ring, and
![]() $A/I$
is either quasi-excellent or semilocal and Nagata. Note that
$A/I$
is either quasi-excellent or semilocal and Nagata. Note that
![]() $(A,I)$
is a Henselian pair [25, Tag 0ALJ].
$(A,I)$
is a Henselian pair [25, Tag 0ALJ].
If
![]() $A/I$
is quasi-excellent, then A is quasi-excellent [Reference Kurano and Shimomoto15], in particular CM-quasi-excellent. If
$A/I$
is quasi-excellent, then A is quasi-excellent [Reference Kurano and Shimomoto15], in particular CM-quasi-excellent. If
![]() $A/I$
is semilocal and Nagata, then A is semilocal and Nagata [Reference Marot18], and thus has Cohen–Macaulay formal fibers by [Reference Takumi19, Theorem C]. Then A is CM-quasi-excellent, see [Reference Grothendieck8, Proposition 7.3.18]. Consequently, in both cases, A is CM-quasi-excellent.
$A/I$
is semilocal and Nagata, then A is semilocal and Nagata [Reference Marot18], and thus has Cohen–Macaulay formal fibers by [Reference Takumi19, Theorem C]. Then A is CM-quasi-excellent, see [Reference Grothendieck8, Proposition 7.3.18]. Consequently, in both cases, A is CM-quasi-excellent.
Now A satisfies condition (i) in Lemma 8.6 by the discussions in Remark 6.7, thus is universally catenary and admits a codimension function by Lemma 8.6. By Theorem 8.3, A is a quotient of a Cohen–Macaulay ring.
Acknowledgments
We thank Rankeya Datta, Longke Tang, and Kevin Tucker for helpful discussions. We thank Karl Schwede and Kevin Tucker for bringing the lifting problem of dualizing complexes to the author’s attention.