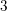 $3$-FOLDS IN CHARACTERISTIC
$3$-FOLDS IN CHARACTERISTIC 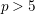 $p>5$
$p>5$Published online by Cambridge University Press: 10 September 2018
In this article, we prove a finiteness result on the number of log minimal models for 3-folds in 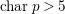 $\operatorname{char}p>5$. We then use this result to prove a version of Batyrev’s conjecture on the structure of nef cone of curves on 3-folds in characteristic
$\operatorname{char}p>5$. We then use this result to prove a version of Batyrev’s conjecture on the structure of nef cone of curves on 3-folds in characteristic 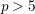 $p>5$. We also give a proof of the same conjecture in full generality in characteristic 0. We further verify that the duality of movable curves and pseudo-effective divisors hold in arbitrary characteristic. We then give a criterion for the pseudo-effectiveness of the canonical divisor
$p>5$. We also give a proof of the same conjecture in full generality in characteristic 0. We further verify that the duality of movable curves and pseudo-effective divisors hold in arbitrary characteristic. We then give a criterion for the pseudo-effectiveness of the canonical divisor 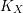 $K_{X}$ of a smooth projective variety in arbitrary characteristic in terms of the existence of a family of rational curves on
$K_{X}$ of a smooth projective variety in arbitrary characteristic in terms of the existence of a family of rational curves on 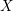 $X$.
$X$.