Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-27T02:44:32.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of the Quasiparticle Effective Masses in Semiconductors based on an Electron Self Energy Approach

Published online by Cambridge University Press:  16 February 2011

Xuejun Zhu ,
Mark S. Hybertsen  and
Steven G. Louie
Xuejun Zhu
Affiliation:
Department of Physics, University of California, and Materials and Chemical Sciences Division, Lawrence Berkeley Laboratory, Berkeley, CA 94720
Mark S. Hybertsen
Affiliation:
AT&T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974
Steven G. Louie
Affiliation:
Department of Physics, University of California, and Materials and Chemical Sciences Division, Lawrence Berkeley Laboratory, Berkeley, CA 94720
Get access

Abstract

A conceptually complete formalism for the quasiparticle effective masses in semiconductors is proposed. Our approach is based. on a generalized form of the 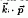theory, including the effects of the nonlocal, energy dependent electron self: energy operator Σ, which accounts for the electron-electron interaction. This introduces two -important effects on the expression of the effective mass: an explicit energy renormalization and an extra contribution to the matrix element that enters the usual . Our preliminary numerical results for prototypical GaAs show promising improvements over the results from the local density approximation for the calculated electron effective mass compared to experimental data.

Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 193: Symposium Q – Atomic Scale Calculations of Structure in Materials , 1990 , 113
Copyright
Copyright © Materials Research Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Hybertsen, M. S. and Louie, S. G., Comments on Cond. Matt. Phys 13, 223 (1987).Google Scholar
[2] Kane, E. O., in Semiconductors and Semimetals, ed. Willardson, R. K. and Beer, A. C. (Academic, 1966) Vol.1, p. 75.Google Scholar
[3] Kane, E. O, Phys. Rev. B 4, 1910 (1971).Google Scholar
[4] Landolt-Börnstein, Numerical Data and Functional Relationships in:Science and Technology, ed. Madelung, O., Vol. III 17a, Springer (1982).Google Scholar
[5] Hybertsen, M. S. and Louie, S. G., Phys. Rev. Lett. 55, 1418 (1985); Phys. Rev. B 34, 5390 (1986).Google Scholar
[6] Kane, E. O., J. Phys. Chem. Solids 6, 236 (1958).Google Scholar
[7] Levine, Z. H. and Allan, D. C., Phys. Rev. Lett. 63, 1719 (1990).Google Scholar
[8] Godby, R. W., Schliiter, M., and Sham, L. J., Phys. Rev. B 37, 10159 (1988); S. B. Zhang, et al, Phys. Rev. B 40, 3162 (1989).Google Scholar
[9] Levine, Z. H. and Louie, S. G., Phys. Rev. B:25, 6310 (1982).Google Scholar
[10] Hybertsen, M. S. and Louie, S. G., Phys. Rev. B 37, 2733 (1988), and X. Zhu and S. G. Louie, to be published.Google Scholar