Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T18:15:36.459Z Has data issue: false hasContentIssue false
  • English
  • Français

Redefinition of the formula for aldermanite, [Mg(H2O)6][Na(H2O)2Al3(PO4)2(OH,F)6]⋅H2O, and its crystal structure

Published online by Cambridge University Press:  14 April 2021

Peter Elliott ,
Ian E. Grey Open the ORCID record for Ian E. Grey [Opens in a new window]  and
Anthony C. Willis
Peter Elliott
Affiliation:
Department of Earth Sciences, School of Physical Sciences, The University of Adelaide, Adelaide 5005, South Australia, Australia South Australian Museum, North Terrace, Adelaide 5000, South Australia, Australia
Ian E. Grey*
Affiliation:
CSIRO Mineral Resources, Private Bag 10, Clayton South 3169, Victoria, Australia
Anthony C. Willis
Affiliation:
Research School of Chemistry, The Australian National University, Canberra, Australian Capital Territory 2601, Australia.
*
*Author for correspondence: Ian E. Grey, Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Aldermanite from Tom's quarry in the Kapunda–Angaston area of the Mount Lofty Ranges, South Australia has been characterised by electron microprobe analyses and single-crystal structure analysis. The empirical formula is Na0.72K0.13Ca0.06Mg1.15Al2.92(PO4)2.05[(OH)2.92F2.96]Σ5.88⋅8.91H2O, based on 23 anions. Analysis of a specimen from the type locality, the nearby Klemm's quarry, Moculta, gave a similar formula, Na0.59K0.06Ca0.36Mg0.92Al3.16(PO4)1.97[(OH)4.08F2.70]Σ6.78⋅8.36H2O. Na and F were not analysed in the original description of the mineral. The ideal end-member formula is [Mg(H2O)6][Na(H2O)2Al3(PO4)2(OH)6]⋅H2O, compared to the original formula of Mg5Al12(PO4)8(OH)22⋅nH2O with n ≈ 32. Aldermanite is monoclinic, P21/c with a = 13.524(3), b = 9.958(2), c = 7.013(1) Å and β = 97.40(3)°. The crystal structure of aldermanite is built from sawtooth layers of cis- and trans-corner-connected, Al-centred octahedra, decorated with corner-connected PO4 tetrahedra to give (100) layers of composition Al3(PO4)2(OH,F)6. Interlayer Mg(H2O)6 octahedra and H2O molecules hold the layers together through H bonding. The corner-connected octahedra form 6-membered rings that are centred by 8-coordinated Na and have a topology identical to a 3-octahedra-wide {110} slice of the pyrochlore structure. This pyrochlore element contains intersecting kagomé nets of Al atoms, parallel to (111) and (11$\bar{1}$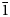) of cubic pyrochlore. Minerals of the walentaite group, as well as zirconolite-3O polytypes have the same type of intersecting kagomé nets of small cations.

Keywords

aldermanitecrystal structurestructural relationshipswalentaite-group mineralszirconolite-3Okagomé nets
Type
Article
Information
Mineralogical Magazine , Volume 85 , Issue 3 , June 2021 , pp. 348 - 353
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Mineralogical Society of Great Britain and Ireland

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Associate Editor: David Hibbs

References

Atencio, D., Andrade, M.B., Christy, A.G., Gieré, R. and Kartashov, P.M. (2010) The pyrochlore supergroup of minerals: nomenclature. The Canadian Mineralogist, 48, 673–698.10.3749/canmin.48.3.673CrossRefGoogle Scholar
Bayliss, P., Mazzi, F., Munno, R. and White, T.J. (1989) Mineral Nomenclature: zirconolite. Mineralogical Magazine, 53, 565–569.10.1180/minmag.1989.053.373.07CrossRefGoogle Scholar
Blount, A.M. (1974) The crystal structure of crandallite. American Mineralogist, 59, 41–47.Google Scholar
Chukanov, N.V., Zubkova, N.V., Pekov, I.V., Vigasina, M.F., Polekhovsky, Y.S., Ternes, B., Schüller, W., Britvin, S.N. and Pushcharovsky D.Yu. (2019) Stefanweissite, (Ca,REE)2Zr2(Nb,Ti)(Ti,Nb)2Fe2+O14, a new zirconolite-related mineral from the Eifel paleovolcanic region, Germany. Mineralogical Magazine, 83, 607–614.10.1180/mgm.2018.171CrossRefGoogle Scholar
Coppens, P. (1970) The evaluation of absorption and extinction in single-crystal structure analysis. Pp. 255−270 in: Crystallographic Computing (Ahmed, F.R., Hall, S.R. and Huber, C.P., editors). Munksgaard, Copenhagen.Google Scholar
Elliott, P., Peisley, V. and Mills, S.J. (2014) The phosphate deposits of South Australia. Australian Journal of Mineralogy, 17, 3–32.Google Scholar
Farrugia, L.J. (1999) WinGX suite for small-molecule single-crystal crystallography. Journal of Applied Crystallography, 32, 837–838.10.1107/S0021889899006020CrossRefGoogle Scholar
Gagné, O.C. and Hawthorne, F.C. (2015) Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Crystallographica, B71, 562–578.Google Scholar
Grey, I.E. (2020) Kagomé networks of octahedrally coordinated metal atoms in minerals. Relating different mineral structures through octahedral tilting. Mineralogical Magazine, 84, 640–652.10.1180/mgm.2020.72CrossRefGoogle Scholar
Grey, I.E., Mumme, W.G. and Hochleitner, R. (2019) Trimeric As3+3O6 clusters in walentaite: Crystal structure and revised formula. European Journal of Mineralogy, 31, 111–116.10.1127/ejm/2018/0030-2790CrossRefGoogle Scholar
Grey, I.E., Hochleitner, R., Rewitzer, C., Riboldi-Tunnicliffe, A., Kampf, A.R., MacRae, C.M., Mumme, W.G., Kaliwoda, M., Friis, H. and Martin, C.U. (2020) The walentaite group and the description of a new member, alcantarillaite, from the Alcantarilla mine, Belalcazar, Cordoba, Andalusia, Spain. Mineralogical Magazine, 84, 412−419.10.1180/mgm.2020.18CrossRefGoogle Scholar
Harrowfield, I.R., Segnit, E.R. and Watts, J.A. (1981) Aldermanite, a new magnesium aluminium phosphate. Mineralogical Magazine, 44, 59−62.10.1180/minmag.1981.44.333.08CrossRefGoogle Scholar
Magneli, A. (1952) Tungsten bronzes containing six-membered rings of WO3 octahedra. Nature, 169, 791−792.10.1038/169791a0CrossRefGoogle Scholar
Miyawaki, R., Hatert, F., Pasero, M. and Mills, S.J. (2021) IMA Commission on New Minerals, Nomenclature and Classification (CNMNC) − Newsletter 60. Mineralogical Magazine, 85, https://doi.org/10.1180/mgm.2021.30Google Scholar
Otwinowski, Z., Borek, D., Majewski, W. and Minor, W. (2003) Multiparametric scaling of diffraction intensities. Acta Crystallographica, A59, 228−234.10.1107/S0108767303005488CrossRefGoogle Scholar
Petříček, V., Dušek, M. and Palatinus, L. (2014) Crystallographic Computing System JANA2006: General features. Zeitschrift für Kristalloraphie, 229, 345–352.Google Scholar
Pouchou, J.L. and Pichoir, F. (1985) “PAP” φ(ρZ) procedure for improved quantitative microanalysis. Pp. 104−106 in: Microbeam Analysis (Armstrong, J.T., editor). San Francisco Press, California, USA.Google Scholar
Sheldrick, G.M. (2008) A short history of SHELX. Acta Crystallographica, A64, 112−122.10.1107/S0108767307043930CrossRefGoogle Scholar
Subramanian, M.A., Aravamudan, G. and Subba Rao, G.V. (1983) Oxide pyrochlores − a review. Progress in Solid State Chemistry, 15, 55–143.10.1016/0079-6786(83)90001-8CrossRefGoogle Scholar
Syôzi, I. (1951) Statistics of kagomé lattice. Progress of Theoretical Physics, VI, 306–308.10.1143/ptp/6.3.306CrossRefGoogle Scholar
Supplementary material: File

Grey et al. supplementary material

Grey et al. supplementary material 1

Download Grey et al. supplementary material(File)
File 30.2 KB
Supplementary material: File

Grey et al. supplementary material

Grey et al. supplementary material 2

Download Grey et al. supplementary material(File)
File 132.3 KB