If E1 and E2 are subsets of ℝn and a- is an isometry or similarity transformation, it is useful to be able to estimate the Hausdorff dimension of E1 ∩ σ(E2) in terms of the dimensions of E1 and E2. If E1 and E2 are compact, then, as σvaries, dim (El ∩ σ(E2)) is “in general” at most max (dim E1 + dim E2 − n, 0) and “often” at least this value (see Mattila [9] and Kahane [7] for more precise statements of these ideas). However, as we shall see, it is possible to construct non-compact sets E of any given dimension that are “sufficiently dense” in ℝn to ensure that dim (E ∩ σ(E)) = dim E for all similarities σ More generally, we shall show that for each s there are large classes of sets & of dimensions between s and n, closed under reasonable transformations including similarities, such that the intersection of any countable collection of sets in & has dimension at least s. Such collections of sets are required, for example, in the constructions of subsets of ℝn with certain dimensional properties given by Davies [1] and Falconer [5].

We show that if a polytope K1, in ℝd can be partitioned into a finite number of sets, and these sets can be moved by isometries in a locally discrete group to form a convex body K2, then K2 is a polytope and a similar partition can be made where the sets involved are simplices with disjoint interiors. This gives partial answers to questions of Tarski, Sallee and Wagon.

We consider a tiling of a square with convex tiles of areas a1,… aN and perimeters p1,…,pN and pose the following problems.

PROBLEM 1. For given values of a1, …, aN find the minimum of P = p1 + … + pN.

PROBLEM 2. For given values of p1,…,pN find the maximum of A = a1+…+aN.

If E is a subset of ℝn (n ≥ 1) we define the distance set of E as

The best known result on distance sets is due to Steinhaus [11], namely, that, if E ⊂ ℝn is measurable with positive n-dimensional Lebesgue measure, then D(E) contains an interval [0, ε) for some ε > 0. A number of variations of this have been examined, see Falconer [6, p. 108] and the references cited therein.

We shall consider incomplete exponential sums of the shape

where q, a and h are integers satisfying 1 ≤ a < a + h ≤ q, f(x) is a function denned at least for the integers in the range of summation, and eq(t) is an abbreviation for e2πit/q.

Let A and B be Borel (or more generally Suslin) sets in ℝn whose Hausdorff dimensions satisfy

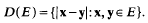
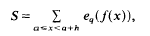
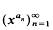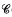
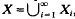It is proved that the sequence is completely uniformly distributed modulo 1 for almost all real numbers x with |x|> 1, if (an) is an arbitrary sequence of distinct positive integers.

Le point de départ de ce travail est le résultat suivant.

THÉORÈME (I. Namioka). Soient X et Y deux espaces compacts et

Si f est continue quand on munit(Y) de la topologie de convergence simple alors X contient un Gδ dense en tout point duquel f reste continue quand on munit(Y) de la topologie de la convergence uniform.

In [8,9] Jayne and Rogers studied piece-wise closed maps and ℱσ maps between metric spaces. A map f of a metric space X into a metric space Y is said to be an ℱσ map if: (a) f maps ℱσ-sets in X to ℱσ-sets in Y; and (b) f1 maps ℱσ-sets in Y back to ℱσ-sets in X. 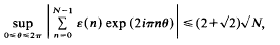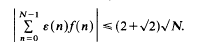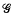A map fof a metric space X into a metric space Y is said to be piece-wise closed if:it is possible to find a sequence X1, X2,… of closed sets in X, with with each setf(Xi), i ≥ 1, closed in Y, and with the restriction offto each Xi, a closed map (i.e., a continuous map that maps closed sets to closed sets).

Extending the well-known property of the Rudin- Shapiro sequence ε = (ε(n)) with values in {−1, +1} satisfying

we show that for all unimodular 2-multiplicative sequences f = (f(n))

Let be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point z0 in Δ we can evaluate all matrix entries of at z0, to obtain a subgroup {z0} of SL (2, ℂ) and a surjective representation → {z0}. If this representation is not faithful, then contains a nontrivial element W such that W evaluated; at z0 is trivial. But W can evaluate to the identity only on a countable subset) of Δ, and there are only countably many choices for W in Consequently there are at most countably many points zk in Δ such that {zk} is not isomorphic to Δ. Our main result can now be stated as follows.

In the middle of the last century, Kummer's studies on the famous Fermat conjecture led him to the question: when does a given prime p > 2 divide the class number of the p-th cyclotomic field? His conclusion was that this happens, if, and only if, p divides at least one of the Bernoulli numbers B2, B4,…, Bp_3. Such a prime is called irregular. Carlitz [1] has given the simplest proof of the fact that the number of irregular primes is infinite. However, it is not known whether there are infinitely many regular primes.

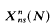Let . denote the modular curve associated with the normalizer of a non-split Cartan group of level 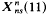N., where N. is an arbitrary integer. The curve is denned over Q and the corresponding scheme over ℤ[1/N] is smooth [1]. If N. is a prime, the genus formula for . is given in [5,6]. The curve . has genus 0 if N < 11 and has genus 1. Ligozat [5] has shown that the group of Q-rational points on has rank 1. If the genus g(N). is greater than 1, very little is known about the Q-rational points of . Since under simple conditions imaginary quadratic fields with class number 1 give an integral point on these curves, Serre and others have asked whether all integral points are obtained in this way [8].

We use the Buchstab-Rosser sieve to derive an asymptotic formula for the distribution of those integers n for which the r numbers n + l1, n + l2,…, n + lr are all square-free. Our error estimate sharpens a similar result of Hall and is uniform in both r and maxl 1≤i≤r|li|.

The work to be described here, with the fruit of previous investigations in [1] and [2], yields the following general theorem.

In this paper we study certain properties of free actions of non-abelian p-groups (p≥3) on products of spheres (Sn)k, k≥2. The following theorems are proved.

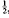Recently, Szczepariski [11] has constructed examples of aspherical manifolds with the ℚ-homology of a sphere. More precisely, if k is a commutative ring of characteristic zero containing , the following theorem holds.

We consider two additive cubic equations

in p-adic fields. Davenport and Lewis showed that the equations have a non-trivial solution in every p-adic field, if n ≥ 16, and need not have a solution in the 7-adic field, if n = 15. Here we prove that if p ≠ 7 the equations have a non-trivial solution in p-adic fields if n ≥ 13. When n = 12 such a result fails for every prime p ≡ 1 (mod 3).

The results we present were motivated by the product measure problem for Baire measures. For two completely regular Hausdorff spaces X and Y, with totally finite a- additive measures μ and ν defined on the Baire σ- algebras ℬ0(X) and ℬ0(Y) respectively, under what conditions may we define a measure λ on the Baire σ-algebra ℬ0(X × Y), extending the product measure μ ⊗ ν defined on the product σ-algebra ℬ0(X) × ℬ0(Y) and satisfying a Fubini theorem?

Suppose that θ is a positive irrational number and α is an arbitrary real number. Then Kronecker's Theorem in diophantine approximation (Theorem 440 of [7[) can be stated as follows.