Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barberis, Maria L.
Dotti Miatello, Isabel G.
and
Miatello, Roberto J.
1995.
On certain locally homogeneous Clifford manifolds.
Annals of Global Analysis and Geometry,
Vol. 13,
Issue. 3,
p.
289.
Rossetti, J.
and
Tirao, P.
1996.
Compact flat manifolds with holonomy group 𝐙₂⊕𝐙₂.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 8,
p.
2491.
Miatello, R. J.
and
Rossetti, J. P.
2001.
Flat manifolds isospectral on p-forms.
Journal of Geometric Analysis,
Vol. 11,
Issue. 4,
p.
649.
Dotti, Isabel G.
and
Miatello, Roberto J.
2001.
Quaternion Kähler flat manifolds.
Differential Geometry and its Applications,
Vol. 15,
Issue. 1,
p.
59.
Tirao, Paulo
2001.
Primitive compact flat manifolds with holonomy groupZ2 ⊕ Z2.
Pacific Journal of Mathematics,
Vol. 198,
Issue. 1,
p.
207.
Console, S.
Miatello, R.J.
and
Rossetti, J.P.
2010.
Z2-cohomology and spectral properties of flat manifolds of diagonal type.
Journal of Geometry and Physics,
Vol. 60,
Issue. 5,
p.
760.


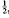 , the following theorem holds.
, the following theorem holds.