Research Article
A note on successive approximation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
-
- Article
- Export citation
Polynomials with multiple zeros
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 181-196
-
- Article
- Export citation
The connectivity function of a graph
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-202
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (II)
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-107
-
- Article
- Export citation
On the realization of distances within coverings of an n-sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-206
-
- Article
- Export citation
On the Hankel determinants of univalent functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-112
-
- Article
- Export citation
Front matter
MTK volume 14 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Research Article
Double covering with spheres
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 207-214
-
- Article
- Export citation
On the finite deformation of inhomogeneous elastic materials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 215-219
-
- Article
- Export citation
Linear forms in the logarithms of algebraic numbers (III)
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 220-228
-
- Article
- Export citation
Corrigendum and addendum
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 229-232
-
- Article
- Export citation
Index
Index to volume 14
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 233
-
- Article
- Export citation
Front matter
MTK volume 14 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

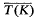 of
of 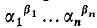 is transcendental.
is transcendental.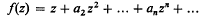
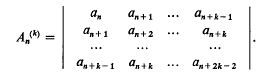
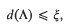
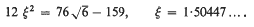
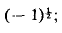 of each particle
of each particle