Research Article
Approximate subdifferentials and applications 3: the metric theory
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-38
-
- Article
- Export citation
Tangential Limits for Certain Classes of Analytic Functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-49
-
- Article
- Export citation
Stability in the Aleksandrov-Fenchel-Jessen Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 50-59
-
- Article
- Export citation
On Integer Sets Containing Strings of Consecutive Integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 60-70
-
- Article
- Export citation
On Negative Moments of the Riemann Zeta-Function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-88
-
- Article
- Export citation
On p-Class Groups of Cyclic Extensions of Prime Degree p of Quadratic Fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-102
-
- Article
- Export citation
An analytical bound on the asymmetry of a section of a typical three-dimensional brownian path
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-106
-
- Article
- Export citation
On -complete filters
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-115
-
- Article
- Export citation
On inductive limits of measure spaces and projective limits of Lp-spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-130
-
- Article
- Export citation
Ramsey type theorems for real functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-141
-
- Article
- Export citation
Shadow boundaries of typical convex bodies. measure properties
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
-
- Article
- Export citation
The viscous flow through symmetric collapsible channels
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-181
-
- Article
- Export citation
Book Reviews
Book Reviews - B. J. Alder, Editor. Special Purpose Computers. Academic Press. 1988, 282 pp., $49.95. - D. R. Bland. Wave Theory and Applications. Clarendon Press. 1988, 317 pp., hardback £40, paperback £.15. - S. Caenepeel and F. Van Oystaeyen Brauer Groups and the Cohomology of Graded Rings. Marcel Dekker. 1988, 261 pp., 107.50. - G. F. Carrier and C. E. Pearson. Partial Differential Equations Theory and Technique. Academic Press. 1988, 340 pp., $39.95. - D. V. Chudnovsky and G. V. Chudnovsky Editors. Search Theory: Some Recent Developments. Marcel Dekker. 1989, 155 pp., $107.50. - R. Durrett. Lecture Notes on Particle Systems and Percolation. Wadsworth & Brooks/Cole. 1988, 335 pp., $39.95. - D. H. Griffel Linear Algebra and its Applications: Volume 1, A First Course. Ellis Horwood. 1989, 289 pp., £16.95. - S. P. Gudder. Quantum Probability. Academic Press. 1988, 316 pp., $49.50. - M. Hervé. Several Complex Variables: Local Theory, 2nd Edition. Oxford University Press. 1987, 148 pp., £8.95. - K. Ito and N. Ikeda, Editors. Probabilistic Methods in Mathematical Physics; Proceedings of the Katata and Kyoto Symposia: 1985. Academic Press.1988, 441 pp., $59.50. - G. Karpilovsky. Field theory: Classical Foundations and Multiplicative Groups. Marcel Dekker. 1988, 550 pp., $119.50. - P. Pelcé Editor. Dynamics of Curved Fronts. Academic Press. 1988, 514 pp., $69.50. - G. Sewell. The Numerical Solution of Ordinary and Partial Equations. Academic Press. 1988, 271 pp., $39.95. - J. S. Walker. Fourier Analysis. Oxford University Press. 1988, 440 pp., £40. - N. R. Wallach. Real Reductive Groups I. Academic Press. 1988, 412 pp., $59.95. - W. D. Wallis. Combinatorial Designs. Marcel Dekker. 1988, 323 pp., $107.50. - W. Wieslaw. Topological Fields. Marcel Dekker. 1988, 309 pp., $119.50.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-185
-
- Article
- Export citation
Front matter
MTK volume 36 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation


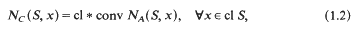
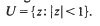
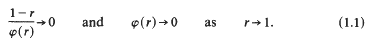
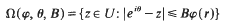
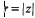 The region . makes tangential contact with the boundary
The region . makes tangential contact with the boundary 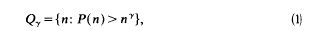
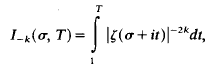
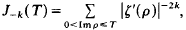
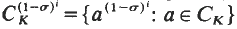 for
for 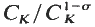 is an elementary abelian
is an elementary abelian 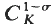 . We let
. We let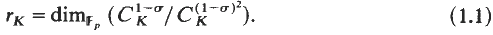
 , ) is the inductive limit of the measure spaces (
, ) is the inductive limit of the measure spaces (