Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rockett, Andrew M.
and
Sz�sz, Peter
1993.
On tangential regions for power series.
Archiv der Mathematik,
Vol. 60,
Issue. 5,
p.
446.
Twomey, J. B.
1997.
Radial variation of functions in Dirichlet‐type spaces.
Mathematika,
Vol. 44,
Issue. 2,
p.
267.
Girela, Daniel
and
Peláez, José Ángel
2006.
Boundary behaviour of analytic functions in spaces of Dirichlet type.
Journal of Inequalities and Applications,
Vol. 2006,
Issue. ,
p.
1.
Sun, Cecilia
2007.
Resisting the airport: Bang on a can performs Brian Eno.
Musicology Australia,
Vol. 29,
Issue. 1,
p.
135.
MacGregor, Thomas H.
and
Sterner, Michael P.
2018.
Boundary limits of fractional derivatives of univalent functions.
Complex Variables and Elliptic Equations,
Vol. 63,
Issue. 11,
p.
1529.


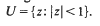
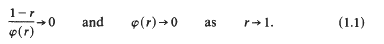
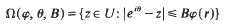
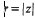 The region . makes tangential contact with the boundary
The region . makes tangential contact with the boundary 