Research Article
The mean value theorem for the Riemann zeta-function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 177-184
-
- Article
- Export citation
On the functional equations satisfied by modular functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-190
-
- Article
- Export citation
A classifying space for the contact pseudogroup
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 191-201
-
- Article
- Export citation
Measures of Hausdorff type and stable processes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 202-212
-
- Article
- Export citation
On the representation of increasing linear functionals on Riesz spaces by measures
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-215
-
- Article
- Export citation
The effect of distant sidewalls on the transition to finite amplitude Bénard convection—II
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-235
-
- Article
- Export citation
A cyclotomic construction for Leech's lattice
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 236-241
-
- Article
- Export citation
J-fields generated by roots of cyclotomic integers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 242-250
-
- Article
- Export citation
The centralizer poset in groups of semilinear maps
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-263
-
- Article
- Export citation
Sets homothetic to intersections of their translates
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 264-269
-
- Article
- Export citation
Isometries of the space of convex bodies of Ed
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-278
-
- Article
- Export citation
Isomorphic factorisations V: Directed graphs
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-285
-
- Article
- Export citation
Index
Index to volume 25
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 286
-
- Article
- Export citation
Front matter
MTK volume 25 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

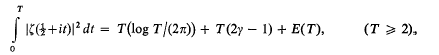



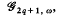 the contact pseudogroup. Passing to germs of local diffeomorphisms we obtain a topological groupoid Γ
the contact pseudogroup. Passing to germs of local diffeomorphisms we obtain a topological groupoid Γ