Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T19:51:27.642Z Has data issue: false hasContentIssue false
  • English
  • Français

A SIMPLICIAL POLYTOPE THAT MAXIMIZES THE ISOTROPIC CONSTANT MUST BE A SIMPLEX

Part of: Optimality conditions Metric geometry General convexity

Published online by Cambridge University Press:  22 May 2015

Luis Rademacher
Luis Rademacher*
Affiliation:
Computer Science and Engineering, The Ohio State University, U.S.A. email [email protected]
Get access

Abstract

The isotropic constant 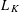$L_{K}$ is an affine-invariant measure of the spread of a convex body 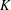$K$. For a 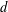$d$-dimensional convex body 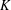$K$, 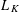$L_{K}$ can be defined by 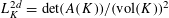$L_{K}^{2d}=\det (A(K))/(\text{vol}(K))^{2}$, where 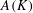$A(K)$ is the covariance matrix of the uniform distribution on 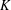$K$. It is an open problem to find a tight asymptotic upper bound of the isotropic constant as a function of the dimension. It has been conjectured that there is a universal constant upper bound. The conjecture is known to be true for several families of bodies, in particular, highly symmetric bodies such as bodies having an unconditional basis. It is also known that maximizers cannot be smooth. In this work we study bodies that are neither smooth nor highly symmetric by showing progress towards reducing to a highly symmetric case among non-smooth bodies. More precisely, we study the set of maximizers among simplicial polytopes and we show that if a simplicial polytope 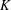$K$ is a maximizer of the isotropic constant among 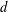$d$-dimensional convex bodies, then when 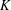$K$ is put in isotropic position it is symmetric around any hyperplane spanned by a 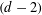$(d-2)$-dimensional face and the origin. By a result of Campi, Colesanti and Gronchi, this implies that a simplicial polytope that maximizes the isotropic constant must be a simplex.

MSC classification

Primary: 52A23: Asymptotic theory of convex bodies
Secondary: 52A40: Inequalities and extremum problems 49K30: Optimal solutions belonging to restricted classes 51F15: Reflection groups, reflection geometries
Type
Research Article
Information
Mathematika , Volume 62 , Issue 1 , 2016 , pp. 307 - 320
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, K., Logarithmically concave functions and sections of convex sets in Rn. Studia Math. 88(1) 1988, 69–84.CrossRefGoogle Scholar
Barthe, F. and Fradelizi, M., The volume product of convex bodies with many hyperplane symmetries. Amer. J. Math. 135(2) 2013, 311–347.CrossRefGoogle Scholar
Bourgain, J., On high-dimensional maximal functions associated to convex bodies. Amer. J. Math. 108(6) 1986, 1467–1476.CrossRefGoogle Scholar
Brazitikos, S., Giannopoulos, A., Valettas, P. and Vritsiou, B.-H., Geometry of Isotropic Convex Bodies (Mathematical Surveys and Monographs 196), American Mathematical Society (Providence, RI, 2014).CrossRefGoogle Scholar
Campi, S., Colesanti, A. and Gronchi, P., A note on Sylvester’s problem for random polytopes in a convex body. Rend. Istit. Mat. Univ. Trieste 31(1–2) 1999, 79–94.Google Scholar
Feller, W., An Introduction to Probability Theory and its Applications, 2nd edn, Vol. II, John Wiley & Sons (New York, 1971).Google Scholar
Giannopoulos, A., Notes on isotropic convex bodies. http://www.math.uoc.gr/∼apostolo/isotropic-bodies.ps, October 2003.Google Scholar
Giannopoulos, A. A., On the mean value of the area of a random polygon in a plane convex body. Mathematika 39(2) 1992, 279–290.CrossRefGoogle Scholar
Klartag, B., On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16(6) 2006, 1274–1290.CrossRefGoogle Scholar
Koldobsky, A., Fourier Analysis in Convex Geometry (Mathematical Surveys and Monographs 116), American Mathematical Society (Providence, RI, 2005).CrossRefGoogle Scholar
Meyer, M., Une caractérisation volumique de certains espaces normés de dimension finie. Israel J. Math. 55(3) 1986, 317–326.CrossRefGoogle Scholar
Milman, V. D. and Pajor, A., Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. In Geometric Aspects of Functional Analysis (1987–88) (Lecture Notes in Mathematics 1376), Springer (Berlin, 1989), 64–104.CrossRefGoogle Scholar
Rademacher, L., On the monotonicity of the expected volume of a random simplex. Mathematika 58(1) 2012, 77–91.CrossRefGoogle Scholar
Reisner, S., Schütt, C. and Werner, E. M., Mahler’s conjecture and curvature. Int. Math. Res. Not. IMRN 2012(1) 2012, 1–16.CrossRefGoogle Scholar
Rockafellar, R. T., Convex Analysis, Princeton University Press (Princeton, NJ, 1970).CrossRefGoogle Scholar
Saint-Raymond, J., Sur le volume des corps convexes symétriques. In Initiation Seminar on Analysis, 20th Year: 1980/1981 (Publ. Math. Univ. Pierre et Marie Curie 46), University Paris VI (Paris, 1981), Exp. No. 11.Google Scholar
Saroglou, C., Characterizations of extremals for some functionals on convex bodies. Canad. J. Math. 62(6) 2010, 1404–1418.CrossRefGoogle Scholar
Schechtman, G. and Zinn, J., On the volume of the intersection of two L pn balls. Proc. Amer. Math. Soc. 110(1) 1990, 217–224.Google Scholar
Schneider, R., Convex Bodies: The Brunn-Minkowski Theory (Encyclopedia of Mathematics and its Applications 44), Cambridge University Press (Cambridge, 1993).CrossRefGoogle Scholar
Stancu, A., Two volume product inequalities and their applications. Canad. Math. Bull. 52(3) 2009, 464–472.CrossRefGoogle Scholar
Ziegler, G. M., Lectures on Polytopes (Graduate Texts in Mathematics 152), Springer (New York, 1995).CrossRefGoogle Scholar